por ·Sin comentarios

Introducción

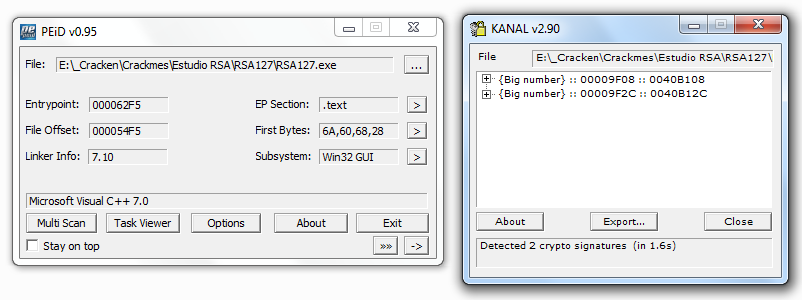
Segunda crackme con RSA que afrontamos. Esta vez se trata de un crackme realizado en VC++ 7.0 y en sus entrañas utiliza RSA-127. Una cosa que no comenté en la entrega anterior (RSA-200), es que conviene utilizar el plugin Kanal de PEiD para localizar cuando se utilizan números grandes o determinados hashes como MD5 o SHA1.

16-02-2015 01-49-36

Otra cosa es que os quería comentar es la coletilla 127. Esta lo determina el módulo n e indica el número de bits de éste.

Funcionamiento de RSA

  1. Inicialmente es necesario generar aleatoriamente dos números primos grandes, a los que llamaremos p y q.
  2. A continuación calcularemos n como producto de p y q: 
    n = p * q
  3. Se calcula fi: 
    fi(n)=(p-1)(q-1)
  4. Se calcula un número natural e de manera que MCD(e, fi(n))=1 , es decir e debe ser primo relativo de fi(n). Es lo mismo que buscar un numero impar por el que dividir fi(n) que de cero como resto.
  5. Mediante el algoritmo extendido de Euclides se calcula d que es el inverso modular de e. 
    Puede calcularse d=((Y*fi(n))+1)/e para Y=1,2,3,... hasta encontrar un d entero.
  6. El par de números (e,n) son la clave pública.
  7. El par de números (d,n) son la clave privada.
  8. Cifrado: La función de cifrado es. 
    c = m^e mod n
  9. Descifrado: La función de descifrado es. 
    m = c^d mod n

OllyDbg

Con OllyDbg analizamos la parte del código que nos interesa.

0040109B    .  68 00010000         PUSH 100                                  ; /Count = 100 (256.)
004010A0    .  52                  PUSH EDX                                  ; |Buffer = RSA127.<ModuleEntryPoint>
004010A1    .  68 EA030000         PUSH 3EA                                  ; |ControlID = 3EA (1002.)
004010A6    .  8B8C24 28020000     MOV ECX,DWORD PTR SS:[ESP+228]            ; |
004010AD    .  51                  PUSH ECX                                  ; |hWnd = NULL
004010AE    .  FF15 F0B04000       CALL DWORD PTR DS:[<&USER32.GetDlgItemTex>; \GetDlgItemTextA
004010B4    .  8D5424 04           LEA EDX,DWORD PTR SS:[ESP+4]
004010B8    .  57                  PUSH EDI
004010B9    .  52                  PUSH EDX                                  ;  RSA127.<ModuleEntryPoint>
004010BA    .  50                  PUSH EAX                                  ;  kernel32.BaseThreadInitThunk
004010BB    .  E8 201E0000         CALL RSA127.00402EE0
004010C0    .  83C4 0C             ADD ESP,0C
004010C3    .  8D9424 04010000     LEA EDX,DWORD PTR SS:[ESP+104]
004010CA    .  68 00010000         PUSH 100                                  ; /Count = 100 (256.)
004010CF    .  52                  PUSH EDX                                  ; |Buffer = RSA127.<ModuleEntryPoint>
004010D0    .  68 EB030000         PUSH 3EB                                  ; |ControlID = 3EB (1003.)
004010D5    .  8B8C24 28020000     MOV ECX,DWORD PTR SS:[ESP+228]            ; |
004010DC    .  51                  PUSH ECX                                  ; |hWnd = NULL
004010DD    .  FF15 F0B04000       CALL DWORD PTR DS:[<&USER32.GetDlgItemTex>; \GetDlgItemTextA
004010E3    .  8D9424 04010000     LEA EDX,DWORD PTR SS:[ESP+104]
004010EA    .  52                  PUSH EDX                                  ;  RSA127.<ModuleEntryPoint>
004010EB    .  8B4C24 04           MOV ECX,DWORD PTR SS:[ESP+4]
004010EF    .  51                  PUSH ECX
004010F0    .  E8 5B1F0000         CALL RSA127.00403050
004010F5    .  68 08B14000         PUSH RSA127.0040B108                      ;  ASCII "666AAA422FDF79E1D4E41EDDC4D42C51"
004010FA    .  55                  PUSH EBP
004010FB    .  E8 501F0000         CALL RSA127.00403050
00401100    .  68 2CB14000         PUSH RSA127.0040B12C                      ;  ASCII "29F8EEDBC262484C2E3F60952B73D067"
00401105    .  56                  PUSH ESI
00401106    .  E8 451F0000         CALL RSA127.00403050
0040110B    .  53                  PUSH EBX
0040110C    .  55                  PUSH EBP
0040110D    .  56                  PUSH ESI
0040110E    .  8B5424 24           MOV EDX,DWORD PTR SS:[ESP+24]
00401112    .  52                  PUSH EDX                                  ;  RSA127.<ModuleEntryPoint>
00401113    .  E8 38250000         CALL RSA127.00403650
00401118    .  53                  PUSH EBX
00401119    .  57                  PUSH EDI
0040111A    .  E8 31130000         CALL RSA127.00402450
0040111F    .  83C4 30             ADD ESP,30
00401122    .  85C0                TEST EAX,EAX                              ;  kernel32.BaseThreadInitThunk
00401124    .  74 12               JE SHORT RSA127.00401138
00401126    .  B8 01000000         MOV EAX,1
0040112B    .  81C4 08020000       ADD ESP,208
00401131    .  5B                  POP EBX                                   ;  kernel32.7590EE1C
00401132    .  5D                  POP EBP                                   ;  kernel32.7590EE1C
00401133    .  5E                  POP ESI                                   ;  kernel32.7590EE1C
00401134    .  5F                  POP EDI                                   ;  kernel32.7590EE1C
00401135    .  C2 1000             RETN 10
00401138    >  6A 40               PUSH 40                                   ; /Style = MB_OK|MB_ICONASTERISK|MB_APPLMODAL
0040113A    .  68 5CB14000         PUSH RSA127.0040B15C                      ; |Title = "Yeah!"
0040113F    .  68 50B14000         PUSH RSA127.0040B150                      ; |Text = "Nice job!!!"
00401144    .  6A 00               PUSH 0                                    ; |hOwner = NULL
00401146    .  FF15 F4B04000       CALL DWORD PTR DS:[<&USER32.MessageBoxA>] ; \MessageBoxA

El código nos proporciona el exponente público (e) y el módulo (n).

  • e = 29F8EEDBC262484C2E3F60952B73D067
  • n = 666AAA422FDF79E1D4E41EDDC4D42C51

Finalmente realiza un PowMod con el número de serie del disco C y el par de claves (e,n).

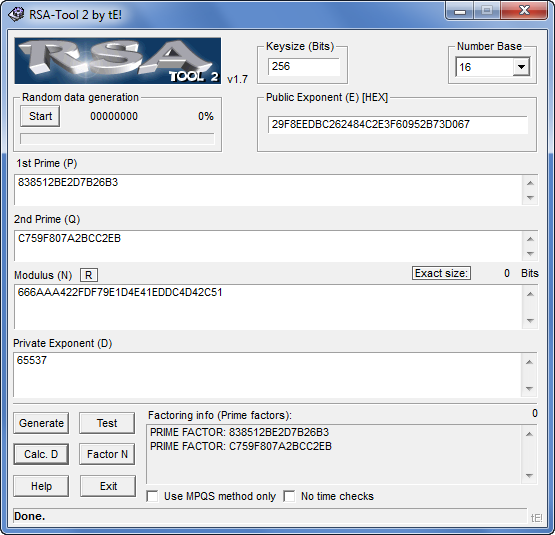
Calculando la clave privada (d)

Una vez localizados los datos anteriores lo siguiente es factorizar para obtener los primos p y q y finalmente d.

RSA127_rsatool

d = 65537

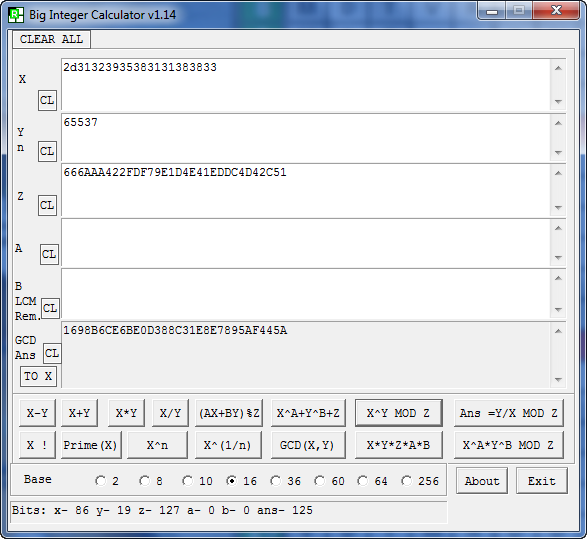
Ejemplo operacional

Nº serie disco C = -1295811883
Serial = hdd.getBytes()^d mod n
Serial = 2d31323935383131383833^65537 mod 666AAA422FDF79E1D4E41EDDC4D42C51
Serial = 1698B6CE6BE0D388C31E8E7895AF445A

RSA127_bigint

Keygen

El keygen está hecho en Java ya que permite trabajar con números grandes de forma sencilla.

JButton btnNewButton = new JButton("Generar");
        btnNewButton.addActionListener(new ActionListener() {
            public void actionPerformed(ActionEvent arg0) {
                BigInteger serial = new BigInteger("0");
                BigInteger n = new BigInteger("136135092290573418981810449482425576529");
                BigInteger d = new BigInteger("415031");
                String hdd = t1.getText();
                BigInteger tmp = new BigInteger(hdd.getBytes());
                serial = tmp.modPow(d, n);
                t2.setText(serial.toString(16).toUpperCase());
            }
        });

Links

Cruehead’s Crackme 2.0 Serial [2/3]
Introducción Continuamos con la segunda entrega de Cruehead. En este caso nos encontramos con un único campo de contraseña para
Solución al Time Trial de Detten
Intro Hoy tenemos aquí otro crackme sacado del baúl de los recuerdos. En este caso se trata de una protección
Challengeland.co Realistic 1
Alerta de Spoiler: El reto está en activo a fecha de publicación. Spoiler alert: The challenge is still alive. Este
Keygen para el Crackme 1 de VisionZ
Intro Aquí tenemos un crackme clásico realizado en Visual C++. La única particularidad que tiene es que no muestra MessageBox

por ·2 comentarios

Introducción

Continuamos con la segunda entrega de Cruehead. En este caso nos encontramos con un único campo de contraseña para introducir.

El algoritmo

Abrimos con Olly y vemos dos saltos. El primer Call realiza una serie de operaciones con el serial introducido y el segundo comprueba si el serial es correcto.

01

A continuación llegamos aquí:

00401365     /$  C605 18214000 00         MOV BYTE PTR DS:[402118],0
0040136C     |.  8B7424 04                MOV ESI,DWORD PTR SS:[ESP+4]
00401370     |.  56                       PUSH ESI
00401371     |>  8A06                     /MOV AL,BYTE PTR DS:[ESI]      ; <---
00401373     |.  84C0                     |TEST AL,AL
00401375     |.  74 19                    |JE SHORT CRACKME2.00401390
00401377     |.  FE05 18214000            |INC BYTE PTR DS:[402118]
0040137D     |.  3C 41                    |CMP AL,41                     ; 41 = A
0040137F     |.  72 04                    |JB SHORT CRACKME2.00401385    ; ya es mayúscula
00401381     |.  3C 5A                    |CMP AL,5A                     ; 5A = Z
00401383     |.  73 03                    |JNB SHORT CRACKME2.00401388   ; Convertir a mayúscula
00401385     |>  46                       |INC ESI
00401386     |.^ EB E9                    |JMP SHORT CRACKME2.00401371   ; Bucle -->
00401388     |>  E8 25000000              |CALL CRACKME2.004013B2
0040138D     |.  46                       |INC ESI
0040138E     |.^ EB E1                    \JMP SHORT CRACKME2.00401371
00401390     |>  5E                       POP ESI
00401391     |.  E8 03000000              CALL CRACKME2.00401399         ;Convertido a mayúsculas continuamos
00401396     |.  EB 00                    JMP SHORT CRACKME2.00401398
00401398     \>  C3                       RETN

Si nuestro serial contiene solo letras, las convierte a mayúsculas y seguimos aquí. En resumen hace XOR byte a byte entre nuestro serial y la frase «Messing_in_bytes»

00401399     /$  33DB                     XOR EBX,EBX
0040139B     |.  33FF                     XOR EDI,EDI
0040139D     |>  8A8F A3214000            /MOV CL,BYTE PTR DS:[EDI+4021A3]  ; Carga el primer byte de 4021A3
004013A3     |.  8A1E                     |MOV BL,BYTE PTR DS:[ESI]         ;
004013A5     |.  84DB                     |TEST BL,BL
004013A7     |.  74 08                    |JE SHORT CRACKME2.004013B1
004013A9     |.  32D9                     |XOR BL,CL                        ; byteSerial XOR Byte"Messing_in..."
004013AB     |.  881E                     |MOV BYTE PTR DS:[ESI],BL
004013AD     |.  46                       |INC ESI                          ;Siguiente byte de "Messing_in_bytes"
004013AE     |.  47                       |INC EDI                          ;Siguiente byte del serial
004013AF     |.^ EB EC                    \JMP SHORT CRACKME2.0040139D
004013B1     \>  C3                       RETN                              ;XOR finalizado volvemos

Estado del DUMP (memoria) antes del XOR y con nuestro serial (12345678) cargado.

00402118  00 47 6F 6F 64 20 77 6F 72 6B 21 00 47 72 65 61  .Good work!.Grea
00402128  74 20 77 6F 72 6B 2C 20 6D 61 74 65 21 0D 4E 6F  t work, mate!.No
00402138  77 20 74 72 79 20 74 68 65 20 6E 65 78 74 20 43  w try the next C
00402148  72 61 63 6B 4D 65 21 00 1F 2C 37 36 3B 3D 28 19  rackMe!.,76;=(
00402158  3D 26 1A 31 2D 3B 37 3E 4E 6F 20 6C 75 63 6B 21  =&1-;7>No luck!
00402168  00 4E 6F 20 6C 75 63 6B 20 74 68 65 72 65 2C 20  .No luck there,
00402178  6D 61 74 65 21 00 31 32 33 34 35 36 37 38 39 00  mate!.123456789.
00402188  00 00 00 00 00 00 00 00 00 00 54 72 79 20 74 6F  ..........Try to
00402198  20 63 72 61 63 6B 20 6D 65 21 00 4D 65 73 73 69   crack me!.Messi
004021A8  6E 67 5F 69 6E 5F 62 79 74 65 73 00 00 00 00 00  ng_in_bytes.....

Estado del DUMP después del XOR.

00402118  0A 47 6F 6F 64 20 77 6F 72 6B 21 00 47 72 65 61  .Good work!.Grea
00402128  74 20 77 6F 72 6B 2C 20 6D 61 74 65 21 0D 4E 6F  t work, mate!.No
00402138  77 20 74 72 79 20 74 68 65 20 6E 65 78 74 20 43  w try the next C
00402148  72 61 63 6B 4D 65 21 00 1F 2C 37 36 3B 3D 28 19  rackMe!.,76;=(
00402158  3D 26 1A 31 2D 3B 37 3E 4E 6F 20 6C 75 63 6B 21  =&1-;7>No luck!
00402168  00 4E 6F 20 6C 75 63 6B 20 74 68 65 72 65 2C 20  .No luck there,
00402178  6D 61 74 65 21 00 7C 57 40 47 5C 58 50 67 50 5E  mate!.|W@G\XPgP^
00402188  00 00 00 00 00 00 00 00 00 00 54 72 79 20 74 6F  ..........Try to
00402198  20 63 72 61 63 6B 20 6D 65 21 00 4D 65 73 73 69   crack me!.Messi
004021A8  6E 67 5F 69 6E 5F 62 79 74 65 73                 ng_in_bytes

A continuación comprueba nuestro serial XOReado con los bytes en memoria.

004013B8     /$  33FF                     XOR EDI,EDI
004013BA     |.  33C9                     XOR ECX,ECX
004013BC     |.  8A0D 18214000            MOV CL,BYTE PTR DS:[402118]                                
004013C2     |.  8B7424 04                MOV ESI,DWORD PTR SS:[ESP+4]                    ; APUNTA AL DUMP 40217E
004013C6     |.  BF 50214000              MOV EDI,CRACKME2.00402150                       ; APUNTA AL DUMP 402150
004013CB     |.  F3:A6                    REPE CMPS BYTE PTR ES:[EDI],BYTE PTR DS:[ESI]   ; VER NOTA**
004013CD     \.  C3                       RETN

Nota**

Si buscamos el comando REPE encontramos que si el flag Z = 1 el bucle se corta y que trabaja con bytes. El problema es que en Olly la instrucción REPE nosotros la vemos con un solo paso y nos puede pasar desapercibida.
En resumen, está comprobando los bytes de las direcciones 402150 (1F 2C 37 36 3B 3D 28 19 3D 26 1A 31 2D 3B 37 3E) con nuestro serial XOReado, 40217E en adelante, por lo que si hacemos XOR entre los bytes de 402150 y la frase «Messing_in_bytes» obtendremos la clave correcta.

M  e  s  s  i  n  g  _  i  n  _  b  y  t  e  s
4D 65 73 73 69 6E 67 5F 69 6E 5F 62 79 74 65 73
                                                XOR
1F 2C 37 36 3B 3D 28 19 3D 26 1A 31 2D 3B 37 3E
-----------------------------------------------
52 49 44 45 52 53 4F 46 54 48 45 53 54 4F 52 4D
R  I  D  E  R  S  O  F  T  H  E  S  T  O  R  M

Serial: RIDERSOFTHESTORM

Links

Reversing - Nosotros y ChatGPT contra un ELF desde Windows
Intro Antes que nada, es importante saber que un archivo ELF en Linux es equivalente a un archivo EXE en
Migas de pan
Se nos entrega el siguiente ELF: Extracción de la Flag Si nos fijamos en las líneas 41 a la 45
Andy's Keygenme Keygen (AutoIt)
Introducción  Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro
Keygen para el Crackme#1 de DiS
Intro Hoy tenemos un crackme realizado en ensamblador y sin empacar. Consiste en el típico serial asociado a un nombre

por ·Sin comentarios

Table of Contents

Intro

Antes que nada, es importante saber que un archivo ELF en Linux es equivalente a un archivo EXE en Windows. Dicho esto, es bastante común encontrarnos con ejecutables ELF en diversos CTFs (Capture The Flag), y a menudo representan un desafío para aquellos no familiarizados con el uso cotidiano de Linux. Sin embargo, tengo una buena noticia si no eres aficionado de Linux: existen herramientas que permiten realizar un análisis preliminar para determinar si es necesario abordar el problema desde Linux o si podemos resolverlo directamente desde Windows. Estas herramientas facilitan una transición más cómoda para los usuarios de Windows, permitiéndoles interactuar eficazmente con archivos ELF.

ELF

Un archivo ELF (Executable and Linkable Format) es un formato común de archivo para archivos ejecutables, código objeto, bibliotecas compartidas y volcados de memoria en sistemas basados en Unix, como Linux. Es el estándar de formato de archivo para programas compilados y enlazados en este tipo de sistemas operativos.

La cabecera de un archivo ELF es una estructura de datos al comienzo del archivo que proporciona información esencial sobre el contenido y la forma de procesar el archivo. Esta cabecera es fundamental para que el sistema operativo y otros programas puedan interpretar correctamente el archivo ELF. Aquí están los componentes clave de la cabecera de un archivo ELF:

  1. Identificación (e_ident): Esta sección incluye la magia del archivo ELF, representada por los primeros cuatro bytes 0x7F 'E' 'L' 'F'. También incluye información como la clase del archivo (32 o 64 bits), la codificación de datos (endianness), y la versión del formato ELF.
  2. Tipo (e_type): Indica el tipo de archivo ELF, como EXEC (ejecutable), DYN (biblioteca compartida), REL (relocalizable), entre otros.
  3. Máquina (e_machine): Especifica la arquitectura de hardware para la cual se diseñó el archivo, por ejemplo, x86, ARM.
  4. Versión (e_version): La versión del formato ELF, generalmente establecida en 1.
  5. Punto de Entrada (e_entry): La dirección de memoria virtual donde comienza la ejecución del proceso.
  6. Desplazamiento del Program Header (e_phoff): Indica dónde comienza el encabezado del programa en el archivo.
  7. Desplazamiento del Section Header (e_shoff): Indica dónde comienza el encabezado de la sección en el archivo.
  8. Flags (e_flags): Banderas específicas del procesador.
  9. Tamaño de esta cabecera (e_ehsize): El tamaño de la cabecera ELF.
  10. Tamaño del Program Header (e_phentsize): El tamaño de una entrada del encabezado del programa.
  11. Número de entradas del Program Header (e_phnum): El número total de entradas en el encabezado del programa.
  12. Tamaño del Section Header (e_shentsize): El tamaño de una entrada del encabezado de la sección.
  13. Número de entradas del Section Header (e_shnum): El número total de entradas en el encabezado de la sección.
  14. Índice del Section Header Table (e_shstrndx): El índice del encabezado de la sección que contiene los nombres de las secciones.

El reto

Se nos proporciona un fichero de 20KB que rápidamente catalogamos como ELF.

Para realizar un análisis preliminar siempre uso DogBolt, que no es más que un decompilador online con la ventaja de que usa varios motores y de esta forma casi siempre te da una decompilación aceptable. La versión actual tiene disponibles 11 motores y además es open source, ¿Qué más se puede pedir?

Echamos un vistazo y enseguida encontramos algo interesante.

La flag parece codificada de modo que vamos a indagar acerca de la función FUN_0010285d

Dentro de la función FUN_0010285d vemos que nuestra flag codificada la procesa la función FUN_00102752

Aquí os diría que depende de vuestra experiencia en programación veríais que se está procesando byte a byte la cadena de entrada (param_1) y haciendo a cada byte un XOR (^) con el param_3 (que es 1 según vemos en la llamada de la función FUN_00102752), pero en estos tiempos que corren vamos a preguntar a ChatGPT que opina.

ChatGPT

Le pido a ChapGPT que me analice el código y me responde:

Este código en C define una función llamada FUN_00102752 que realiza una operación de XOR (exclusivo OR) byte a byte sobre un bloque de memoria. La función toma tres parámetros:

  1. long param_1: Este parámetro es tratado como una dirección de memoria. Se utiliza como la base de un bloque de memoria sobre el que se realizará la operación.
  2. ulong param_2: Este parámetro especifica el tamaño del bloque de memoria que será afectado por la operación.
  3. byte param_3: Este es el valor de un solo byte que se utilizará en la operación XOR.

El cuerpo de la función consiste en un bucle for que itera sobre el bloque de memoria:

  • int local_c se declara como una variable local y se inicializa en 0. Esta variable actúa como un contador para el bucle.
  • La condición del bucle (ulong)(long)local_c < param_2 asegura que el bucle se ejecute sobre el rango completo del bloque de memoria especificado por param_2.
  • Dentro del bucle, *(byte *)(param_1 + local_c) = *(byte *)(param_1 + local_c) ^ param_3; realiza la operación XOR. Aquí, *(byte *)(param_1 + local_c) accede al byte actual en el bloque de memoria. Este byte se modifica aplicándole un XOR con param_3. La operación XOR se realiza entre el byte actual en la memoria y el valor de param_3, y el resultado se escribe de nuevo en la misma ubicación de memoria.

En resumen, la función FUN_00102752 modifica un bloque de memoria aplicando una operación XOR con un valor dado (param_3) a cada byte dentro del rango de memoria especificado desde param_1 hasta param_1 + param_2. Este tipo de operación es común en tareas como la manipulación de datos para cifrado/descifrado o para la generación de patrones específicos en un bloque de datos.

by ChatGPT

Ahora imaginad que no sois muy dados a programar o simplemente estáis vagos de modo que volvemos a recurrir a ChatGPT con el promt «Haz un XOR 1 con javascript a la cadena: gmfzuihr^vr^o^drx^nod^shfiu|» a lo que responde:

function xorString(str) {
return Array.from(str).map(char => String.fromCharCode(char.charCodeAt(0) ^ 1)).join(»);
}

console.log(xorString(‘gmfzuihr^vr^o^drx^nod^shfiu|’));

by ChatGPT

Copiamos el código y lo pegamos en un entorno online como por ejemplo playcode.io.

Este es un ejemplo simple, pero ¿percibís su potencial?

La imagen de portada de esta entrada ha sido generada con ChatGPT.

por ·Sin comentarios

Se nos entrega el siguiente ELF:

/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
   Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>

   Detected compiler: GNU C++
*/

#include <defs.h>


//-------------------------------------------------------------------------
// Function declarations

__int64 (**init_proc())(void);
void sub_1020();
// int printf(const char *format, ...);
// int getchar(void);
// int fflush(FILE *stream);
// __int64 __isoc99_scanf(const char *, ...); weak
// void __noreturn exit(int status);
// int __fastcall _cxa_finalize(void *);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
FILE **deregister_tm_clones();
__int64 register_tm_clones(); // weak
FILE **_do_global_dtors_aux();
__int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD); // weak
int __fastcall main(int argc, const char **argv, const char **envp);
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3);
void _libc_csu_fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// int __fastcall __cxa_finalize(void *);
// __int64 _gmon_start__(void); weak

//-------------------------------------------------------------------------
// Data declarations

_UNKNOWN _libc_csu_init;
__int64 (__fastcall *_frame_dummy_init_array_entry)() = &frame_dummy; // weak
__int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)() = &_do_global_dtors_aux; // weak
void *_dso_handle = &_dso_handle; // idb
char *a = "MdfnJk"; // weak
char *b = "jYx}"; // weak
char *c = "gWmfk"; // weak
char *d = "mlvpc"; // weak
char *f = "neU++w"; // weak
FILE *_bss_start; // idb
char completed_0; // weak


//----- (0000000000001000) ----------------------------------------------------
__int64 (**init_proc())(void)
{
  __int64 (**result)(void); // rax

  result = &_gmon_start__;
  if ( &_gmon_start__ )
    return (__int64 (**)(void))_gmon_start__();
  return result;
}
// 40D0: using guessed type __int64 _gmon_start__(void);

//----- (0000000000001020) ----------------------------------------------------
void sub_1020()
{
  JUMPOUT(0LL);
}
// 1026: control flows out of bounds to 0

//----- (0000000000001090) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
  __int64 v3; // rax
  int v4; // esi
  __int64 v5; // [rsp-8h] [rbp-8h] BYREF
  char *retaddr; // [rsp+0h] [rbp+0h] BYREF

  v4 = v5;
  v5 = v3;
  _libc_start_main(
    (int (__fastcall *)(int, char **, char **))main,
    v4,
    &retaddr,
    (void (*)(void))_libc_csu_init,
    _libc_csu_fini,
    a3,
    &v5);
  __halt();
}
// 1096: positive sp value 8 has been found
// 109D: variable 'v3' is possibly undefined

//----- (00000000000010C0) ----------------------------------------------------
FILE **deregister_tm_clones()
{
  return &_bss_start;
}

//----- (00000000000010F0) ----------------------------------------------------
__int64 register_tm_clones()
{
  return 0LL;
}
// 10F0: using guessed type __int64 register_tm_clones();

//----- (0000000000001130) ----------------------------------------------------
FILE **_do_global_dtors_aux()
{
  FILE **result; // rax

  if ( !completed_0 )
  {
    if ( &__cxa_finalize )
      _cxa_finalize(_dso_handle);
    result = deregister_tm_clones();
    completed_0 = 1;
  }
  return result;
}
// 4080: using guessed type char completed_0;

//----- (0000000000001175) ----------------------------------------------------
int __fastcall main(int argc, const char **argv, const char **envp)
{
  char v4; // [rsp+7h] [rbp-9h] BYREF
  int v5; // [rsp+8h] [rbp-8h]
  bool v6; // [rsp+Fh] [rbp-1h]

  v6 = 1;
  v5 = 0;
  while ( v6 )
  {
    fflush(_bss_start);
    printf("\nIntroduce la letra correcta:\t");
    __isoc99_scanf("%c", &v4);
    getchar();
    if ( v5 > 5 )
    {
      if ( v5 > 9 )
      {
        if ( v5 > 14 )
        {
          if ( v5 > 19 )
            v6 = comprobacion(v4, f[v5 - 20], 10);
          else
            v6 = comprobacion(v4, d[v5 - 15], 2);
        }
        else
        {
          v6 = comprobacion(v4, c[v5 - 10], 8);
        }
      }
      else
      {
        v6 = comprobacion(v4, b[v5 - 6], 17);
      }
    }
    else
    {
      v6 = comprobacion(v4, a[v5], 5);
    }
    if ( !v6 )
    {
      printf("Incorrecta");
      exit(1);
    }
    printf("\n%c\n", (unsigned int)v4);
    if ( v5 == 25 )
    {
      printf("Ya tienes la flag!!");
      exit(1);
    }
    ++v5;
  }
  return 0;
}
// 1060: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 4050: using guessed type char *a;
// 4058: using guessed type char *b;
// 4060: using guessed type char *c;
// 4068: using guessed type char *d;
// 4070: using guessed type char *f;

//----- (0000000000001352) ----------------------------------------------------
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3)
{
  return a1 == (a3 ^ a2);
}

//----- (0000000000001390) ----------------------------------------------------
void __fastcall _libc_csu_init(unsigned int a1, __int64 a2, __int64 a3)
{
  signed __int64 v4; // rbp
  __int64 i; // rbx

  init_proc();
  v4 = &_do_global_dtors_aux_fini_array_entry - &_frame_dummy_init_array_entry;
  if ( v4 )
  {
    for ( i = 0LL; i != v4; ++i )
      ((void (__fastcall *)(_QWORD, __int64, __int64))*(&_frame_dummy_init_array_entry + i))(a1, a2, a3);
  }
}
// 1170: using guessed type __int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD);
// 3DE8: using guessed type __int64 (__fastcall *_frame_dummy_init_array_entry)();
// 3DF0: using guessed type __int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)();

//----- (00000000000013F4) ----------------------------------------------------
void term_proc()
{
  ;
}

Extracción de la Flag

Si nos fijamos en las líneas 41 a la 45 vemos las siguientes cadenas:

a = «MdfnJk»
b = «jYx}»
c = «gWmfk»
d = «mlvpc»
f = «neU++w»

Usaremos las cadenas y los valores XOR especificados para cada rango de v5 en el main (líneas 123 a 182) para determinar los caracteres correctos.

Para v5 de 0 a 5: v6 = comprobacion(v4, a[v5], 5);
Significa que: v4 debe ser igual a a[v5] ^ 5

Para v5 de 6 a 9: v6 = comprobacion(v4, b[v5 – 6], 17);
Significa que: v4 debe ser igual a b[v5 – 6] ^ 17

Para v5 de 10 a 14: v6 = comprobacion(v4, c[v5 – 10], 8);
Significa que: v4 debe ser igual a c[v5 – 10] ^ 8

Para v5 de 15 a 19: v6 = comprobacion(v4, d[v5 – 15], 2);
Significa que: v4 debe ser igual a d[v5 – 15] ^ 2

Para v5 de 20 a 25: v6 = comprobacion(v4, f[v5 – 20], 10);
Significa que: v4 debe ser igual a f[v5 – 20] ^ 10

Cálculo de los caracteres correctos:
Para v5 de 0 a 5:
a[0] = ‘M’, M ^ 5 = 0x4D ^ 0x05 = 0x48 -> ‘H’
a[1] = ‘d’, d ^ 5 = 0x64 ^ 0x05 = 0x61 -> ‘a’
a[2] = ‘f’, f ^ 5 = 0x66 ^ 0x05 = 0x63 -> ‘c’
a[3] = ‘n’, n ^ 5 = 0x6E ^ 0x05 = 0x6B -> ‘k’
a[4] = ‘J’, J ^ 5 = 0x4A ^ 0x05 = 0x4F -> ‘O’
a[5] = ‘k’, k ^ 5 = 0x6B ^ 0x05 = 0x6E -> ‘n’
Resulta en la cadena: HackOn

Para v5 de 6 a 9:
b[0] = ‘j’, j ^ 17 = 0x6A ^ 0x11 = 0x7B -> ‘{‘
b[1] = ‘Y’, Y ^ 17 = 0x59 ^ 0x11 = 0x48 -> ‘H’
b[2] = ‘x’, x ^ 17 = 0x78 ^ 0x11 = 0x69 -> ‘i’
b[3] = ‘}’, } ^ 17 = 0x7D ^ 0x11 = 0x6C -> ‘l’
Resulta en la cadena: {Hil

Para v5 de 10 a 14:
c[0] = ‘g’, g ^ 8 = 0x67 ^ 0x08 = 0x6F -> ‘o’
c[1] = ‘W’, W ^ 8 = 0x57 ^ 0x08 = 0x5F -> ‘_’
c[2] = ‘m’, m ^ 8 = 0x6D ^ 0x08 = 0x65 -> ‘e’
c[3] = ‘f’, f ^ 8 = 0x66 ^ 0x08 = 0x6E -> ‘n’
c[4] = ‘k’, k ^ 8 = 0x6B ^ 0x08 = 0x63 -> ‘c’
Resulta en la cadena: o_enc

Para v5 de 15 a 19:
d[0] = ‘m’, m ^ 2 = 0x6D ^ 0x02 = 0x6F -> ‘o’
d[1] = ‘l’, l ^ 2 = 0x6C ^ 0x02 = 0x6E -> ‘n’
d[2] = ‘v’, v ^ 2 = 0x76 ^ 0x02 = 0x74 -> ‘t’
d[3] = ‘p’, p ^ 2 = 0x70 ^ 0x02 = 0x72 -> ‘r’
d[4] = ‘c’, c ^ 2 = 0x63 ^ 0x02 = 0x61 -> ‘a’
Resulta en la cadena: ontra

Para v5 de 20 a 25:
f[0] = ‘n’, n ^ 10 = 0x6E ^ 0x0A = 0x64 -> ‘d’
f[1] = ‘e’, e ^ 10 = 0x65 ^ 0x0A = 0x6F -> ‘o’
f[2] = ‘U’, U ^ 10 = 0x55 ^ 0x0A = 0x5F -> ‘_‘
f[3] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[4] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[5] = ‘w’, w ^ 10 = 0x77 ^ 0x0A = 0x7D -> ‘}’
Resulta en la cadena: do_!!}

Uniendo todas las partes, obtenemos la flag completa: HackOn{Hilo_enc_ontrado_!!}

por ·Sin comentarios

Introducción

 Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro keygen. Como comprobareis si no se ofusca o se toman otro tipo de medidas recuperar información sensible es muy sencillo.

AutoIt es un lenguaje freeware multiproposito y de automatización para Microsoft Windows. Es un Visual Basic Killer, ya que mejora las características de los ejecutables (entre otras portabilidad, velocidad y peso, no fat-coding), y facilitan la programación con un buen repertorio de funciones «pre-diseñadas», y usando un Basic de fácil aprendizaje. Se ha expandido desde sus comienzos de automatización incluyendo muchas mejoras en el diseño del lenguaje de programación y sobre todo en nuevas funcionalidades.

El Script

Func CHECKKEY($USER, $PASS)
Local $OPKEY = "", $SIG = ""
Local $USER_LEN = StringLen($USER)
Local $PASS_LEN = StringLen($PASS)
If $USER_LEN < $PASS_LEN Then
MsgBox(0, "ERROR", "Invalid username or key.")
Exit
ElseIf $USER_LEN < 4 Then
MsgBox(0, "ERROR", "Invalid username or key.")
Exit
EndIf
$PASS_INT = Int($USER_LEN / $PASS_LEN)
$PASS_MOD = Mod($USER_LEN, $PASS_LEN)
$OPKEY = _STRINGREPEAT($PASS, $PASS_INT) & StringLeft($PASS, $PASS_MOD)
For $INDEX = 1 To $USER_LEN
$SIG &= Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), Asc(StringMid($OPKEY, $USER_LEN - $INDEX + 1, 1))))
Next
If $SIG = _STRINGREPEAT(Chr(32), $USER_LEN) Then
MsgBox(0, "INFO", "Your key was registered.")
Exit
Else
MsgBox(0, "INFO", "Your key is invalid.")
EndIf
EndFunc

 El Algoritmo

El algoritmo es tremendamente sencillo ya que es nuestro nombre al revés y en mayúsculas.

 Modificando el script para generar nuestro propio keygen

El decompilador se llama myAut2exe y tiene este aspecto.

01-09-2014 11-56-37

Programar en AutoIt es muy sencillo e intuitivo. Nuestro keygen quedaría así.

$MAIN = GUICreate("Another keygen by deurus", 300, 80, -1, -1, 382205952, 385)
$NAME_LBL = GUICtrlCreateLabel("Username", 5, 5, 60, 20, BitOR(4096, 1))
$NAME_INP = GUICtrlCreateInput("", 70, 5, 225, 20, 1)
$PASS_LBL = GUICtrlCreateLabel("Key", 5, 30, 60, 20, BitOR(4096, 1))
$PASS_INP = GUICtrlCreateInput("", 70, 30, 225, 20, 1)
$REGISTER = GUICtrlCreateButton("Register", 5, 55, 60, 20)
$GIVE_UP = GUICtrlCreateButton("Generate", 70, 55, 60, 20)    <- Change name of button, Give Up by Generate
$TASK = GUICtrlCreateButton("?", 140, 55, 20, 20)
$AUTHOR = GUICtrlCreateLabel("keygen by deurus", 165, 55, 130, 20, BitOR(4096, 1))
GUISetState(@SW_SHOW, $MAIN)
While True
    $MSG = GUIGetMsg()
    Switch $MSG
        Case $REGISTER
            Call("CHECKKEY", GUICtrlRead($NAME_INP), GUICtrlRead($PASS_INP))
        Case $GIVE_UP
            Call("GETKEY", GUICtrlRead($NAME_INP), GUICtrlRead($PASS_INP))    <- Add the function to the button
        Case $TASK
            MsgBox(0, "Info", "keygen by deurus")
        Case - 3
            Exit
    EndSwitch
    Sleep(15)
WEnd

Func GETKEY($USER, $PASS)        <- this is our keygen function
    Local $OPKEY = "", $SIG = ""
    Local $USER_LEN = StringLen($USER)
    Local $PASS_LEN = StringLen($USER)
    If $USER_LEN < 4 Then
        GUICtrlSetData($PASS_INP  ,"min 4 chars");
    Else
    For $INDEX = 1 To $USER_LEN
        $SIG = Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), 32)) & $SIG
    Next
        GUICtrlSetData($PASS_INP  ,$SIG);
    EndIf
EndFunc

Func CHECKKEY($USER, $PASS)        <- check function, the original
    Local $OPKEY = "", $SIG = ""
    Local $USER_LEN = StringLen($USER)
    Local $PASS_LEN = StringLen($PASS)
    If $USER_LEN < $PASS_LEN Then
        MsgBox(0, "ERROR", "Invalid username or key.")
    ElseIf $USER_LEN < 4 Then
        MsgBox(0, "ERROR", "Invalid username or key.")
        Exit
    EndIf
    $PASS_INT = Int($USER_LEN / $PASS_LEN)
    $PASS_MOD = Mod($USER_LEN, $PASS_LEN)
    $OPKEY = _STRINGREPEAT($PASS, $PASS_INT) & StringLeft($PASS, $PASS_MOD)
    For $INDEX = 1 To $USER_LEN
        $SIG &= Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), Asc(StringMid($OPKEY, $USER_LEN - $INDEX + 1, 1))))
    Next
    If $SIG = _STRINGREPEAT(Chr(32), $USER_LEN) Then
        MsgBox(0, "INFO", "Your key was registered.")
    Else
        MsgBox(0, "INFO", "Your key is invalid.")
    EndIf
EndFunc

Este es el resultado.

01-09-2014 12-18-28

Links

Migas de pan
Se nos entrega el siguiente ELF: Extracción de la Flag Si nos fijamos en las líneas 41 a la 45
Blooper Tech Movie II – Hackers
En esta ocasión vamos a hablar de una película de culto de los años 90, Hackers - Piratas Informáticos. La
Solución al Time Trial de Detten
Intro Hoy tenemos aquí otro crackme sacado del baúl de los recuerdos. En este caso se trata de una protección
Keygen para el Crackme Sweeet Dream 1.0 de 2Sweeet
Intro Hoy tenemos aquí un crackme del año 2000 empacado y con un algoritmo aunque no muy complicado largo de

por ·Sin comentarios

Se nos entrega el siguiente ELF:

/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
   Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>

   Detected compiler: GNU C++
*/

#include <defs.h>


//-------------------------------------------------------------------------
// Function declarations

__int64 (**init_proc())(void);
void sub_1020();
// int printf(const char *format, ...);
// int getchar(void);
// int fflush(FILE *stream);
// __int64 __isoc99_scanf(const char *, ...); weak
// void __noreturn exit(int status);
// int __fastcall _cxa_finalize(void *);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
FILE **deregister_tm_clones();
__int64 register_tm_clones(); // weak
FILE **_do_global_dtors_aux();
__int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD); // weak
int __fastcall main(int argc, const char **argv, const char **envp);
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3);
void _libc_csu_fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// int __fastcall __cxa_finalize(void *);
// __int64 _gmon_start__(void); weak

//-------------------------------------------------------------------------
// Data declarations

_UNKNOWN _libc_csu_init;
__int64 (__fastcall *_frame_dummy_init_array_entry)() = &frame_dummy; // weak
__int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)() = &_do_global_dtors_aux; // weak
void *_dso_handle = &_dso_handle; // idb
char *a = "MdfnJk"; // weak
char *b = "jYx}"; // weak
char *c = "gWmfk"; // weak
char *d = "mlvpc"; // weak
char *f = "neU++w"; // weak
FILE *_bss_start; // idb
char completed_0; // weak


//----- (0000000000001000) ----------------------------------------------------
__int64 (**init_proc())(void)
{
  __int64 (**result)(void); // rax

  result = &_gmon_start__;
  if ( &_gmon_start__ )
    return (__int64 (**)(void))_gmon_start__();
  return result;
}
// 40D0: using guessed type __int64 _gmon_start__(void);

//----- (0000000000001020) ----------------------------------------------------
void sub_1020()
{
  JUMPOUT(0LL);
}
// 1026: control flows out of bounds to 0

//----- (0000000000001090) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
  __int64 v3; // rax
  int v4; // esi
  __int64 v5; // [rsp-8h] [rbp-8h] BYREF
  char *retaddr; // [rsp+0h] [rbp+0h] BYREF

  v4 = v5;
  v5 = v3;
  _libc_start_main(
    (int (__fastcall *)(int, char **, char **))main,
    v4,
    &retaddr,
    (void (*)(void))_libc_csu_init,
    _libc_csu_fini,
    a3,
    &v5);
  __halt();
}
// 1096: positive sp value 8 has been found
// 109D: variable 'v3' is possibly undefined

//----- (00000000000010C0) ----------------------------------------------------
FILE **deregister_tm_clones()
{
  return &_bss_start;
}

//----- (00000000000010F0) ----------------------------------------------------
__int64 register_tm_clones()
{
  return 0LL;
}
// 10F0: using guessed type __int64 register_tm_clones();

//----- (0000000000001130) ----------------------------------------------------
FILE **_do_global_dtors_aux()
{
  FILE **result; // rax

  if ( !completed_0 )
  {
    if ( &__cxa_finalize )
      _cxa_finalize(_dso_handle);
    result = deregister_tm_clones();
    completed_0 = 1;
  }
  return result;
}
// 4080: using guessed type char completed_0;

//----- (0000000000001175) ----------------------------------------------------
int __fastcall main(int argc, const char **argv, const char **envp)
{
  char v4; // [rsp+7h] [rbp-9h] BYREF
  int v5; // [rsp+8h] [rbp-8h]
  bool v6; // [rsp+Fh] [rbp-1h]

  v6 = 1;
  v5 = 0;
  while ( v6 )
  {
    fflush(_bss_start);
    printf("\nIntroduce la letra correcta:\t");
    __isoc99_scanf("%c", &v4);
    getchar();
    if ( v5 > 5 )
    {
      if ( v5 > 9 )
      {
        if ( v5 > 14 )
        {
          if ( v5 > 19 )
            v6 = comprobacion(v4, f[v5 - 20], 10);
          else
            v6 = comprobacion(v4, d[v5 - 15], 2);
        }
        else
        {
          v6 = comprobacion(v4, c[v5 - 10], 8);
        }
      }
      else
      {
        v6 = comprobacion(v4, b[v5 - 6], 17);
      }
    }
    else
    {
      v6 = comprobacion(v4, a[v5], 5);
    }
    if ( !v6 )
    {
      printf("Incorrecta");
      exit(1);
    }
    printf("\n%c\n", (unsigned int)v4);
    if ( v5 == 25 )
    {
      printf("Ya tienes la flag!!");
      exit(1);
    }
    ++v5;
  }
  return 0;
}
// 1060: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 4050: using guessed type char *a;
// 4058: using guessed type char *b;
// 4060: using guessed type char *c;
// 4068: using guessed type char *d;
// 4070: using guessed type char *f;

//----- (0000000000001352) ----------------------------------------------------
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3)
{
  return a1 == (a3 ^ a2);
}

//----- (0000000000001390) ----------------------------------------------------
void __fastcall _libc_csu_init(unsigned int a1, __int64 a2, __int64 a3)
{
  signed __int64 v4; // rbp
  __int64 i; // rbx

  init_proc();
  v4 = &_do_global_dtors_aux_fini_array_entry - &_frame_dummy_init_array_entry;
  if ( v4 )
  {
    for ( i = 0LL; i != v4; ++i )
      ((void (__fastcall *)(_QWORD, __int64, __int64))*(&_frame_dummy_init_array_entry + i))(a1, a2, a3);
  }
}
// 1170: using guessed type __int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD);
// 3DE8: using guessed type __int64 (__fastcall *_frame_dummy_init_array_entry)();
// 3DF0: using guessed type __int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)();

//----- (00000000000013F4) ----------------------------------------------------
void term_proc()
{
  ;
}

Extracción de la Flag

Si nos fijamos en las líneas 41 a la 45 vemos las siguientes cadenas:

a = «MdfnJk»
b = «jYx}»
c = «gWmfk»
d = «mlvpc»
f = «neU++w»

Usaremos las cadenas y los valores XOR especificados para cada rango de v5 en el main (líneas 123 a 182) para determinar los caracteres correctos.

Para v5 de 0 a 5: v6 = comprobacion(v4, a[v5], 5);
Significa que: v4 debe ser igual a a[v5] ^ 5

Para v5 de 6 a 9: v6 = comprobacion(v4, b[v5 – 6], 17);
Significa que: v4 debe ser igual a b[v5 – 6] ^ 17

Para v5 de 10 a 14: v6 = comprobacion(v4, c[v5 – 10], 8);
Significa que: v4 debe ser igual a c[v5 – 10] ^ 8

Para v5 de 15 a 19: v6 = comprobacion(v4, d[v5 – 15], 2);
Significa que: v4 debe ser igual a d[v5 – 15] ^ 2

Para v5 de 20 a 25: v6 = comprobacion(v4, f[v5 – 20], 10);
Significa que: v4 debe ser igual a f[v5 – 20] ^ 10

Cálculo de los caracteres correctos:
Para v5 de 0 a 5:
a[0] = ‘M’, M ^ 5 = 0x4D ^ 0x05 = 0x48 -> ‘H’
a[1] = ‘d’, d ^ 5 = 0x64 ^ 0x05 = 0x61 -> ‘a’
a[2] = ‘f’, f ^ 5 = 0x66 ^ 0x05 = 0x63 -> ‘c’
a[3] = ‘n’, n ^ 5 = 0x6E ^ 0x05 = 0x6B -> ‘k’
a[4] = ‘J’, J ^ 5 = 0x4A ^ 0x05 = 0x4F -> ‘O’
a[5] = ‘k’, k ^ 5 = 0x6B ^ 0x05 = 0x6E -> ‘n’
Resulta en la cadena: HackOn

Para v5 de 6 a 9:
b[0] = ‘j’, j ^ 17 = 0x6A ^ 0x11 = 0x7B -> ‘{‘
b[1] = ‘Y’, Y ^ 17 = 0x59 ^ 0x11 = 0x48 -> ‘H’
b[2] = ‘x’, x ^ 17 = 0x78 ^ 0x11 = 0x69 -> ‘i’
b[3] = ‘}’, } ^ 17 = 0x7D ^ 0x11 = 0x6C -> ‘l’
Resulta en la cadena: {Hil

Para v5 de 10 a 14:
c[0] = ‘g’, g ^ 8 = 0x67 ^ 0x08 = 0x6F -> ‘o’
c[1] = ‘W’, W ^ 8 = 0x57 ^ 0x08 = 0x5F -> ‘_’
c[2] = ‘m’, m ^ 8 = 0x6D ^ 0x08 = 0x65 -> ‘e’
c[3] = ‘f’, f ^ 8 = 0x66 ^ 0x08 = 0x6E -> ‘n’
c[4] = ‘k’, k ^ 8 = 0x6B ^ 0x08 = 0x63 -> ‘c’
Resulta en la cadena: o_enc

Para v5 de 15 a 19:
d[0] = ‘m’, m ^ 2 = 0x6D ^ 0x02 = 0x6F -> ‘o’
d[1] = ‘l’, l ^ 2 = 0x6C ^ 0x02 = 0x6E -> ‘n’
d[2] = ‘v’, v ^ 2 = 0x76 ^ 0x02 = 0x74 -> ‘t’
d[3] = ‘p’, p ^ 2 = 0x70 ^ 0x02 = 0x72 -> ‘r’
d[4] = ‘c’, c ^ 2 = 0x63 ^ 0x02 = 0x61 -> ‘a’
Resulta en la cadena: ontra

Para v5 de 20 a 25:
f[0] = ‘n’, n ^ 10 = 0x6E ^ 0x0A = 0x64 -> ‘d’
f[1] = ‘e’, e ^ 10 = 0x65 ^ 0x0A = 0x6F -> ‘o’
f[2] = ‘U’, U ^ 10 = 0x55 ^ 0x0A = 0x5F -> ‘_‘
f[3] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[4] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[5] = ‘w’, w ^ 10 = 0x77 ^ 0x0A = 0x7D -> ‘}’
Resulta en la cadena: do_!!}

Uniendo todas las partes, obtenemos la flag completa: HackOn{Hilo_enc_ontrado_!!}

por ·Sin comentarios

En esta ocasión vamos a hablar de una película de culto de los años 90, Hackers – Piratas Informáticos. La verdad es que aunque puede ser entretenida, tecnológicamente es una pesadilla y es que esta película es un claro ejemplo de cuando Hollywood prefiere agradar visualmente a representar escenas realistas.

Tras cuatro minutos en los que se nos presenta a Dade (Jonny Lee Miller) y sus problemas con la ley a una temprana edad, saltamos unos años después hasta ver a Dade encerrado en su habitación volviendo a las andadas intentando acceder ilegítimamente a los servidores de una cadena de televisión. Para ello hace uso de algo muy conocido en el mundillo Hacker, la Ingeniería Social, y es que aunque ahora disponemos de «cierta» conciencia en seguridad informática, en los años 90 no había ninguna. Bien, el caso es que Dade llama a las oficinas de la citada cadena de televisión a una hora en la que no hay más que el vigilante de seguridad y éste le proporciona un número que debemos suponer que es la IP de un Módem y comienza la intrusión.

BTM

Para empezar, se le ve al protagonista escribir comandos cuando en la pantalla no hay más que una animación en algo parecido a una ventana de terminal al estilo «Commander», pero no vemos lo que escribe, algo irreal.

vlcsnap-2015-11-25-18h00m25s936

A continuación y como por arte de magia entra en el sistema y lo que se muestra es una animación parpadeante con el logo de la compañia y el nombre del sistema al que estamos accediendo, también irreal.

vlcsnap-2015-11-25-12h43m18s762

Finalmente nos muestra sus intenciones, y son nada más y nada menos que cambiar la programación actual simplemente cambiando de VHS, inmejorable. A continuación os muestro la secuencia.

Por lo menos nos queda el consuelo de que cambia la tertulia de un tipejo con ciertos prejuicios raciales por una programación más interesante como «The Outer limits«, aquí conocida como «Más allá del límite«.

El resto de escenas informáticas de la película carecen de veracidad, la única que se salva, puede ser cuando accede al servidor del Instituto para programar el sistema contra incendios y vengarse de Kate (Angelina Jolie), ya que las imágenes que aparecen son de los primeros entornos gráficos de Mac.

vlcsnap-2015-11-25-18h29m08s043

vlcsnap-2015-11-25-18h29m15s390

vlcsnap-2015-11-25-18h29m31s550

Es extraño que casi todas las intrusiones las realiza desde su propia casa, algo poco inteligente, ya que por muy bueno que seas, siempre dejas huellas. Solo cuando se enfrentan a un Super-Hacker se empiezan a tomar las cosas en serio y realizan los ataques desde cabinas telefónicas.

En la película También hacen mención al Phreaking y a algunos de los libros que eran famosos por aquella época pero poco más que destacar. Por todo esto y mucho más, y aunque me caen igual de bien tanto Angelina como Jonny, la película se merece un majestuoso sello de BTM.

hackers_sello

Enlaces

Solución al KeyGenMe1 (RSA127) de C00lw0lf
Introducción Funcionamiento de RSA OllyDbg Calculando la clave privada (d) Ejemplo operacional Keygen Links Introducción Segunda crackme con RSA que
Cruehead's Crackme 3.0 Keygen [3/3]
Introducción Esta es la tercera y última entrega de los crackmes de Cruehead. En esta ocasión nos enfrentamos a un
Keygen para el KeygenMe#01 de eBuC - Comparación lineal
Primeras impresiones Analizamos el programa con PEiD y nos muestra que está hecho en ensamblador. Unas pruebas introduciendo datos nos
lost_in_bin
Estamos ante un ELF un poco más interesante que los vistos anteriormente. Básicamente porque es divertido y fácil encontrar la

por ·Sin comentarios
Aviso: Este crackme forma parte de una serie de pruebas de Yoire.com que todavía está en activo. Lo ético si continuas leyendo este manual es que no utilices la respuesta para completar la prueba sin esfuerzo. 😉

Analizando…

Cargamos el crackme en Ollydbg y vamos a las «Referenced Strings«. Vemos una referencia muy interesante que se llama «checkkey«.

 Pinchamos sobre ella y aparecemos aquí:

Vemos una referencia a «GetDlgItemTextA» y depués un Call también interesante, vamos a explorarlo.

Entendiendo la rutina de comprobación del serial

 

Dentro del Call hay dos bucles, uno realiza una operación con nuestro serial (bucle nombre) y el otro comprueba nuestro serial con «3d34273130276a» dígito a dígito (bucle comprobación).

Bucle nombre se puede resumir así:

MOVSX EAX,BYTE PTR DS:[EBX]   --> Dígito a EAX
XOR EAX,55                    --> EAX xor 55
...
CMP BYTE PTR DS:[EBX],0       --> ¿hemos acabado?
JNZ SHORT 10001022            --> bucle
LEA ECX,DWORD PTR SS:[EBP-20] --> ECX = nuestro serial xoreado

Bucle comprobación se podría resumir así:

MOV EDX,10006000             --> EDX = "3d34273130276a"
...
MOV AL,BYTE PTR DS:[ECX]     --> AL = 1ºdígito serial xoreado
CMP AL,BYTE PTR DS:[ECX+EDX] --> AL = 1ºdígito de EDX?
JNZ SHORT 1000105A           --> Si no son iguales bad boy
INC ECX 

TEST AL,AL
JNZ SHORT 1000104A           --> bucle

Ejemplo para «deurus».

   Nombre: d  e  u  r  u  s
Ascii hex: 64 65 75 72 75 73 
   XOR 55: 31 30 20 27 20 26

Serial XOReado para deurus sería = 313020272026 que obviamente se aleja bastante de 3d34273130276a.
Por suerte XOR es una función reversible por lo que si revertimos 3d34273130276a nos dará el serial correcto.

Serial correcto XOReado: 3d 34 27 31 30 27 6a
XOR 55:                  68 61 72 64 65 72 3F
Valor ascii:             h  a  r  d  e  r  ?

Links

Stego - Bytes en bruto
Toda esta aventura comienza con un archivo llamado pretty_raw, sin extensión. Porque sí. Porque las extensiones son una invención heredada
Reversing - Nosotros y ChatGPT contra un ELF desde Windows
Intro Antes que nada, es importante saber que un archivo ELF en Linux es equivalente a un archivo EXE en
CanYouHack.it Mobile2 Challenge - Follow The Web (English)
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en
Digi Logic Challenge
AVISO: Debido a que este reto está en activo no publicaré a donde pertenece. El reto en cuestión nos presenta

por ·Sin comentarios

Toda esta aventura comienza con un archivo llamado pretty_raw, sin extensión. Porque sí. Porque las extensiones son una invención heredada de CP/M, precursor de MS-DOS, que Windows terminó de popularizar. Porque son innecesarias. Y porque echo de menos cuando los archivos se reconocían por sus permisos… y no por cómo se llamaban.

Como iba diciendo, todo esto comienza mediante el análisis de pretty_raw. Mirando debajo de la falda con un editor hexadecimal encontramos unos cuantos bytes aleatorios hasta dar con una cabecera PNG.

Si atendemos a la captura, justo antes de la cabecera PNG tenemos 116.254 bytes (0x1C61E). Tomad nota que este número será relevante más adelante.

Extraemos el PNG, lo visualizamos y lo pasamos por todas las herramientas habidas y por haber. Nada funciona. Volvemos a visualizarlo con atención y vemos que hace referencia a un archivo llamado flag.png con unas dimensiones que no coinciden con la extraída.

Toca centrarse y pensar en que camino tomar. Hemos gastado tiempo con el PNG extraído y quizá lo mejor sea centrarse en los bytes que inicialmente hemos descartado. En concreto se trata de un bloque de 116.254 bytes, pero espera, 1570×74=116.180 bytes. ¡Mierda!, no coincide exactamente con los bytes extraídos. Bueno, da igual. Si suponemos que el PNG que buscamos no tiene compresión y que cada pixel ocupa un byte (escala de grises y 8 bits), su tamaño depende únicamente de la geometría y de cómo se almacenan las filas en memoria. Vamos a procesarlo con Python para salir de dudas.

import numpy as np
from PIL import Image

INPUT_FILE  = "pretty_raw"
OUTPUT_FILE = "pretty_raw_flag.png"

WIDTH  = 1570 # ¿estás seguro?
HEIGHT = 74
DEPTH  = 8  # bits

# Leer archivo como RAW
with open(INPUT_FILE, "rb") as f:
    raw = f.read()

expected_size = WIDTH * HEIGHT
if len(raw) < expected_size:
    raise ValueError("El archivo no tiene suficientes datos")

# Convertir a array numpy (grayscale 8 bits)
img = np.frombuffer(raw[:expected_size], dtype=np.uint8)
img = img.reshape((HEIGHT, WIDTH))

# Crear imagen
image = Image.fromarray(img, mode="L")
image.save(OUTPUT_FILE)

print(f"Imagen generada correctamente: {OUTPUT_FILE}")

El script nos devuelve un PNG válido pero con las letras torcidas. Tras darle vueltas me di cuenta de que si en el script usamos como WIDTH=1571 en lugar de 1570, la imagen resultante es correcta y tiene todo el sentido del mundo ya que 1571×74=116.254, que son exactamente los bytes que se encuentran antes del png señuelo.

Aunque el ancho visible de la imagen es de 1570 píxeles, cada fila ocupa realmente 1571 bytes. Ese byte adicional actúa como relleno (padding) y forma parte del stride o bytes por fila. Ignorar este detalle lleva a un desplazamiento erróneo acumulativo y por eso se ve la imagen torcida. En este caso concreto da igual ya que el texto se aprecia, pero si el reto hubiera sido más exigente no se vería nada.

por ·Sin comentarios

Table of Contents

Intro

Antes que nada, es importante saber que un archivo ELF en Linux es equivalente a un archivo EXE en Windows. Dicho esto, es bastante común encontrarnos con ejecutables ELF en diversos CTFs (Capture The Flag), y a menudo representan un desafío para aquellos no familiarizados con el uso cotidiano de Linux. Sin embargo, tengo una buena noticia si no eres aficionado de Linux: existen herramientas que permiten realizar un análisis preliminar para determinar si es necesario abordar el problema desde Linux o si podemos resolverlo directamente desde Windows. Estas herramientas facilitan una transición más cómoda para los usuarios de Windows, permitiéndoles interactuar eficazmente con archivos ELF.

ELF

Un archivo ELF (Executable and Linkable Format) es un formato común de archivo para archivos ejecutables, código objeto, bibliotecas compartidas y volcados de memoria en sistemas basados en Unix, como Linux. Es el estándar de formato de archivo para programas compilados y enlazados en este tipo de sistemas operativos.

La cabecera de un archivo ELF es una estructura de datos al comienzo del archivo que proporciona información esencial sobre el contenido y la forma de procesar el archivo. Esta cabecera es fundamental para que el sistema operativo y otros programas puedan interpretar correctamente el archivo ELF. Aquí están los componentes clave de la cabecera de un archivo ELF:

  1. Identificación (e_ident): Esta sección incluye la magia del archivo ELF, representada por los primeros cuatro bytes 0x7F 'E' 'L' 'F'. También incluye información como la clase del archivo (32 o 64 bits), la codificación de datos (endianness), y la versión del formato ELF.
  2. Tipo (e_type): Indica el tipo de archivo ELF, como EXEC (ejecutable), DYN (biblioteca compartida), REL (relocalizable), entre otros.
  3. Máquina (e_machine): Especifica la arquitectura de hardware para la cual se diseñó el archivo, por ejemplo, x86, ARM.
  4. Versión (e_version): La versión del formato ELF, generalmente establecida en 1.
  5. Punto de Entrada (e_entry): La dirección de memoria virtual donde comienza la ejecución del proceso.
  6. Desplazamiento del Program Header (e_phoff): Indica dónde comienza el encabezado del programa en el archivo.
  7. Desplazamiento del Section Header (e_shoff): Indica dónde comienza el encabezado de la sección en el archivo.
  8. Flags (e_flags): Banderas específicas del procesador.
  9. Tamaño de esta cabecera (e_ehsize): El tamaño de la cabecera ELF.
  10. Tamaño del Program Header (e_phentsize): El tamaño de una entrada del encabezado del programa.
  11. Número de entradas del Program Header (e_phnum): El número total de entradas en el encabezado del programa.
  12. Tamaño del Section Header (e_shentsize): El tamaño de una entrada del encabezado de la sección.
  13. Número de entradas del Section Header (e_shnum): El número total de entradas en el encabezado de la sección.
  14. Índice del Section Header Table (e_shstrndx): El índice del encabezado de la sección que contiene los nombres de las secciones.

El reto

Se nos proporciona un fichero de 20KB que rápidamente catalogamos como ELF.

Para realizar un análisis preliminar siempre uso DogBolt, que no es más que un decompilador online con la ventaja de que usa varios motores y de esta forma casi siempre te da una decompilación aceptable. La versión actual tiene disponibles 11 motores y además es open source, ¿Qué más se puede pedir?

Echamos un vistazo y enseguida encontramos algo interesante.

La flag parece codificada de modo que vamos a indagar acerca de la función FUN_0010285d

Dentro de la función FUN_0010285d vemos que nuestra flag codificada la procesa la función FUN_00102752

Aquí os diría que depende de vuestra experiencia en programación veríais que se está procesando byte a byte la cadena de entrada (param_1) y haciendo a cada byte un XOR (^) con el param_3 (que es 1 según vemos en la llamada de la función FUN_00102752), pero en estos tiempos que corren vamos a preguntar a ChatGPT que opina.

ChatGPT

Le pido a ChapGPT que me analice el código y me responde:

Este código en C define una función llamada FUN_00102752 que realiza una operación de XOR (exclusivo OR) byte a byte sobre un bloque de memoria. La función toma tres parámetros:

  1. long param_1: Este parámetro es tratado como una dirección de memoria. Se utiliza como la base de un bloque de memoria sobre el que se realizará la operación.
  2. ulong param_2: Este parámetro especifica el tamaño del bloque de memoria que será afectado por la operación.
  3. byte param_3: Este es el valor de un solo byte que se utilizará en la operación XOR.

El cuerpo de la función consiste en un bucle for que itera sobre el bloque de memoria:

  • int local_c se declara como una variable local y se inicializa en 0. Esta variable actúa como un contador para el bucle.
  • La condición del bucle (ulong)(long)local_c < param_2 asegura que el bucle se ejecute sobre el rango completo del bloque de memoria especificado por param_2.
  • Dentro del bucle, *(byte *)(param_1 + local_c) = *(byte *)(param_1 + local_c) ^ param_3; realiza la operación XOR. Aquí, *(byte *)(param_1 + local_c) accede al byte actual en el bloque de memoria. Este byte se modifica aplicándole un XOR con param_3. La operación XOR se realiza entre el byte actual en la memoria y el valor de param_3, y el resultado se escribe de nuevo en la misma ubicación de memoria.

En resumen, la función FUN_00102752 modifica un bloque de memoria aplicando una operación XOR con un valor dado (param_3) a cada byte dentro del rango de memoria especificado desde param_1 hasta param_1 + param_2. Este tipo de operación es común en tareas como la manipulación de datos para cifrado/descifrado o para la generación de patrones específicos en un bloque de datos.

by ChatGPT

Ahora imaginad que no sois muy dados a programar o simplemente estáis vagos de modo que volvemos a recurrir a ChatGPT con el promt «Haz un XOR 1 con javascript a la cadena: gmfzuihr^vr^o^drx^nod^shfiu|» a lo que responde:

function xorString(str) {
return Array.from(str).map(char => String.fromCharCode(char.charCodeAt(0) ^ 1)).join(»);
}

console.log(xorString(‘gmfzuihr^vr^o^drx^nod^shfiu|’));

by ChatGPT

Copiamos el código y lo pegamos en un entorno online como por ejemplo playcode.io.

Este es un ejemplo simple, pero ¿percibís su potencial?

La imagen de portada de esta entrada ha sido generada con ChatGPT.

por ·2 comentarios

Warning: This challenge is still active and therefore should not be resolved using this information.
Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.

Table of Contents

Intro

This crackme is for the challenge Mobile 2 of canyouhack.it.
This time you need to understand how the crackme works over the web.

Decompiling

The crackme is given again at Google Play, so the first step is to install and recover the APK for decompiling. The latter, I leave to you.
Open the victim with APK Studio and view the content of Mobile2.java
First we view one link:
http://canyouhack.it/Content/Challenges/Mobile/2/index.php
 If we go to the link, we view one string like a hash: 68a571bcf7bc9f76d43bf931f413ab2c. Umm, it’s like MD5. Go to decrypt online and we get the pass: «canyouhack.it». But if we test this password in the crackme, surprise!, nothing happens. We need to continue analyzing the code. Later we view the next interesting link:
«http://canyouhack.it/Content/Challenges/Mobile/2/submit.php?Token=» + Mobile2.token + «&Attempts=»
The program submit one token and concatenate with the number of attempts. Ok but what is the token and what is the number of attempts?
In this point we have to try with the information we already have.
Testing with the link of bottom we get “Nice try!” message. 
http://canyouhack.it/Content/Challenges/Mobile/2/submit.php?Token=68a571bcf7bc9f76d43bf931f413ab2c&&Attempts=0
Testing with the link of bottom we get “Very Good, the password is Top*****!” message. 
http://canyouhack.it/Content/Challenges/Mobile/2/submit.php?Token=68a571bcf7bc9f76d43bf931f413ab2c&&Attempts=1

  Links