Este crackme pertenece a la página de Karpoff Spanish Tutor. Data del año 2000 y está realizado en «Borland Delphi 6.0 – 7.0», además, para resolverlo deberemos activar un botón y conseguir la clave de registro. La principal dificultad proviene a la hora de activar el botón ya que el serial es en realidad un serial hardcodeado muy sencillo.
Activar un botón en memoria
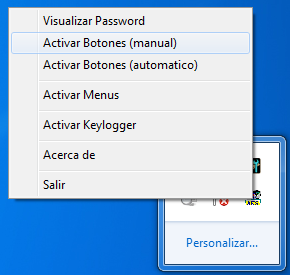
Existen numerosas herramientas para facilitarnos esta tarea, una de las más conocidas en el entorno del Cracking es «Veoveo» realizado por Crack el Destripador & Marmota hace ya unos añitos. Con el crackme ejecutado, ejecutamos VeoVeo y nos aparece el icono en la barra de tareas, hacemos click derecho y elegimos Activar Botones (manual) y ya tenemos el botón activado. Claro está que en cada ejecución del Crackme debemos de Re-activarlo.
Activar el botón de forma permanente
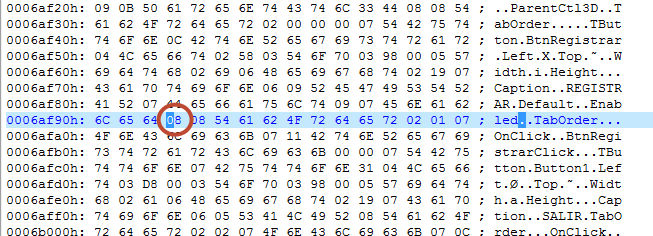
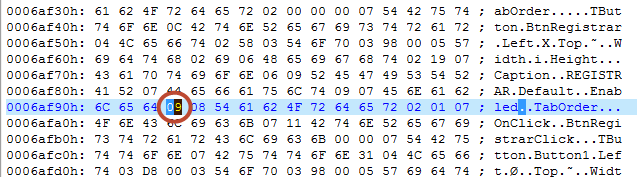
Lo que siempre nos interesa es que el botón esté activado de forma permanente y eso nos exige un poco más de atención. En este caso nos enfrentamos a Delphi y no nos sirve ni Resource Hacker ni Dede. Cuando nos encontramos en un punto muerto el último recurso siempre es realizar un programa en Delphi con un botón activado y otro desactivado y compararlos con un editor hexadecimal para saber que cambia. Si hacemos esto llegaremos a la conclusión de que en Delphi el bit que equivale a desactivado es 8 y ha activado es 9. Con este simple cambio ya tenemos el crackme parcheado. Comentar que en este caso el crackme no tiene ningún timer ni ninguna rutina que desactive el botón de forma periódica, este es el caso más simple.
Serial Hardcodeado
Abrimos Ollydbg y en las «String references» encontramos los mensajes de versión registrada, pinchamos sobre ellos y vemos a simple vista la zona de comprobación del serial. Como podéis observar, el serial se vé a simple vista.
0045811A |. B8 10824500 MOV EAX,CrackMe3.00458210 ; ASCII "ESCRIBE ALGO JOER"
0045811F |. E8 D889FDFF CALL CrackMe3.00430AFC
00458124 |. EB 5C JMP SHORT CrackMe3.00458182
00458126 |> 807D FF 4F CMP BYTE PTR SS:[EBP-1],4F - O
0045812A |. 75 56 JNZ SHORT CrackMe3.00458182
0045812C |. 807D FE 41 CMP BYTE PTR SS:[EBP-2],41 - A
00458130 |. 75 50 JNZ SHORT CrackMe3.00458182
00458132 |. 807D FD 45 CMP BYTE PTR SS:[EBP-3],45 - E
00458136 |. 75 4A JNZ SHORT CrackMe3.00458182
00458138 |. 807D FC 4B CMP BYTE PTR SS:[EBP-4],4B - K
0045813C |. 75 44 JNZ SHORT CrackMe3.00458182
0045813E |. 807D FB 43 CMP BYTE PTR SS:[EBP-5],43 - C
00458142 |. 75 3E JNZ SHORT CrackMe3.00458182
00458144 |. 807D FA 41 CMP BYTE PTR SS:[EBP-6],41 - A
00458148 |. 75 38 JNZ SHORT CrackMe3.00458182
0045814A |. 807D F9 52 CMP BYTE PTR SS:[EBP-7],52 - R
0045814E |. 75 32 JNZ SHORT CrackMe3.00458182
00458150 |. 807D F8 4B CMP BYTE PTR SS:[EBP-8],4B - K
00458154 |. 75 2C JNZ SHORT CrackMe3.00458182
00458156 |. 807D F7 20 CMP BYTE PTR SS:[EBP-9],20 -
0045815A |. 75 26 JNZ SHORT CrackMe3.00458182
0045815C |. 807D F6 49 CMP BYTE PTR SS:[EBP-A],49 - I
00458160 |. 75 20 JNZ SHORT CrackMe3.00458182
00458162 |. 807D F5 4F CMP BYTE PTR SS:[EBP-B],4F - O
00458166 |. 75 1A JNZ SHORT CrackMe3.00458182
00458168 |. 807D F4 54 CMP BYTE PTR SS:[EBP-C],54 - T
0045816C |. 75 14 JNZ SHORT CrackMe3.00458182
0045816E |. 807D F3 20 CMP BYTE PTR SS:[EBP-D],20 -
00458172 |. 75 0E JNZ SHORT CrackMe3.00458182
00458174 |. 807D F2 41 CMP BYTE PTR SS:[EBP-E],41 - A
00458178 |. 75 08 JNZ SHORT CrackMe3.00458182
0045817A |. 807D F1 59 CMP BYTE PTR SS:[EBP-F],59 - Y
0045817E |. 75 02 JNZ SHORT CrackMe3.00458182
00458180 |. B3 01 MOV BL,1
00458182 |> 80FB 01 CMP BL,1
00458185 |. 75 4C JNZ SHORT CrackMe3.004581D3
00458187 |. BA 2C824500 MOV EDX,CrackMe3.0045822C
0045818C |. 8B86 F4020000 MOV EAX,DWORD PTR DS:[ESI+2F4]
00458192 |. E8 B5EBFDFF CALL CrackMe3.00436D4C
00458197 |. BA 48824500 MOV EDX,CrackMe3.00458248 ; ASCII "VERSION REGISTRADA :)"
Serial = YA TOI KRACKEAO
Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.
Análisis inicial
El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.
Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.
Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.
Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.
ChatGPT
resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos
Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:
Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.
Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.
El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.
Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.
Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.
El código
Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.
soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)
for x in rango_valores_x:
for y in rango_valores_y:
for z in rango_valores_z:
# Calculamos el valor de la expresión para cada combinación de x, y, z
valor = x / (y + z) + y / (x + z) + z / (x + y)
# Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
if abs(valor - 4) < 1e-6: # Usamos una pequeña tolerancia para evitar errores de precisión
soluciones.append((x, y, z))
print(soluciones)
Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.
En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.
¿Qué está pasando?
Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.
Curvas elípticas
Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.
Adecuación
Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.
Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.
\begin{align}
& y^2=x^3+109x^2+224x\\
\end{align}
donde:
\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}
Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.
Mathematica
El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos.
(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva,
o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] :=
If[x1 == x2 && y1 == y2,
ImplicitD[curve4, y, x] /. {x -> x1, y -> y1},
(y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos
o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1;
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] :=
{Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2,
-Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] :=
{(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)),
(8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)),
(-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución
válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n,
NestWhile[nextRational4[#, P4] &, P4,
! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]
Solución
Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.
ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.
Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.
En esta ocasión vamos a hablar de una película de culto de los años 90, Hackers – Piratas Informáticos. La verdad es que aunque puede ser entretenida, tecnológicamente es una pesadilla y es que esta película es un claro ejemplo de cuando Hollywood prefiere agradar visualmente a representar escenas realistas.
Tras cuatro minutos en los que se nos presenta a Dade (Jonny Lee Miller) y sus problemas con la ley a una temprana edad, saltamos unos años después hasta ver a Dade encerrado en su habitación volviendo a las andadas intentando acceder ilegítimamente a los servidores de una cadena de televisión. Para ello hace uso de algo muy conocido en el mundillo Hacker, la Ingeniería Social, y es que aunque ahora disponemos de «cierta» conciencia en seguridad informática, en los años 90 no había ninguna. Bien, el caso es que Dade llama a las oficinas de la citada cadena de televisión a una hora en la que no hay más que el vigilante de seguridad y éste le proporciona un número que debemos suponer que es la IP de un Módem y comienza la intrusión.
BTM
Para empezar, se le ve al protagonista escribir comandos cuando en la pantalla no hay más que una animación en algo parecido a una ventana de terminal al estilo «Commander», pero no vemos lo que escribe, algo irreal.
A continuación y como por arte de magia entra en el sistema y lo que se muestra es una animación parpadeante con el logo de la compañia y el nombre del sistema al que estamos accediendo, también irreal.
Finalmente nos muestra sus intenciones, y son nada más y nada menos que cambiar la programación actual simplemente cambiando de VHS, inmejorable. A continuación os muestro la secuencia.
Por lo menos nos queda el consuelo de que cambia la tertulia de un tipejo con ciertos prejuicios raciales por una programación más interesante como «The Outer limits«, aquí conocida como «Más allá del límite«.
El resto de escenas informáticas de la película carecen de veracidad, la única que se salva, puede ser cuando accede al servidor del Instituto para programar el sistema contra incendios y vengarse de Kate (Angelina Jolie), ya que las imágenes que aparecen son de los primeros entornos gráficos de Mac.
Es extraño que casi todas las intrusiones las realiza desde su propia casa, algo poco inteligente, ya que por muy bueno que seas, siempre dejas huellas. Solo cuando se enfrentan a un Super-Hacker se empiezan a tomar las cosas en serio y realizan los ataques desde cabinas telefónicas.
En la película También hacen mención al Phreaking y a algunos de los libros que eran famosos por aquella época pero poco más que destacar. Por todo esto y mucho más, y aunque me caen igual de bien tanto Angelina como Jonny, la película se merece un majestuoso sello de BTM.
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
Realistic Challenge 3: Your school is employing a web designer who is charging far too much for site design and doesn’t know anything about protecting the site. However, he’s sure that there’s no way anyone can hack into any site he’s designed, prove him wrong!
En tu escuela están haciendo una web nueva muy rápido. El creador asegura que no le pueden hackear, demuéstrale que está equivocado.
Analizando a la víctima
Echamos un vistazo y vemos en el menú cosas interesantes. La primera de ellas es un Login que pronto descartamos ya que no parece llevar a ninguna parte. La segunda sirve para mandar enlaces al administrador y que este los publique posteriormente en la web.
Vamos a trastear un poco con la opción de mandar enlaces. En el código fuente ya vemos algo interesante y es que hay un campo oculto con el valor a 1 al mandar el enlace. Probamos a mandar un enlace sin tocar nada y nos dice que lo manda pero que lo tienen que aprobar. Vamos a probar ahora cambiando el valor del parámetro oculto a 0 con Firebug.
¡Funcionó!, el enlace ha pasado el filtro.
¿Cómo podemos aprovechar esto?, pués la forma más común es «XSS cross site scripting«. Veamos una prueba. Con el parámetro oculto otra vez en 0 mandamos el siguiente enlace y reto superado.
En Parque Jurásico (1993), la informática no es solo un elemento narrativo, es una pieza clave del suspense y del conflicto. A diferencia de otras películas donde las pantallas muestran interfaces ficticias o visualmente espectaculares pero irreales, Parque Jurásico opta por una aproximación sorprendentemente sobria y auténtica.
Durante bastantes escenas, se nos muestran terminales, ventanas de código y comandos que, lejos de ser decorativos, pertenecen a sistemas reales utilizados por programadores profesionales de principios de los años 90. Este detalle, que puede pasar desapercibido para el público general, resulta especialmente interesante desde un punto de vista técnico. En otras palabras, el trabajo de producción es excelente y destaca como una de las películas más respetuosas con la informática real de su época.
No es “código de película”: es software real
Uno de los puntos más interesantes es que el código que aparece en pantalla no fue escrito para la película. No hay pseudocódigo, ni pantallas diseñadas solo para quedar bonitas en cámara. Lo que se ve es software real, ejecutándose en el entorno Macintosh Programmer’s Workshop (MPW), el kit oficial de Apple para desarrolladores en aquellos años. El sistema operativo que se reconoce es un Macintosh clásico (System 7) corriendo sobre máquinas de la serie Quadra, auténticos pepinos para la época. Vamos, que cuando John Hammond decía aquello de «no hemos reparado en gastos», también iba en serio en lo informático.
«No hemos reparado en gastos»
En este punto no se le puede reprochar demasiado a la película. En líneas generales es bastante fiel a la novela, aunque la resolución del problema de seguridad se aborda de forma distinta. En el libro es el ingeniero Ray Arnold quien detecta el fallo y consigue reconducir la situación. En la película, sin embargo, el personaje desaparece cuando va a los barracones a restablecer la corriente del parque, con el resultado que todos conocemos.
Lo curioso es que muchos personajes sí cambian de forma notable con respecto al libro, el niño es mayor y más friki de los ordenadores, Ray Arnold no muere y acaba salvando la situación, o Gennaro es más atlético y bastante más valiente. Sin embargo, el gran disparate técnico permanece intacto.
En la novela se menciona de pasada a un equipo de informáticos de Cambridge que supuestamente colaboró en el diseño del software. Aun así, la puesta en marcha y la explotación del sistema recaen prácticamente en una sola persona, Dennis Nedry. Evidentemente, tanto al libro como al guion les viene de perlas que todo dependa de una única persona para que el desastre sea posible, pero cuesta aceptar que en un parque donde todo está duplicado, el control informático central dependa de una sola persona.
Curiosamente, en uno de los monitores de Nedry se puede ver una foto de Oppenheimer con la frase «Beginning of baby boom», de la que podemos sacar la conclusión de que Nedry es perfectamente consciente de que su trabajo puede tener consecuencias catastróficas e irreversibles. También es un maravilloso guiño del equipo de producción que nos está indicando exactamente donde se va originar el desastre.
Al final, Parque Jurásico no va de dinosaurios, ni siquiera de genética. Va de personas. Y, más concretamente, de personas con demasiado poder y muy pocos compañeros de equipo y poca supervisión.
Desde el punto de vista informático, la película es casi entrañable. Todo es serio, profesional y real… hasta que descubrimos que el sistema más complejo jamás construido depende, en la práctica, de un solo programador cabreado, mal pagado y con demasiadas líneas de código en la cabeza. Ningún comité de arquitectura, ninguna auditoría externa, ningún segundo par de ojos. Solo Dennis Nedry y su teclado. ¿Qué podía salir mal?
Lo curioso es que ni la película ni el libro se molestan en disimularlo demasiado. Te hablan de sistemas redundantes, de seguridad, de control absoluto… pero el corazón digital del parque es un castillo de naipes. Eso sí, un castillo de naipes programado en máquinas de primera, con software real y pantallas que hoy siguen pareciendo más creíbles que muchas producciones actuales.
Quizá por eso Parque Jurásico envejece tan bien. Porque, incluso cuando se equivoca, lo hace con honestidad. No intenta venderte magia disfrazada de tecnología. Te muestra ordenadores de verdad, código de verdad y errores muy humanos. Y al final, tanto en la novela como en la película, el mensaje es el mismo, puedes clonar dinosaurios, diseñar parques imposibles y rodearte de la mejor tecnología del mundo, que si todo depende de una sola persona, tarde o temprano, el sistema se vendrá abajo.
Y no, el problema no eran los dinosaurios, nunca lo fueron.
Hoy analizamos Copycat, un thriller psicológico de 1995 que, como muchas películas de la época, no pudo resistirse a incorporar elementos tecnológicos que, vistos desde una perspectiva actual, nos sacan una sonrisa. Vamos a desmontar algunos gazapos tecnológicos y curiosidades relacionadas con los sistemas informáticos que aparecen en la película.
El escritorio de tres pantallas: ¿el futuro en 1995?
La protagonista, la Dra. Helen Hudson (Sigourney Weaver), trabaja en un escritorio con tres pantallas, algo futurista para la época. En 1995, esto no era tan común como hoy en día. Para lograrlo, probablemente necesitaría tres ordenadores conectados de forma independiente, ya que los sistemas operativos y hardware de la época no solían soportar múltiples monitores en una sola máquina. Esto plantea preguntas interesantes sobre la logística de su set-up: ¿Cómo sincronizaba su trabajo entre tres PCs?
Un detalle curioso es que, en algunas tomas, se distingue la marca Compaq en los equipos. Compaq era una de las compañías líderes en la fabricación de ordenadores personales durante los 90 y conocida por sus soluciones de alta calidad. Este dato refuerza la idea de que el set-up de Helen estaba diseñado para representar lo último en tecnología de la época, aunque hoy resulte un tanto rudimentario. La elección de Compaq no es casual: en ese momento, era sinónimo de equipos potentes, usados tanto en oficinas como en entornos domésticos avanzados.
Internet y la magia de los módems
En una escena, Helen navega por internet con lo que suponemos es un módem de 28.8 kbps (o como mucho, un flamante 33.6 kbps, tecnología de vanguardia allá por 1995). Hasta ahí, vale. Sin embargo, la fluidez de su conexión sorprende: carga archivos, recibe correos y no se queda esperando con una pantalla de “Conectando…”. Pero lo mejor llega cuando, estando conectada, ¡suena el teléfono! En la realidad, esto cortaría la conexión o comunicaría, a menos que tuviera dos líneas telefónicas (algo raro en domicilios particulares de la época) o algún dispositivo milagroso que no conocemos.
¿Qué sistema operativo usa?
Aunque no se distingue claramente el sistema operativo, vemos una interfaz gráfica con ventanas y una consola de comandos. Esto podría ser un guiño a Windows 3.1 o Windows 3.11, ya maduro en esa época aunque la interfaz no termina de encajar. Sin embargo, también podría ser una mezcla ficticia para hacer que el entorno luciera “tecnológico” sin comprometerse demasiado con la realidad. Detalle curioso: en los 90, las películas solían personalizar las interfaces para no tener problemas legales.
El email como el epicentro de la tecnología
En los 90, el email era el rey. En las películas, los escritorios siempre tenían un gran icono de correo (a menudo animado, porque lo cool siempre parpadeaba). En Copycat, Helen recibe un correo con un archivo AVI de unos 30 segundos, lo cual plantea otra duda técnica: ¿Cuánto espacio ocupaba ese archivo en 1995?
Un AVI de 30 segundos probablemente tendría una resolución baja (320×240 píxeles o menos) y una tasa de compresión eficiente para la época, pero aun así podría pesar entre 2 y 5 MB, dependiendo de la calidad del audio y vídeo. Eso hubiera supuesto una odisea por email, ya que los servidores de la época limitaban los adjuntos a unos pocos cientos de KB. ¿Quizás el villano usó un protocolo privado para saltarse las restricciones?
Tomorrow.AVI
Tras recibir un inquietante archivo AVI, la protagonista llama a la policía, lo que desencadena una conversación cargada de decisiones tecnológicas cuestionables:
«¿Cómo le han enviado esto?» / «Consiguiendo su dirección de internet»: El archivo es descrito como enviado a través de «su dirección de internet», un término extraño para la época en la que lo habitual habría sido referirse al correo electrónico. Esto refleja un intento de sonar sofisticado sin usar los términos correctos.
«¿No podríamos localizarlo?»: La respuesta de los policías es que no pueden rastrear el origen del archivo «a no ser que esté conectado». Sin embargo, incluso en 1995, las cabeceras de los emails contenían suficiente información para rastrear el servidor de origen, aunque la práctica era más rudimentaria que en la actualidad. Ignorar esto parece una licencia creativa del guion o un concepto equivocado de localizar asociándolo quizá a las llamadas telefónicas.
«Es demasiado grande para pasarlo a disco»: Aquí surge el principal obstáculo: el archivo AVI es considerado «demasiado grande» para transferirlo a un disquete de 3,5 pulgadas (con una capacidad máxima de 1,44 MB). Aunque esto tiene sentido desde una perspectiva técnica, resulta extraño que fuera posible enviarlo por email en primer lugar, dado que los servidores de correo de la época tenían limitaciones más estrictas que un disquete. Esto sugiere una inconsistencia en la lógica tecnológica de la escena.
«Lo pasaremos a vídeo»: Ante la imposibilidad de transferirlo a un disquete, la solución propuesta es convertir el archivo a un formato reproducible en un dispositivo analógico (probablemente una cinta VHS) para transportarlo físicamente. Aunque esta decisión es plausible dentro de las limitaciones tecnológicas de la época, omite soluciones más digitales, como volver a enviarlo por email (¿acaso la policía no tenía correo electrónico?). Además, surge la pregunta de por qué no se recurre a los forenses técnicos de la policía (o del FBI) para analizar el disco duro, quienes, curiosamente, no aparecen en ningún momento de la película.
«Oh, Dios. ¿Cómo sabes todas estas cosas?» / «Malgasté mi juventud en los salones de videojuegos»: Esta frase añade un toque humorístico, pero no tiene relación alguna con las habilidades necesarias para resolver el problema en cuestión. Más bien, refuerza la desconexión entre los diálogos y las acciones tecnológicas presentadas.
Conclusión
Copycat (1995) es un buen ejemplo de cómo el cine de los 90 abordaba la tecnología con una mezcla de admiración y confusión. Desde la exageración de tener tres monitores en el escritorio de Helen hasta la torpe gestión del archivo Tomorrow.AVI, la película refleja tanto las limitaciones tecnológicas de la época como las libertades creativas de los guionistas.
En el caso del archivo AVI, los personajes deciden que no se puede gestionar digitalmente y optan por convertirlo a vídeo analógico, ignorando soluciones más simples como volver a enviarlo por correo electrónico (suponiendo que fuera posible). Este detalle, combinado con la ausencia aparente de personal técnico en la policía, subraya una desconexión entre la narrativa y las capacidades reales de la tecnología, incluso para 1995.
Aunque estos detalles pueden parecer cómicos 30 años después, forman parte del encanto de un cine que imaginaba el futuro sin comprender del todo su presente. Más que errores, son un recordatorio de cómo la tecnología ha evolucionado y de cómo nuestra percepción de ella también lo ha hecho.
