Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
Intro
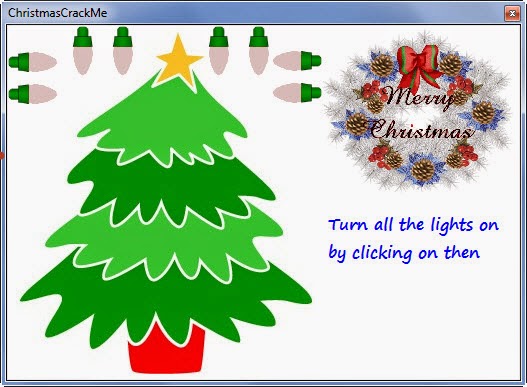
This crackme is for the crack challenge 6 of canyouhack.it.
In this crackme the goal is to turn on all the lights. Note that a light off to the next, so if we interrupt this, we win.
Tools
Exeinfo (For crackme info)
Delphi Decompiler (For decompile)
OllyDbg (For debug)
Decompiling
With Delphi Decompiler we can found easy the buttons and his offsets.
Go to the offset 401A64 in OllyDbg and analyze the code.
We view two jumps, one turn ON the light and the other Turn OFF the next light. Patching the call from offset 401A8B we get the serial.
Hoy vamos a enfrentarnos a cuatro retos de esteganografía relativamente sencillos, y digo relativamente, debido a que hay tantas formas de esconder información en un archivo, ya sea imagen, vídeo o sonido, que afrontarlos suele ser desesperante. Las cuatro imágenes son aparentemente las mismas que la que se ve en portada.
Una buena práctica cuando te enfrentas a retos stego de tipo imagen es realizar una búsqueda inversa. Una búsqueda inversa consiste en buscar la imagen original mediante buscadores especializados como TinEye o Google. Si conseguimos la imagen original podemos resolver el reto simplemente comparando o nos puede dar una idea del tipo de modificación por su diferencia de tamaño, colores, degradados, etc.
Stego 1
Descargamos la imagen del reto. Se trata de una imagen JPEG de 526×263 y 76.6 KB (78445 bytes). Su hash SHA1 es «89aed5bbc3542bf5c60c4c318fe99cb1489f267a«
Realizamos una búsqueda inversa de la imagen y encontramos sin dificultad la imagen original mediante TinEye.
Por lo que vemos ha cambiado el tamaño de 78447 bytes a 78445 bytes y su hash SHA1 tampoco coincide obviamente, lo que nos confirma que ha sufrido alguna modificación. Echando un vistazo con un editor hexadecimal te puedes volver loco por lo que vamos a realizar una comparación mediante la herramienta online DiffNow.
Al realizar la comparación sale a relucir lo que buscamos. La clave es una simple cadena de texto.
Stego 2
Lo primero es realizar de nuevo la comparación.
Imagen
Tamaño
SHA1
Original
78447 bytes
8924676317077fc07c252ddeec04bd2a0ecfdda4
imagen2.jpeg
116386 bytes
7641e3906f795c137269cefef29f30fcb9cb1b07
Como vemos, la imagen ha aumentado significativamente, de 76,6 KB a 113 KB. Cuando el aumento de tamaño llama la atención normalmente tenemos otro archivo insertado. Lo primero que suelo hacer yo es fijarme si ha sido modificado el final del archivo con un editor hexadecimal. Los bytes de cola de un archivo jpg/jpeg son FFD9 y en este caso no vemos modificación alguna al final del archivo. Si el archivo no está al final requiere realizar una búsqueda más exhaustiva. Para estos casos tengo una herramienta de creación propia que se llama Ancillary y que sirve para buscar cierto tipo de archivos dentro de otros como imágenes, documentos de Office, Open Office, pdf, etc. Ancillary encuentra otro jpg que es el que le daba el peso extra y que vemos a continuación. La clave es el título de la película (ojo a las mayúsculas/minúsculas).
Stego 3
El tercer reto parece que tiene algún error debido a que el archivo coincide completamente con el original. Pienso que se ha subido la imagen original por error. Se lo he comunicado al admin del dominio y si algún día obtengo respuesta actualizaré la entrada.
Imagen
Tamaño
SHA1
Original
78447 bytes
8924676317077fc07c252ddeec04bd2a0ecfdda4
imagen3.jpeg
78447 bytes
8924676317077fc07c252ddeec04bd2a0ecfdda4
Actualización 21/08/2016
Al parecer, la solución de este reto es llegar a la conclusión de que la imagen no está modificada. La respuesta del Administrador de la web así lo confirma.
desingsecurity [at] gmail [dot] com – Sorry about the delay, is precisely what is intended with that challenge, they can determine if the image is changed or not , the challenge was solved you . We’ll be equal way improving this point.
Greetings and Thanks
Stego 4
Lo primero es realizar de nuevo la comparación.
Imagen
Tamaño
SHA1
Original
78447 bytes
8924676317077fc07c252ddeec04bd2a0ecfdda4
imagen4.jpeg
93174 bytes
a6329ea4562ef997e5afd067f3b53bdab4665851
Al igual que en el caso dos el tamaño ha aumentado significativamente de modo que miramos al final del archivo y esta vez si vemos que hay insertado unos bytes tras el final del jpg (recordemos FFD9)
El archivo tiene pinta de ser una hoja de cálculo de Open Office o Libre Office según indica la palabra «spreadsheet«. Lo abrimos con Excel y tras analizar la maraña de datos enseguida vemos una clave que llama la atención.
Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.
Análisis inicial
El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.
Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.
Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.
Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.
ChatGPT
resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos
Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:
Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.
Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.
El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.
Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.
Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.
El código
Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.
soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)
for x in rango_valores_x:
for y in rango_valores_y:
for z in rango_valores_z:
# Calculamos el valor de la expresión para cada combinación de x, y, z
valor = x / (y + z) + y / (x + z) + z / (x + y)
# Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
if abs(valor - 4) < 1e-6: # Usamos una pequeña tolerancia para evitar errores de precisión
soluciones.append((x, y, z))
print(soluciones)
Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.
En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.
¿Qué está pasando?
Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.
Curvas elípticas
Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.
Adecuación
Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.
Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.
\begin{align}
& y^2=x^3+109x^2+224x\\
\end{align}
donde:
\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}
Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.
Mathematica
El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos.
(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva,
o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] :=
If[x1 == x2 && y1 == y2,
ImplicitD[curve4, y, x] /. {x -> x1, y -> y1},
(y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos
o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1;
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] :=
{Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2,
-Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] :=
{(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)),
(8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)),
(-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución
válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n,
NestWhile[nextRational4[#, P4] &, P4,
! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]
Solución
Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.
ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.
Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.
Hoy analizamos Copycat, un thriller psicológico de 1995 que, como muchas películas de la época, no pudo resistirse a incorporar elementos tecnológicos que, vistos desde una perspectiva actual, nos sacan una sonrisa. Vamos a desmontar algunos gazapos tecnológicos y curiosidades relacionadas con los sistemas informáticos que aparecen en la película.
El escritorio de tres pantallas: ¿el futuro en 1995?
La protagonista, la Dra. Helen Hudson (Sigourney Weaver), trabaja en un escritorio con tres pantallas, algo futurista para la época. En 1995, esto no era tan común como hoy en día. Para lograrlo, probablemente necesitaría tres ordenadores conectados de forma independiente, ya que los sistemas operativos y hardware de la época no solían soportar múltiples monitores en una sola máquina. Esto plantea preguntas interesantes sobre la logística de su set-up: ¿Cómo sincronizaba su trabajo entre tres PCs?
Un detalle curioso es que, en algunas tomas, se distingue la marca Compaq en los equipos. Compaq era una de las compañías líderes en la fabricación de ordenadores personales durante los 90 y conocida por sus soluciones de alta calidad. Este dato refuerza la idea de que el set-up de Helen estaba diseñado para representar lo último en tecnología de la época, aunque hoy resulte un tanto rudimentario. La elección de Compaq no es casual: en ese momento, era sinónimo de equipos potentes, usados tanto en oficinas como en entornos domésticos avanzados.
Internet y la magia de los módems
En una escena, Helen navega por internet con lo que suponemos es un módem de 28.8 kbps (o como mucho, un flamante 33.6 kbps, tecnología de vanguardia allá por 1995). Hasta ahí, vale. Sin embargo, la fluidez de su conexión sorprende: carga archivos, recibe correos y no se queda esperando con una pantalla de “Conectando…”. Pero lo mejor llega cuando, estando conectada, ¡suena el teléfono! En la realidad, esto cortaría la conexión o comunicaría, a menos que tuviera dos líneas telefónicas (algo raro en domicilios particulares de la época) o algún dispositivo milagroso que no conocemos.
¿Qué sistema operativo usa?
Aunque no se distingue claramente el sistema operativo, vemos una interfaz gráfica con ventanas y una consola de comandos. Esto podría ser un guiño a Windows 3.1 o Windows 3.11, ya maduro en esa época aunque la interfaz no termina de encajar. Sin embargo, también podría ser una mezcla ficticia para hacer que el entorno luciera “tecnológico” sin comprometerse demasiado con la realidad. Detalle curioso: en los 90, las películas solían personalizar las interfaces para no tener problemas legales.
El email como el epicentro de la tecnología
En los 90, el email era el rey. En las películas, los escritorios siempre tenían un gran icono de correo (a menudo animado, porque lo cool siempre parpadeaba). En Copycat, Helen recibe un correo con un archivo AVI de unos 30 segundos, lo cual plantea otra duda técnica: ¿Cuánto espacio ocupaba ese archivo en 1995?
Un AVI de 30 segundos probablemente tendría una resolución baja (320×240 píxeles o menos) y una tasa de compresión eficiente para la época, pero aun así podría pesar entre 2 y 5 MB, dependiendo de la calidad del audio y vídeo. Eso hubiera supuesto una odisea por email, ya que los servidores de la época limitaban los adjuntos a unos pocos cientos de KB. ¿Quizás el villano usó un protocolo privado para saltarse las restricciones?
Tomorrow.AVI
Tras recibir un inquietante archivo AVI, la protagonista llama a la policía, lo que desencadena una conversación cargada de decisiones tecnológicas cuestionables:
«¿Cómo le han enviado esto?» / «Consiguiendo su dirección de internet»: El archivo es descrito como enviado a través de «su dirección de internet», un término extraño para la época en la que lo habitual habría sido referirse al correo electrónico. Esto refleja un intento de sonar sofisticado sin usar los términos correctos.
«¿No podríamos localizarlo?»: La respuesta de los policías es que no pueden rastrear el origen del archivo «a no ser que esté conectado». Sin embargo, incluso en 1995, las cabeceras de los emails contenían suficiente información para rastrear el servidor de origen, aunque la práctica era más rudimentaria que en la actualidad. Ignorar esto parece una licencia creativa del guion o un concepto equivocado de localizar asociándolo quizá a las llamadas telefónicas.
«Es demasiado grande para pasarlo a disco»: Aquí surge el principal obstáculo: el archivo AVI es considerado «demasiado grande» para transferirlo a un disquete de 3,5 pulgadas (con una capacidad máxima de 1,44 MB). Aunque esto tiene sentido desde una perspectiva técnica, resulta extraño que fuera posible enviarlo por email en primer lugar, dado que los servidores de correo de la época tenían limitaciones más estrictas que un disquete. Esto sugiere una inconsistencia en la lógica tecnológica de la escena.
«Lo pasaremos a vídeo»: Ante la imposibilidad de transferirlo a un disquete, la solución propuesta es convertir el archivo a un formato reproducible en un dispositivo analógico (probablemente una cinta VHS) para transportarlo físicamente. Aunque esta decisión es plausible dentro de las limitaciones tecnológicas de la época, omite soluciones más digitales, como volver a enviarlo por email (¿acaso la policía no tenía correo electrónico?). Además, surge la pregunta de por qué no se recurre a los forenses técnicos de la policía (o del FBI) para analizar el disco duro, quienes, curiosamente, no aparecen en ningún momento de la película.
«Oh, Dios. ¿Cómo sabes todas estas cosas?» / «Malgasté mi juventud en los salones de videojuegos»: Esta frase añade un toque humorístico, pero no tiene relación alguna con las habilidades necesarias para resolver el problema en cuestión. Más bien, refuerza la desconexión entre los diálogos y las acciones tecnológicas presentadas.
Conclusión
Copycat (1995) es un buen ejemplo de cómo el cine de los 90 abordaba la tecnología con una mezcla de admiración y confusión. Desde la exageración de tener tres monitores en el escritorio de Helen hasta la torpe gestión del archivo Tomorrow.AVI, la película refleja tanto las limitaciones tecnológicas de la época como las libertades creativas de los guionistas.
En el caso del archivo AVI, los personajes deciden que no se puede gestionar digitalmente y optan por convertirlo a vídeo analógico, ignorando soluciones más simples como volver a enviarlo por correo electrónico (suponiendo que fuera posible). Este detalle, combinado con la ausencia aparente de personal técnico en la policía, subraya una desconexión entre la narrativa y las capacidades reales de la tecnología, incluso para 1995.
Aunque estos detalles pueden parecer cómicos 30 años después, forman parte del encanto de un cine que imaginaba el futuro sin comprender del todo su presente. Más que errores, son un recordatorio de cómo la tecnología ha evolucionado y de cómo nuestra percepción de ella también lo ha hecho.
