por ·Sin comentarios

En esta ocasión vamos a hablar de una película de culto de los años 90, Hackers – Piratas Informáticos. La verdad es que aunque puede ser entretenida, tecnológicamente es una pesadilla y es que esta película es un claro ejemplo de cuando Hollywood prefiere agradar visualmente a representar escenas realistas.

Tras cuatro minutos en los que se nos presenta a Dade (Jonny Lee Miller) y sus problemas con la ley a una temprana edad, saltamos unos años después hasta ver a Dade encerrado en su habitación volviendo a las andadas intentando acceder ilegítimamente a los servidores de una cadena de televisión. Para ello hace uso de algo muy conocido en el mundillo Hacker, la Ingeniería Social, y es que aunque ahora disponemos de «cierta» conciencia en seguridad informática, en los años 90 no había ninguna. Bien, el caso es que Dade llama a las oficinas de la citada cadena de televisión a una hora en la que no hay más que el vigilante de seguridad y éste le proporciona un número que debemos suponer que es la IP de un Módem y comienza la intrusión.

BTM

Para empezar, se le ve al protagonista escribir comandos cuando en la pantalla no hay más que una animación en algo parecido a una ventana de terminal al estilo «Commander», pero no vemos lo que escribe, algo irreal.

vlcsnap-2015-11-25-18h00m25s936

A continuación y como por arte de magia entra en el sistema y lo que se muestra es una animación parpadeante con el logo de la compañia y el nombre del sistema al que estamos accediendo, también irreal.

vlcsnap-2015-11-25-12h43m18s762

Finalmente nos muestra sus intenciones, y son nada más y nada menos que cambiar la programación actual simplemente cambiando de VHS, inmejorable. A continuación os muestro la secuencia.

Por lo menos nos queda el consuelo de que cambia la tertulia de un tipejo con ciertos prejuicios raciales por una programación más interesante como «The Outer limits«, aquí conocida como «Más allá del límite«.

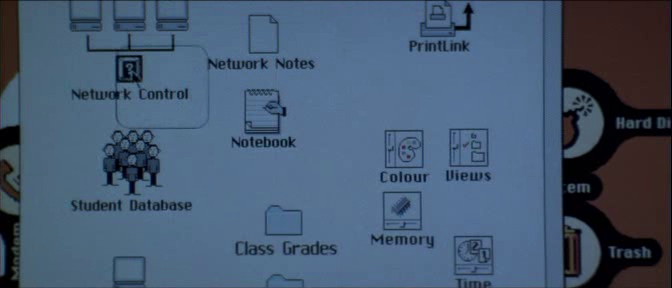
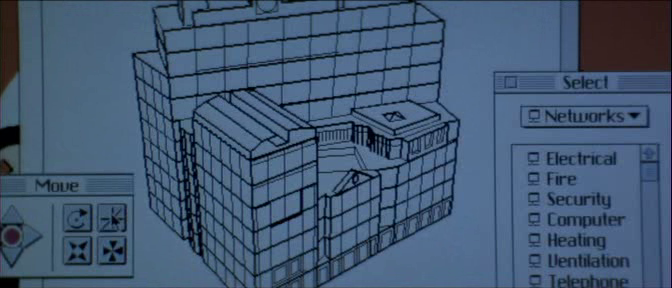
El resto de escenas informáticas de la película carecen de veracidad, la única que se salva, puede ser cuando accede al servidor del Instituto para programar el sistema contra incendios y vengarse de Kate (Angelina Jolie), ya que las imágenes que aparecen son de los primeros entornos gráficos de Mac.

vlcsnap-2015-11-25-18h29m08s043

vlcsnap-2015-11-25-18h29m15s390

vlcsnap-2015-11-25-18h29m31s550

Es extraño que casi todas las intrusiones las realiza desde su propia casa, algo poco inteligente, ya que por muy bueno que seas, siempre dejas huellas. Solo cuando se enfrentan a un Super-Hacker se empiezan a tomar las cosas en serio y realizan los ataques desde cabinas telefónicas.

En la película También hacen mención al Phreaking y a algunos de los libros que eran famosos por aquella época pero poco más que destacar. Por todo esto y mucho más, y aunque me caen igual de bien tanto Angelina como Jonny, la película se merece un majestuoso sello de BTM.

hackers_sello

Enlaces

Descargar contenido multimedia de ciertas webs
Hoy en día, la descarga de contenido multimedia de ciertas webs es imposible o muy difícil. En ciertos casos lo
ThisIsLegal.com - User Challenge 1 (Javascript)
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en
Canyouhack.it - Cryptography Challenge 13
Los retos criptográficos son muy variados y muchas veces la dificultad está en saber a que te enfrentas. En este
Wechall Stegano Attachment (Esteganografía)
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en

por ·1 comentario

Hoy en día, la descarga de contenido multimedia de ciertas webs es imposible o muy difícil. En ciertos casos lo entiendo, exponer el contenido supone una pérdida de ingresos y eso es inaceptable. Las cadenas de TV son tema aparte, emiten contenido por varios medios y les gusta que lo veas y que lo compartas, eso sí, que lo compartas desde su plataforma, ya que lo que estás compartiendo es un enlace, no el vídeo.

Este caso es un caso intermedio entre una plataforma de pago que codifica sus contenidos y una web que nos permita descargar su contenido directamente.

Imaginemos que vemos un vídeo y queremos mandarlo por Whatsapp a nuestros amigos. Lo primero es echar un vistazo al código fuente de la web y localizar el código del reproductor web (player). Para esta tarea podemos ayudarnos de una extensión muy conocida para navegadores como es Firebug. Una vez instalada, la activamos con F12 y mediante el botón Inspect localizamos el player.

...    
<p itemprop="keywords" itemscope="itemscope" itemtype="http://schema.org/Text" class="antetitulo" lang="es">EL INTERMEDIO LE PILLA EN "EL TRONO"</p>
    <h1 class="title-new" itemprop="headline">Joaquín Reyes se mete en la piel de Juan Carlos I: "Soy tan campechano que podéis llamarme Juan Carlos Palote"</h1>
    <sumary class="entradilla" itemprop="description">
<p><p class="MsoNormal">Los reyes eméritos han celebrado sus bodas de esmeralda y
con motivo de tan señalada fecha, Juan Carlos I ha hecho un hueco en su
apretada agenda para concederle unos minutos a <a title="<b>El Intermedio</b>" href="http://www.lasexta.com/temas/el_intermedio-1" target="_blank"><b>El Intermedio</b></a>. Eso sí, en su
versión de <a title="<b>Joaquín Reyes</b>" href="http://www.lasexta.com/temas/joaquin_reyes-1" target="_blank"><b>Joaquín Reyes</b></a>.  <o:p></o:p></p>	</sumary>

	<div class="great-element-multimedia">
	    <section class="modVideo a3mod_player" data-mod="a3mod_player" data-model="/json/video/7/2017/05/15/591a08c1986b2810b31577c1.json">
	        <a itemprop="url" href="#" class="icon link-content" title="" data-mod-elem="icon">
	            <div class="wrap-img" role="banner">
	                <div itemprop="video" itemscope itemtype="http://schema.org/VideoObject">
	                    <picture>
	                        <!--[if IE 9]><video style="display: none;"><![endif]-->
	                        <source media="(max-width:520px)" srcset="http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/64.jpg" />
	                        <source media="(max-width:1023px)" srcset="http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/60.jpg" />
	                        <source media="(min-width:1024px)" srcset="http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/58.jpg" />
	                        <!--[if IE 9]></video><![endif]-->
								<img src="http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/58.jpg" alt="Joaquín Reyes, como el rey Juan Carlos I" title="Joaquín Reyes, como el rey Juan Carlos I" />
	                    </picture>
	                    <meta itemprop="description" content=""/>
	                    <meta itemprop="name" content=""/>
	                    <meta itemprop="thumbnailUrl" content="" />
	                    <meta itemprop="uploadDate" content=""/>
	                    <meta itemprop="url" content=""/>
	                    <meta itemprop="width" content=""/>
	                    <meta itemprop="height" content=""/>
	                </div>
	            </div>
	        </a>
	    </section>
	</div>
...

Si os fijáis bien, el reproductor hace referencia a un archivo json (591a08c1986b2810b31577c1.json), reconstruimos la url y miramos su contenido

{"id":"591a08c1986b2810b31577c1","type":"video","tipo":"video","subtipo":"video","imgThumb":"http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/29.jpg","imgPoster":"http://fotografias.lasexta.com/clipping/cmsimages02/2017/05/15/14069ECA-B0E4-4F09-A5B7-04B600C016AD/31.jpg","live":false,"autoplay":true,"sources":[{"src":"http://vclip.atresmedia.com/vclip/_definst_/smil:assets10/2017/05/15/01229E28-A57E-4AC9-AFE7-EF1C27B5AA2A/es.smil/manifest_mvlist.mpd","type":"application/dash+xml"},{"src":"http://vclip.atresmedia.com/vclip/_definst_/smil:assets10/2017/05/15/01229E28-A57E-4AC9-AFE7-EF1C27B5AA2A/es.smil/playlist.m3u8","type":"application/vnd.apple.mpegurl"}],"omniture":{"section":"Joaquín Reyes","category":"El Intermedio","channel":"lasexta","type":"short","name":"Joaquín Reyes se mete en la piel de Juan Carlos I: \"Soy tan campechano que podéis llamarme Juan Carlos Palote\"","embeddedMode":false},"comscore":{"comscoreTag":"LASEXTA.COM","channel":"lasexta","kantar":{"programID":"1019","firstBroadcastDate":"*null","firstBroadcastTime":"*null","typeTvStream":"0002","kantarGenre":"0","channelId":"240"},"content_form":"short_form"},"urlHits":"http://hits.lasexta.com/l6//591a08c1986b2810b31577c1/3/348128,351435,351827,351865/","duration":"211.797333","embeddedUrl":"<iframe src=\"http://www.lasexta.com/embed/el-intermedio-le-pilla-en-el-trono/video/7/2017/05/15/591a08c1986b2810b31577c1\" width=\"560\" height=\"315\" frameborder=\"0\" allowfullscreen></iframe>","playondraw":true,"nextRelated":{"service_url":"http://www.lasexta.com/json/video/7/2017/05/15/591a08c1986b2810b31577c1_related.json"},"subtitle":[],"titulo":"Joaquín Reyes se mete en la piel de Juan Carlos I: \"Soy tan campechano que podéis llamarme Juan Carlos Palote\"","descripcion":"","sociales":{"hasTwitter":true,"hasFacebook":true,"hasGooglePlus":true,"hasWhatsapp":true,"twitter":"EL INTERMEDIO LE PILLA EN “EL TRONO”","facebook":"EL INTERMEDIO LE PILLA EN “EL TRONO”","googlePlus":"EL INTERMEDIO LE PILLA EN “EL TRONO”","whatsapp":"","hashtag":"","via":"sextaNoticias","urlPage":"https://goo.gl/cu98f0"},"vp_data":{"vp_category":"Atresmedia/Lasexta/programas/el-intermedio*","vp_tags":"","vp_content_form":"short_form"}}

Se puede ver a simple vista una lista de reproducción playlist.m3u8, cuyo contenido contiene más listas de reproducción con diferentes calidades.

#EXTM3U
#EXT-X-VERSION:3
#EXT-X-STREAM-INF:BANDWIDTH=796400,CODECS="avc1.77.30,mp4a.40.5",RESOLUTION=640x360
chunklist_b724000.m3u8
#EXT-X-STREAM-INF:BANDWIDTH=1159400,CODECS="avc1.77.30,mp4a.40.5",RESOLUTION=640x360
chunklist_b1054000.m3u8
#EXT-X-STREAM-INF:BANDWIDTH=1643400,CODECS="avc1.77.30,mp4a.40.5",RESOLUTION=720x404
chunklist_b1494000.m3u8
#EXT-X-STREAM-INF:BANDWIDTH=2248400,CODECS="avc1.77.31,mp4a.40.5",RESOLUTION=1280x720
chunklist_b2044000.m3u8

Reconstruimos la URL para la lista de reproducción de mayor calidad e inspeccionamos su contenido.

#EXTM3U
#EXT-X-VERSION:3
#EXT-X-TARGETDURATION:10
#EXT-X-MEDIA-SEQUENCE:0
#EXTINF:10.0,
media_b2044000_0.ts
#EXTINF:10.0,
media_b2044000_1.ts
#EXTINF:10.0,
media_b2044000_2.ts
#EXTINF:10.0,
media_b2044000_3.ts
#EXTINF:10.0,
media_b2044000_4.ts
#EXTINF:10.0,
media_b2044000_5.ts
#EXTINF:10.0,
media_b2044000_6.ts
#EXTINF:10.0,
media_b2044000_7.ts
#EXTINF:10.0,
media_b2044000_8.ts
#EXTINF:10.0,
media_b2044000_9.ts
#EXTINF:10.0,
media_b2044000_10.ts
#EXTINF:10.0,
media_b2044000_11.ts
#EXTINF:10.0,
media_b2044000_12.ts
#EXTINF:10.0,
media_b2044000_13.ts
#EXTINF:10.0,
media_b2044000_14.ts
#EXTINF:10.0,
media_b2044000_15.ts
#EXTINF:10.0,
media_b2044000_16.ts
#EXTINF:10.0,
media_b2044000_17.ts
#EXTINF:10.0,
media_b2044000_18.ts
#EXTINF:10.0,
media_b2044000_19.ts
#EXTINF:10.0,
media_b2044000_20.ts
#EXTINF:1.92,
media_b2044000_21.ts
#EXT-X-ENDLIST

Se pueden ver 21 archivos con extensión TS de 10 segundos cada uno a excepción del último que dura 1.92 segundos. Los archivos TS no son más que archivos MP4 por lo que una vez descargados, los podemos unir con MP4Tools por ejemplo.

La tarea es costosa, pero si os apetece enviar un vídeo en vez de un enlace, ya sabéis que en determinados casos se puede hacer.

por ·Sin comentarios

Warning: This challenge is still active and therefore should not be resolved using this information.
Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.

Introducción

 Este es el típico reto de Javascript, no tiene mucha complicación pero he decidido dedicarle una entrada por que me llamó la atención lo que utiliza de usuario y clave.

El Script

function getStyle(el,styleProp)
{
    var x = document.getElementById(el);
    if (x.currentStyle)
        var y = x.currentStyle[styleProp];
    else if (window.getComputedStyle)
        var y = document.defaultView.getComputedStyle(x,null).getPropertyValue(styleProp);

if (y.substr(0, 1) == "#"){ return y; } else {
    
var value = y.split(',');

var R = value[0].substr(4);
var G = value[1];
var B = value[2].substr(0, value[2].length-1);

var RGB =  "#" + toHex(R)+ toHex(G)+toHex(B);

return RGB;

 }
}

function toHex(N) {
 if (N==null) return "00";
 N=parseInt(N); if (N==0 || isNaN(N)) return "00";
 N=Math.max(0,N); N=Math.min(N,255); N=Math.round(N);
 return "0123456789ABCDEF".charAt((N-N%16)/16)
      + "0123456789ABCDEF".charAt(N%16);
}

function pw (form)
{

   var d1, d2, d3;

if (navigator.appName == "Netscape"){
   d1= getStyle('content', 'background-color');
} else {
   d1= getStyle('content', 'backgroundColor');
}

     d2=form.Name.value;
     d3=form.Password.value;

  if (d2==d1.length) {
    if (d3==d1) {
      window.open ("../" + d1.substr(1, 10), "_self")
    } else {
      alert("Muhaha! Wrong!")
    }
  } else {
    alert("Muhaha! Wrong!")
  }
}

El Formulario

<div class="chal_box" style="padding:10px;">
<form name="form" action="" method="post">
        Username<br />
        <input id="inputd2" type="text" name="Name" value="" size="30" maxlength="30"><br />
        Password<br />
        <input id="inputd1" type="text" name="Password" value="" size="30" maxlength="30"><br /><br />

         <input type="button" name="Only a button" value="Enter Site" id="Only a button" class="btn" onclick="pw(this.form)">
</form>
</div>

Interpretando el Script

En el formulario vemos que llama a la función «pw» y ésta a su vez llama a la función «getStyle«, bueno, pués es tan simple como poner un «alert();» dentro de la función «pw» para cazar la clave. Con éste método podemos cazar la clave del 90% de este tipo de pruebas.

29-08-2014 01-21-17alert

Con esto ya tenemos la clave. El usuario responde a la siguiente sentencia «d2==d1.length«, es decir, es el número de dígitos de la clave.

¿Fácil no?

Links

por ·Sin comentarios

Los retos criptográficos son muy variados y muchas veces la dificultad está en saber a que te enfrentas. En este caso pasa eso, te dan un código y si no has visto algo parecido en la vida, no sabes por donde empezar. El título del autor da una pequeña pista pero para los desconocedores no es suficiente. La pista es el título y dice «WTF?!?» y el código a descifrar es el siguiente:

[-]>[-]<
>+++++++++++[<+++++++++++>-]<.
>+++[<--->-]<-.
>++[<++>-]<++.
+.
>++++[<---->-]<-.
---.
+++.
.
>+++[<+++>-]<.
>+++[<--->-]<+.
>++++[<++++>-]<-.
>++++[<---->-]<--.
>+++[<+++>-]<-.
>++[<-->-]<--.
-.

Si eres una persona con recursos, realizaras varias búsquedas por la red y al final llegarás a la conclusión de que te enfrentas a BRAINFUCK, un lenguaje de programación esotérico como ya vimos en el reto de Root-Me.

Enlaces

por ·3 comentarios

Warning: This challenge is still active and therefore should not be resolved using this information.
Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.

Introducción

En los retos de esteganografía ya uno se espera de todo, y cuantos más haces más enrevesados encuentras. Hoy no, hoy vamos a tratar un clásico dentro de este tipo de retos, ocultar un archivo dentro de otro.

Buscando la solución

Prácticamente lo primero que hago cuando me descargo una imágen en éste tipo de retos es abrirla con un editor hexadecimal, y en este caso hemos dado en el clavo. La abrimos con un editor cualquiera y al final del archivo encontramos que estamos tratando con un archivo ZIP (cabecera PK).

29-08-2014 03-00-03

La abrimos con 7zip y vemos el prometido archivo txt, dentro ¿qué abrá?

29-08-2014-03-02-19

Links