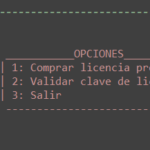
Hace unos años cuando empecé a trastear con Android y animado por mi afición a la Ingeniería Inversa, decidí realizar una serie de crackmes. Los dos primeros pasaron algo desapercibidos, pero el Crackme nº3 tuvo una gran repercusión en el mundillo y, aunque no fue el primer crackme para Android ni mucho menos, si que fue uno de los más estudiados. Todos ellos fueron publicados a través de crackmes.de y el nº3 en cuestión el 6 de Noviembre de 2010. Os dejo una lista de unas cuantas webs donde aparece analizado para que veáis la repercusión que a mi parecer tuvo.
Soluciones al crackme
- http://securityxploded.com/android_reversing.php
- http://www.spageek.net/deuruss-android-crackme03/
- https://github.com/spageek/solutions-to-crackmes/commits/master
- https://www.mgp25.com/androidCrackme03/
- http://www.techpluto.com/how-to-crack-games-on-android/
- http://docslide.us/documents/club-hack-mag-dec-2010.html
- http://www.symbianize.com/archive/index.php/t-678834.html
- http://feeds.feedburner.com/nyoret
- http://crackmes.de/users/deurus/android_crackme03/solutions/diff/browse
- Android Reverse Engineering – A Kick Start (Indian First Digital Security Magazine)
- http://www.programlife.net/android-crackme3.html
- http://www.codexiu.cn/android/blog/36058/
- http://blog.btrisk.com/2014/04/AndroidReverseTersineMuhendislikSmali.html