Intro
Hoy tenemos un crackme hecho en ensamblador y que cuenta con tres niveles. En el primero de todos nos enfrentamos a una «Splash screen» o nag. El segundo en un serial Hardcodeado y el tercero un número de serie asociado a un nombre.
Nopeando la Splash Screen
Abrimos el crackme con Olly y vamos a las «Intermodular Calls«, enseguida vemos la función que crea las ventanas «CreateWindowExA«. Se puede ver lo que parece ser la creación de la pantalla del crackme y al final hay algo que salta a la vista y es la propiedad «WS_TOPMOST», es decir, que se mantenga delante del resto de ventanas.
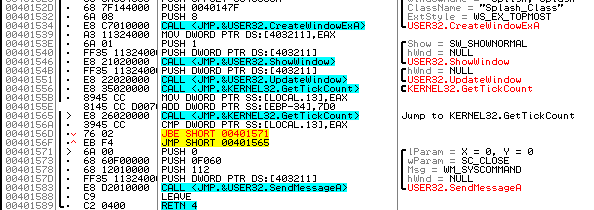
Pinchamos sobre la función y vamos a parar aquí.
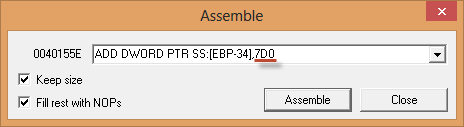
Vemos la llamada a CreateWindowExA que podríamos parchear pero vamos a pensar un poco. Vemos la función GetTickCount y que carga el valor 7D0. 7D0 es 2000 en decimal, que perfectamente pueden ser milisegundos, por lo tanto el parcheo más elegante sería poner la función GetTickCount a 0. En la imagen inferior se puede ver como queda parcheado el valor 7D0.
Probamos y funciona, pasamos a lo siguiente.
Serial Hardcodeado
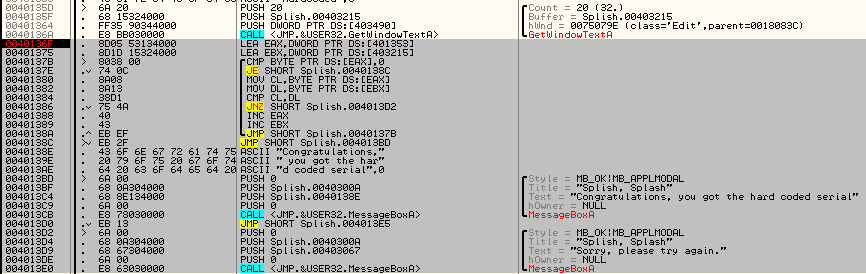
El mensaje de error del serial hardcodeado dice «Sorry, please try again». Lo buscamos en las string references y vamos a parar aquí.
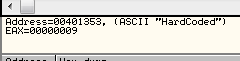
Vemos un bucle de comparación que carga unos bytes de la memoria, los bytes dicen «HardCoded«, probamos y prueba superada.
El nombre y número de serie
Con el mismo método de las string references localizamos el código que nos interesa. Metemos deurus como nombre y 12345 como serial y empezamos a tracear. Lo primero que hace es una serie de operaciones con nuestro nombre a las que podemos llamar aritmética modular. Aunque en la imagen viene bastante detallado se vé mejor con un ejemplo.
Ejemplo para Nombre: deurus
d e u r u s 64 65 75 72 75 73 -hex 100 101 117 114 117 115 -dec 1ºByte = ((Nombre[0] % 10)^0)+2 2ºByte = ((Nombre[1] % 10)^1)+2 3ºByte = ((Nombre[2] % 10)^2)+2 4ºByte = ((Nombre[3] % 10)^3)+2 5ºByte = ((Nombre[4] % 10)^4)+2 6ºByte = ((Nombre[5] % 10)^5)+2 1ºByte = ((100 Mod 10) Xor 0) + 2 2ºByte = ((101 Mod 10) Xor 1) + 2 3ºByte = ((117 Mod 10) Xor 2) + 2 4ºByte = ((114 Mod 10) Xor 3) + 2 5ºByte = ((117 Mod 10) Xor 4) + 2 6ºByte = ((115 Mod 10) Xor 5) + 2 Si el byte > 10 --> Byte = byte - 10 1ºByte = 2 2ºByte = 2 3ºByte = 7 4ºByte = 9 5ºByte = 5 6ºByte = 2
Lo que nos deja que los Bytes mágicos para deurus son: 227952.
Debido a la naturaleza de la operación IDIV y el bucle en general, llegamos a la conclusión de que para cada letra es un solo byte mágico y que este está comprendido entre 0 y 9.
A continuación realiza las siguientes operaciones con el serial introducido.
Ejemplo para serial: 12345
1 2 3 4 5 31 32 33 34 35 -hex 49 50 51 52 53 -dec 49 mod 10 = 9 50 mod 10 = 0 51 mod 10 = 1 52 mod 10 = 2 53 mod 10 = 3
Los bytes mágicos del serial son: 90123, que difieren bastante de los conseguidos con el nombre.
A continuación compara byte a byte 227952 con 90123.
En resumen, para cada nombre genera un código por cada letra y luego la comprobación del serial la realiza usando el módulo 10 del dígito ascii. Lo primero que se me ocurre es que necesitamos cotejar algún dígito del 0 al 9 para tener cubiertas todas las posibilidades. Realizamos manualmente mod 10 a los números del 0 al 9 y obtenemos sus valores.
(0) 48 mod 10 = 8 (1) 49 mod 10 = 9 (2) 50 mod 10 = 0 (3) 51 mod 10 = 1 (4) 52 mod 10 = 2 (5) 53 mod 10 = 3 (6) 54 mod 10 = 4 (7) 55 mod 10 = 5 (8) 56 mod 10 = 6 (9) 57 mod 10 = 7
Con esto ya podríamos generar un serial válido.
0123456789 - Nuestro alfabeto numérico 8901234567 - Su valor Mod 10
Por lo que para deurus un serial válido sería: 449174. Recordemos que los bytes mágicos para deurus eran «227952», solo hay que sustituir.
Para realizar un KeyGen más interesante, he sacado los valores de un alfabeto mayor y le he añadido una rutina aleatoria para que genere seriales diferentes para un mismo nombre.
'abcdefghijklmnñppqrstuvwxyz0123456789ABCDEFGHIJKLMNÑOPQRSTUVWXYZ - Alfabeto
'7890123456778901234567789018901234567567890123455678901234556880 - Valor
Dim suma As Integer = 0
'Para hacer el serial más divertido
Dim brute() As String = {"2", "3", "4", "5", "6", "7", "8", "9", "0", "1"}
Dim brute2() As String = {"d", "e", "f", "g", "h", "i", "j", "a", "b", "c"}
Dim brute3() As String = {"P", "Q", "R", "S", "T", "U", "j", "a", "D", "E"}
Dim alea As New Random()
txtserial.Text = ""
'Evito nombres mayores de 11 para evitar el BUG comentado en le manual
If Len(txtnombre.Text) > 0 And Len(txtnombre.Text) < 12 Then
For i = 1 To Len(txtnombre.Text)
Dim aleatorio As Integer = alea.Next(0, 9)
suma = (((Asc(Mid(txtnombre.Text, i, 1))) Mod 10) Xor i - 1) + 2
If suma > 9 Then
suma = suma - 10
End If
If (aleatorio) >= 0 And (aleatorio) <= 4 Then
txtserial.Text = txtserial.Text & brute(suma)
ElseIf (aleatorio) > 4 And (aleatorio) <= 7 Then
txtserial.Text = txtserial.Text & brute2(suma)
ElseIf (aleatorio) > 7 And (aleatorio) <= 10 Then
txtserial.Text = txtserial.Text & brute3(suma)
End If
suma = 0
Next
Else
txtserial.Text = "El Nombre..."
End If
Notas finales
Hay un pequeño bug en el almacenaje del nombre y serial y en el guardado de bytes mágicos del serial. Si nos fijamos en los bucles del nombre y el serial, vemos que los bytes mágicos del nombre los guarda a partir de la dirección de memoria 403258 y los bytes mágicos del serial a partir de 40324D. En la siguiente imagen podemos ver seleccionados los 11 primeros bytes donde se almacenan los bytes mágicos del serial. Vemos que hay seleccionados 11 bytes y que el siguiente sería ya 403258, precisamente donde están los bytes mágicos del nombre. Como puedes imaginar si escribes un serial >11 dígitos se solapan bytes y es una chapuza, de modo que el keygen lo he limitado a nombres de 11 dígitos.