• Introducción
• Funcionamiento de RSA
• OllyDbg
• Calculando un serial válido
• Ejemplo operacional
• Keygen
• Links

Introducción

Empezamos con lo que espero que sea una serie de crackmes RSA. En este caso en particular y como el propio autor nos adelanta, se trata de RSA-200.

En criptografía, RSA (Rivest, Shamir y Adleman) es un sistema criptográfico de clave pública desarrollado en 1977. Es el primer y más utilizado algoritmo de este tipo y es válido tanto para cifrar como para firmar digitalmente.

 Funcionamiento de RSA

1. Inicialmente es necesario generar aleatoriamente dos números primos grandes, a los que llamaremos p y q.
2. A continuación calcularemos n como producto de p y q:

   n = p * q

3. Se calcula fi:

   fi(n)=(p-1)(q-1)

4. Se calcula un número natural e de manera que MCD(e, fi(n))=1 , es decir e debe ser primo relativo de fi(n). Es lo mismo que buscar un numero impar por el que dividir fi(n) que de cero como resto.
5. Mediante el algoritmo extendido de Euclides se calcula d que es el inverso modular de e.

   Puede calcularse d=((Y*fi(n))+1)/e para Y=1,2,3,... hasta encontrar un d entero.

6. El par de números (e,n) son la clave pública.
7. El par de números (d,n) son la clave privada.
8. Cifrado: La función de cifrado es.

   c = m^e mod n

9. Descifrado: La función de descifrado es.

   m = c^d mod n

OllyDbg

Con OllyDbg analizamos la parte del código que nos interesa.

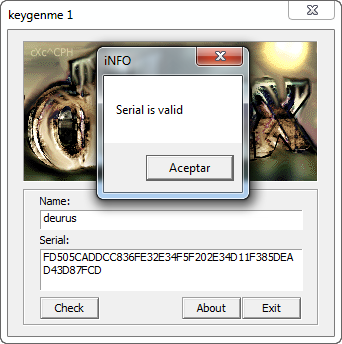
00401065  |>push    19                          ; /Count = 19 (25.)
00401067  |>push    00404330                    ; |Buffer = dihux_ke.00404330
0040106C  |>push    2711                        ; |ControlID = 2711 (10001.)
00401071  |>push    dword ptr [ebp+8]           ; |hWnd
00401074  |>call    <GetDlgItemTextA>           ; \GetDlgItemTextA
00401079  |>cmp     eax, 5                      ;  Tamaño nombre >= 5
0040107C  |>jb      00401214
00401082  |>cmp     eax, 14                     ;  Tamaño nombre <= 0x14
00401085  |>ja      00401214
0040108B  |>mov     [404429], eax
00401090  |>push    96                          ; /Count = 96 (150.)
00401095  |>push    00404349                    ; |Buffer = dihux_ke.00404349
0040109A  |>push    2712                        ; |ControlID = 2712 (10002.)
0040109F  |>push    dword ptr [ebp+8]           ; |hWnd
004010A2  |>call    <GetDlgItemTextA>           ; \GetDlgItemTextA
004010A7  |>test    al, al
........
004010D8  |>xor     ecx, ecx                    ;  Case 0 of switch 004010B6
004010DA  |>/push    0
004010DC  |>|call    <__BigCreate@4>
004010E1  |>|mov     [ecx*4+404411], eax
004010E8  |>|inc     ecx
004010E9  |>|cmp     ecx, 6
004010EC  |>\jnz     short 004010DA
004010EE  |>push    dword ptr [404411]          ; /Arg3 = 00B60000
004010F4  |>push    10                          ; |16??
004010F6  |>push    0040401F                    ; |Arg1 = 0040401F ASCII "8ACFB4D27CBC8C2024A30C9417BBCA41AF3FC3BD9BDFF97F89"
004010FB  |>call    <__BigIn@12>                ; \dihux_ke.004013F3
00401100  |>push    dword ptr [404415]          ; /Arg3 = 00C70000
00401106  |>push    10                          ; |Arg2 = 00000010
00401108  |>push    00404019                    ; |Arg1 = 00404019 ASCII "10001"
0040110D  |>call    <__BigIn@12>                ; \dihux_ke.004013F3
00401112  |>push    dword ptr [404425]          ; /Arg3 = 00CB0000
00401118  |>push    10                          ; |Arg2 = 00000010
0040111A  |>push    00404349                    ; |Arg1 = 00404349 ASCII "123456789123456789"
0040111F  |>call    <__BigIn@12>                ; \dihux_ke.004013F3
00401124  |>push    00404330                    ; /String = "deurus"
00401129  |>call    <lstrlenA>                  ; \lstrlenA
0040112E  |>push    dword ptr [404419]
00401134  |>push    eax
00401135  |>push    00404330                    ;  ASCII "deurus"
0040113A  |>call    <__BigInB256@12>
0040113F  |>push    dword ptr [404421]          ;  c
00401145  |>push    dword ptr [404411]          ;  n = 8ACFB4D27CBC8C2024A30C9417BBCA41AF3FC3BD9BDFF97F89
0040114B  |>push    dword ptr [404415]          ;  e = 10001
00401151  |>push    dword ptr [404425]          ;  serial
00401157  |>call    <__BigPowMod@16>            ;  c = serial^e (mod n)
0040115C  |>mov     eax, 1337
00401161  |>push    0                           ; /Arg4 = 00000000
00401163  |>push    dword ptr [40441D]          ; |x
00401169  |>push    eax                         ; |0x1337
0040116A  |>push    dword ptr [404421]          ; |c
00401170  |>call    <__BigDiv32@16>             ; \x = c/0x1337
00401175  |>push    dword ptr [40441D]          ;  x
0040117B  |>push    dword ptr [404419]          ;  nombre
00401181  |>call    <__BigCompare@8>            ; ¿x = nombre?
00401186  |>jnz     short 0040119C
00401188  |>push    0                           ; /Style = MB_OK|MB_APPLMODAL
0040118A  |>push    00404014                    ; |Title = "iNFO"
0040118F  |>push    00404004                    ; |Text = "Serial is valid"
00401194  |>push    dword ptr [ebp+8]           ; |hOwner
00401197  |>call    <MessageBoxA>               ; \MessageBoxA
0040119C  |>xor     ecx, ecx
0040119E  |>/push    dword ptr [ecx*4+404411]
004011A5  |>|call    <__BigDestroy@4>
004011AA  |>|inc     ecx
004011AB  |>|cmp     ecx, 6
004011AE  |>\jnz     short 0040119E

 Lo primero que observamos es que el código nos proporciona el exponente público (e) y el módulo (n).

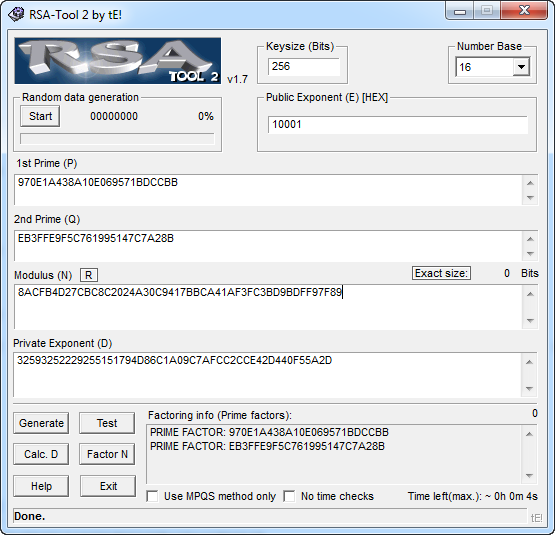
• e = 10001
• n = 8ACFB4D27CBC8C2024A30C9417BBCA41AF3FC3BD9BDFF97F89

A continuación halla c = serial^d mod n. Finalmente Divide c entre 0x1337 y lo compara con el nombre.

Como hemos visto en la teoría de RSA, necesitamos hallar el exponente privado (d) para poder desencriptar, según la fórmula vista anteriormente.

• Fórmula original: m=c^d mod n
• Nuestra fórmula: Serial = x^d mod n. Siendo x = c * 0x1337

Calculando un serial válido

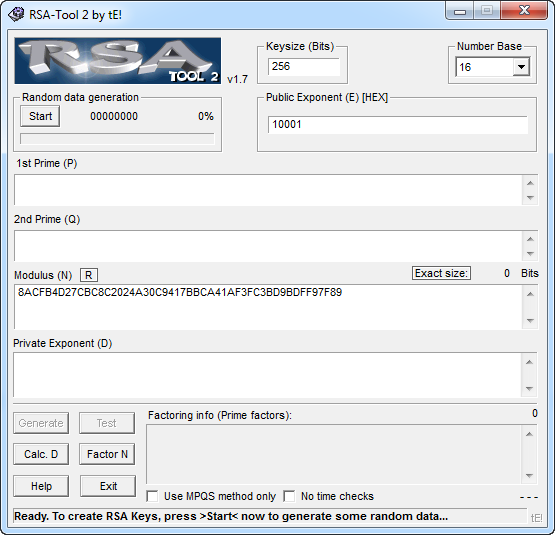
Existen varios ataques a RSA, nosotros vamos a usar el de factorización. Para ello vamos a usar la herramienta RSA Tool. Copiamos el módulo (n), el exponente público (e) y factorizamos (Factor N).

Hallados los primos p y q, hallamos d (Calc. D).

Una vez obtenido d solo nos queda obtener x, que recordemos es nombre * 0x1337.

Cuando decimos nombre nos referimos a los bytes del nombre en hexadecimal, para deurus serían 646575727573.

Ejemplo operacional

Nombre: deurus

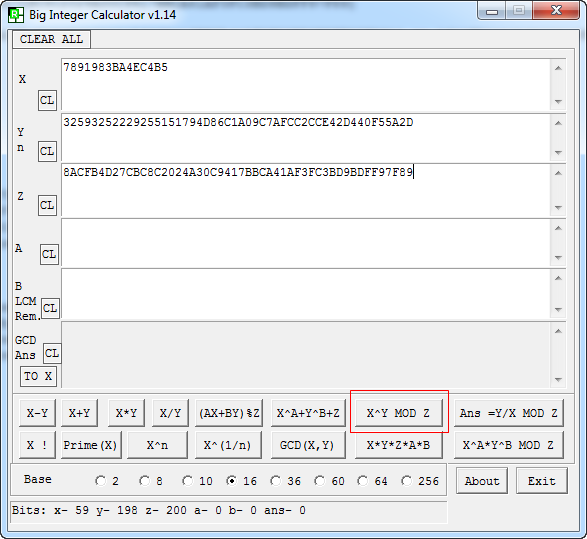
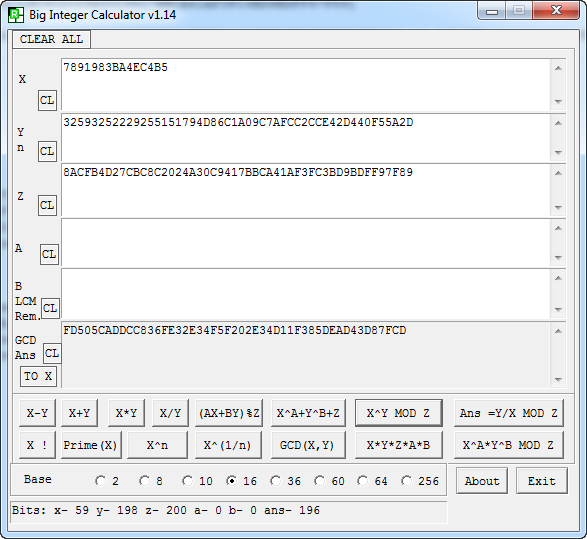
x = 646575727573 * 0x1337 = 7891983BA4EC4B5
Serial = x^d mod n
Serial = 7891983BA4EC4B5^32593252229255151794D86C1A09C7AFCC2CCE42D440F55A2D mod 8ACFB4D27CBC8C2024A30C9417BBCA41AF3FC3BD9BDFF97F89
Serial = FD505CADDCC836FE32E34F5F202E34D11F385DEAD43D87FCD

Como la calculadora de Windows se queda un poco corta para trabajar con números tan grandes, vamos a usar la herramienta Big Integer Calculator. A continuación os dejo unas imágenes del proceso.

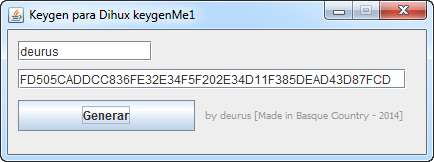
Keygen

En esta ocasión hemos elegido Java ya que permite trabajar con números grandes de forma sencilla, os dejo el código más importante.

JButton btnNewButton = new JButton("Generar");
btnNewButton.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent arg0) {
BigInteger serial = new BigInteger("0");
BigInteger n = new BigInteger("871332984042175151665553882265818310920539633758381377421193");//módulo
BigInteger d = new BigInteger("316042180198461106401603389463895139535543421270452849695277");//exponente privado
BigInteger x = new BigInteger("4919");//0x1337
String nombre = t1.getText();
BigInteger nombre2 = new BigInteger(nombre.getBytes());
nombre2 = nombre2.multiply(x);
serial = nombre2.modPow(d, n);
t2.setText(serial.toString(16).toUpperCase());
}
});

Links

• RSA (wikipedia)
• El algoritmo RSA y la factorización de números grandes (recomendable)
• Exponenciación modular (wikipedia)
• RSA Tool
• Big Integer Calculator v1.14
• Crackme
• Keygen

Blooper Tech Movie VI - Dexter 1x08 (S01E08)

Hace poco me puse a leer El oscuro pasajero de Jeff Lindsay, novela que inspiró la serie Dexter. La nostalgia

Descargar contenido multimedia de ciertas webs

Hoy en día, la descarga de contenido multimedia de ciertas webs es imposible o muy difícil. En ciertos casos lo

WinFan's NETCrackMe#1 Keygen

Introducción Tal y como nos adelanta el creador está programado en .NET. Lo abrimos para ver su comportamiento y a

Entrevista a Karpoff de "Karpoff Spanish Tutor"

Karpoff.es Hace unos días intenté contactar con Karpoff ya que fué una inspiración para mi y muchos otros, lo conseguí

1 2 3 … 28 Next »