CoSH’s Crackme 3 KeyGen

por ·Sin comentarios

Intro

Hoy tenemos un crackme realizado en Visual C++ 6. Es el típico serial asociado a un nombre.

El algoritmo

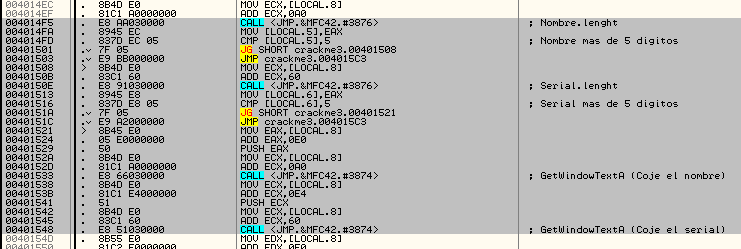
Localizamos con Olly la rutina de comprobación del serial y empezamos a analizar. Vemos una serie de Calls que lo único que hacen es comprobar el tamaño de nuestro nombre y serial y si es <5 dígitos nos tira afuera.

saltos_iniciales

Una vez pasada la traba anterior procede con un bucle para el nombre y otro para el serial. Yo he metido deurus y 123456. El bucle del nombre hace xor al los dígitos ascii con un valor incremental a partir de 1. Reconvierte el valor resultante en su caracter correspondiente y lo almacena.

00401576     |.  B9 01000000   MOV ECX,1                         ; ECX = 1
0040157B     |.  33D2          XOR EDX,EDX
0040157D     |.  8B45 E4       MOV EAX,[LOCAL.7]                 ; EAX = Nombre
00401580     |>  8A18          /MOV BL,BYTE PTR DS:[EAX]         ; BL = digito que toque  <--
00401582     |.  32D9          |XOR BL,CL                        ; digito XOR ECX
00401584     |.  8818          |MOV BYTE PTR DS:[EAX],BL         ; sustituye el digito nombre por el resultante del xor
00401586     |.  41            |INC ECX                          ; ECX++
00401587     |.  40            |INC EAX                          ; Siguiente digito
00401588     |.  8038 00       |CMP BYTE PTR DS:[EAX],0
0040158B     |.^ 75 F3         \JNZ SHORT crackme3.00401580      ; Bucle -->

 Ejemplo:

d  e  u  r  u  s
64 65 75 72 75 73

(d)64 xor 1 = 65(e)
(e)65 xor 2 = 67(g)
(u)75 xor 3 = 76(v)
(r)72 xor 4 = 76(v)
(u)75 xor 5 = 70(p)
(s)73 xor 6 = 75(u)

Nombre:    deurus
Resultado: egvvpu

Hace lo mismo con el serial pero con el valor incremental a partir de 0xA (10).

00401593     |.  B9 0A000000    MOV ECX,0A                      ; ECX = A
00401598     |.  33D2           XOR EDX,EDX
0040159A     |.  8B45 F0        MOV EAX,[LOCAL.4]               ; EAX = Serial
0040159D     |>  8A18           /MOV BL,BYTE PTR DS:[EAX]       ; BL = digito que toque  <--
0040159F     |.  32D9           |XOR BL,CL                      ; BL XOR CL
004015A1     |.  8818           |MOV BYTE PTR DS:[EAX],BL       ; sustituye el digito serial por el resultante del xor
004015A3     |.  41             |INC ECX                        ; ECX++
004015A4     |.  40             |INC EAX                        ; Siguiente digito
004015A5     |.  8038 00        |CMP BYTE PTR DS:[EAX],0
004015A8     |.^ 75 F3          \JNZ SHORT crackme3.0040159D    ; Bucle -->

Ejemplo:

1  2  3  4  5  6
31 32 33 34 35 35

(1)31 xor A = 3B(;)
(2)32 xor B = 39(9)
(3)33 xor C = 3F(?)
(4)34 xor D = 39(9)
(5)35 xor E = 3B(;)
(6)36 xor F = 39(9)

Serial:    123456
Resultado: ;9?9;9

A continuación compara «egvvpu» con «;9?9;9» byte a byte.

KeyGen

El KeyGen quedaría así

for(int i = 0; i <= strlen(Nombre); i = i + 1)
                {
                        Serial[i] = (Nombre[i]^(i+1))^(0xA + i);
                }

 Links

Revisión al Software de Innotechnix
Habitualmente suelo descargar shareware por diversión para evaluar de que manera protegen los programadores su software. Cada vez es más
LaFarge's Crackme 2 - Keygen por Injerto
Intro Hoy vamos a hacer algo diferente, vamos a hacer un keygen con la propia víctima. El término anglosajón para
Keygen para el CrackMe Pythagoras de Spider
Introducción Hoy tenemos aquí un bonito crackme matemático realizado por Spider. El crackme está realizado en ensamblador y precisamente por
Andy's Keygenme Keygen (AutoIt)
Introducción  Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro

LaFarge’s Crackme 2 – Keygen por Injerto

por ·Sin comentarios

Intro

Hoy vamos a hacer algo diferente, vamos a hacer un keygen con la propia víctima. El término anglosajón para esto es «selfkeygening» y no es que esté muy bien visto por los reversers pero a veces nos puede sacar de apuros.

La víctima elegida es el Crackme 2 de LaFarge. Está hecho en ensamblador.

Injerto Light

Primeramente vamos a realizar un injerto light, con esto quiero decir que vamos a mostrar el serial bueno en la MessageBox de error.

Abrimos Olly y localizamos el código de comprobación del serial, tenemos suerte ya que el serial se muestra completamente y no se comprueba byte a byte ni cosas raras. En la imagen inferior os muestro el serial bueno para el nombre deurus y el mensaje de error. Como podeis observar el serial bueno se saca de memoria con la instrucción PUSH 406749 y el mensaje de error con PUSH 406306.

parche01

Si cambiamos el PUSH del serial por el de el mensaje de error ya lo tendriámos. Nos situamos encima del PUSH 406306 y pulsamos espacio, nos saldrá un diálogo con el push, lo modificamos y le damos a Assemble.

10-09-2014 20-37-18

Ahora el crackme cada vez que le demos a Check it! nos mostrará:

nagserial

Keygen a partir de la víctima

Pero no nos vamos a quedar ahí. Lo interesante sería que el serial bueno lo mostrara en la caja de texto del serial. Esto lo vamos a hacer con la función user32.SetDlgItemTextA.

setdlgitemtext

Según dice la función necesitamos el handle de la ventana, el ID de la caja de texto y el string a mostrar. La primera y segunda la obtenemos fijándonos en la función GetDlgItemTextA que recoje el serial introducido por nosotros. La string es el PUSH 406749.

handleandid

Con esto ya tenemos todo lo que necesitamos excepto el espacio dentro del código, en este caso lo lógico es parchear las MessageBox de error y acierto. Las seleccionamos, click derecho y Edit > Fill with NOPs.

10-09-2014 20-39-24

nopeamos

Ahora escribimos el injerto.

injertokeygen

Finalmente con Resource Hack cambiamos el aspecto del programa para que quede más profesional y listo. Tenemos pendiente hacer el keygen puro y duro, venga agur.

10-09-2014 21-04-52

Links

Cruehead’s Crackme 2.0 Serial [2/3]
Introducción Continuamos con la segunda entrega de Cruehead. En este caso nos encontramos con un único campo de contraseña para
CanYouHack.it Crack6 Challenge - Lights Out (English)
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en
Blooper Tech Movie IV – La Jungla 4.0 (Live Free or Die Hard)
La esperada cuarta entrega de La Jungla de Cristal se metió de lleno en el mundo de los Hackers. Cuando
Stego XVI - Bytes
Intro Os comparto un reto stego que me gustó cuando lo hice hace unos años. En realidad se tarda pocos

lost_in_bin

por ·Sin comentarios

Estamos ante un ELF un poco más interesante que los vistos anteriormente. Básicamente porque es divertido y fácil encontrar la solución en el decompilado y quizá por evocar recuerdos de tiempos pretéritos.

ELF Decompilado

/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
   Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>

   Detected compiler: GNU C++
*/

#include <defs.h>


//-------------------------------------------------------------------------
// Function declarations

__int64 (**init_proc())(void);
__int64 sub_400650(); // weak
// int printf(const char *format, ...);
// int puts(const char *s);
// void __noreturn exit(int status);
// size_t strlen(const char *s);
// __int64 __fastcall MD5(_QWORD, _QWORD, _QWORD); weak
// int sprintf(char *s, const char *format, ...);
// __int64 ptrace(enum __ptrace_request request, ...);
// __int64 strtol(const char *nptr, char **endptr, int base);
// __int64 __isoc99_scanf(const char *, ...); weak
// int memcmp(const void *s1, const void *s2, size_t n);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
void *sub_400730();
__int64 sub_400760();
void *sub_4007A0();
__int64 sub_4007D0();
void fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// __int64 _gmon_start__(void); weak

//-------------------------------------------------------------------------
// Data declarations

_UNKNOWN main;
_UNKNOWN init;
__int64 (__fastcall *funcs_400E29)() = &sub_4007D0; // weak
__int64 (__fastcall *off_601DF8)() = &sub_4007A0; // weak
__int64 (*qword_602010)(void) = NULL; // weak
char *off_602080 = "FLAG-%s\n"; // idb
char a7yq2hryrn5yJga[16] = "7Yq2hrYRn5Y`jga"; // weak
const char aO6uH[] = "(O6U,H\""; // idb
_UNKNOWN unk_6020B8; // weak
_UNKNOWN unk_6020C8; // weak
char byte_6020E0; // weak
char s1; // idb
char byte_602110[]; // weak
char byte_602120[33]; // weak
char byte_602141[7]; // idb
__int64 qword_602148; // weak
__int64 qword_602150; // weak
__int64 qword_602158; // weak
__int64 qword_602160; // weak
__int64 qword_602178; // weak


//----- (0000000000400630) ----------------------------------------------------
__int64 (**init_proc())(void)
{
  __int64 (**result)(void); // rax

  result = &_gmon_start__;
  if ( &_gmon_start__ )
    return (__int64 (**)(void))_gmon_start__();
  return result;
}
// 6021D8: using guessed type __int64 _gmon_start__(void);

//----- (0000000000400650) ----------------------------------------------------
__int64 sub_400650()
{
  return qword_602010();
}
// 400650: using guessed type __int64 sub_400650();
// 602010: using guessed type __int64 (*qword_602010)(void);

//----- (0000000000400700) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
  __int64 v3; // rax
  int v4; // esi
  __int64 v5; // [rsp-8h] [rbp-8h] BYREF
  char *retaddr; // [rsp+0h] [rbp+0h] BYREF

  v4 = v5;
  v5 = v3;
  _libc_start_main((int (__fastcall *)(int, char **, char **))main, v4, &retaddr, (void (*)(void))init, fini, a3, &v5);
  __halt();
}
// 400706: positive sp value 8 has been found
// 40070D: variable 'v3' is possibly undefined

//----- (0000000000400730) ----------------------------------------------------
void *sub_400730()
{
  return &unk_6020C8;
}

//----- (0000000000400760) ----------------------------------------------------
__int64 sub_400760()
{
  return 0LL;
}

//----- (00000000004007A0) ----------------------------------------------------
void *sub_4007A0()
{
  void *result; // rax

  if ( !byte_6020E0 )
  {
    result = sub_400730();
    byte_6020E0 = 1;
  }
  return result;
}
// 6020E0: using guessed type char byte_6020E0;

//----- (00000000004007D0) ----------------------------------------------------
__int64 sub_4007D0()
{
  return sub_400760();
}

//----- (00000000004007D7) ----------------------------------------------------
__int64 __fastcall main(int a1, char **a2, char **a3)
{
  size_t v3; // rax
  size_t v4; // rax
  int i; // [rsp+1Ch] [rbp-24h]
  int n; // [rsp+20h] [rbp-20h]
  int m; // [rsp+24h] [rbp-1Ch]
  int k; // [rsp+28h] [rbp-18h]
  int j; // [rsp+2Ch] [rbp-14h]

  if ( ptrace(PTRACE_TRACEME, 0LL, 0LL, 0LL) == -1 )
    goto LABEL_2;
  if ( a1 > 4 )
  {
    qword_602148 = strtol(a2[1], 0LL, 10);
    if ( qword_602148 )
    {
      qword_602150 = strtol(a2[2], 0LL, 10);
      if ( qword_602150 )
      {
        qword_602158 = strtol(a2[3], 0LL, 10);
        if ( qword_602158 )
        {
          qword_602160 = strtol(a2[4], 0LL, 10);
          if ( qword_602160 )
          {
            if ( -24 * qword_602148 - 18 * qword_602150 - 15 * qword_602158 - 12 * qword_602160 == -18393
              && 9 * qword_602158 + 18 * (qword_602150 + qword_602148) - 9 * qword_602160 == 4419
              && 4 * qword_602158 + 16 * qword_602148 + 12 * qword_602150 + 2 * qword_602160 == 7300
              && -6 * (qword_602150 + qword_602148) - 3 * qword_602158 - 11 * qword_602160 == -8613 )
            {
              qword_602178 = qword_602158 + qword_602150 * qword_602148 - qword_602160;
              sprintf(byte_602141, "%06x", qword_602178);
              v4 = strlen(byte_602141);
              MD5(byte_602141, v4, byte_602110);
              for ( i = 0; i <= 15; ++i )
                sprintf(&byte_602120[2 * i], "%02x", (unsigned __int8)byte_602110[i]);
              printf(off_602080, byte_602120);
              exit(0);
            }
          }
        }
      }
    }
LABEL_2:
    printf("password : ");
    __isoc99_scanf("%s", &s1);
    if ( strlen(&s1) > 0x10 )
    {
      puts("the password must be less than 16 character");
      exit(1);
    }
    for ( j = 0; j < strlen(&s1); ++j )
      *(&s1 + j) ^= 6u;
    if ( !strcmp(&s1, a7yq2hryrn5yJga) )
    {
      v3 = strlen(&s1);
      MD5(&s1, v3, byte_602110);
      for ( k = 0; k <= 15; ++k )
        sprintf(&byte_602120[2 * k], "%02x", (unsigned __int8)byte_602110[k]);
      printf(off_602080, byte_602120);
      exit(0);
    }
    puts("bad password!");
    exit(0);
  }
  printf("password : ");
  __isoc99_scanf("%s", &s1);
  if ( strlen(&s1) > 0x10 )
  {
    puts("the password must be less than 16 character");
    exit(1);
  }
  for ( m = 0; m < strlen(&s1); ++m )
  {
    *(&s1 + m) ^= 2u;
    ++*(&s1 + m);
    *(&s1 + m) = ~*(&s1 + m);
  }
  if ( !memcmp(&s1, &unk_6020B8, 9uLL) )
  {
    for ( n = 0; n < strlen(aO6uH); n += 2 )
    {
      aO6uH[n] ^= 0x45u;
      aO6uH[n + 1] ^= 0x26u;
    }
    puts(aO6uH);
  }
  else
  {
    puts("bad password!");
  }
  return 0LL;
}
// 4006A0: using guessed type __int64 __fastcall MD5(_QWORD, _QWORD, _QWORD);
// 4006E0: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 602148: using guessed type __int64 qword_602148;
// 602150: using guessed type __int64 qword_602150;
// 602158: using guessed type __int64 qword_602158;
// 602160: using guessed type __int64 qword_602160;
// 602178: using guessed type __int64 qword_602178;

//----- (0000000000400DE0) ----------------------------------------------------
void __fastcall init(unsigned int a1, __int64 a2, __int64 a3)
{
  signed __int64 v3; // rbp
  __int64 i; // rbx

  v3 = &off_601DF8 - &funcs_400E29;
  init_proc();
  if ( v3 )
  {
    for ( i = 0LL; i != v3; ++i )
      (*(&funcs_400E29 + i))();
  }
}
// 601DF0: using guessed type __int64 (__fastcall *funcs_400E29)();
// 601DF8: using guessed type __int64 (__fastcall *off_601DF8)();

//----- (0000000000400E54) ----------------------------------------------------
void term_proc()
{
  ;
}

// nfuncs=33 queued=10 decompiled=10 lumina nreq=0 worse=0 better=0
// ALL OK, 10 function(s) have been successfully decompiled

Análisis estático

Anti-debug

Si la función ptrace retorna -1, significa que el programa está siendo depurado y redirige a LABEL_2.

if (ptrace(PTRACE_TRACEME, 0LL, 0LL, 0LL) == -1) {
    goto LABEL_2;
}

Cálculos y validaciones

El programa espera al menos 5 argumentos (nombre del programa y cuatro números enteros). Si se proporcionan los cuatro números enteros, se realizan los siguientes cálculos:

if (-24 * qword_602148 - 18 * qword_602150 - 15 * qword_602158 - 12 * qword_602160 == -18393
    && 9 * qword_602158 + 18 * (qword_602150 + qword_602148) - 9 * qword_602160 == 4419
    && 4 * qword_602158 + 16 * qword_602148 + 12 * qword_602150 + 2 * qword_602160 == 7300
    && -6 * (qword_602150 + qword_602148) - 3 * qword_602158 - 11 * qword_602160 == -8613)

Esto es un sistema de ecuaciones lineales mondo y lirondo que debe ser resuelto para encontrar los valores correctos de qword_602148, qword_602150, qword_602158 y qword_602160. Una vez resuelto el sistema de ecuaciones se realiza la operación:

 qword_602178 = qword_602158 + qword_602150 * qword_602148 - qword_602160;

A continuación se pasa el resultado de la variable qword_602178 a hexadecimal y se genera su hash MD5.

Solución en Python

Lo más rápido en esta ocasión es usar Python, pero esto se puede resolver hasta con lápiz y papel 😉

from sympy import symbols, Eq, solve
import hashlib

# Definir las variables
A, B, C, D = symbols('A B C D')

# Definir las ecuaciones
eq1 = Eq(-24*A - 18*B - 15*C - 12*D, -18393)
eq2 = Eq(9*C + 18*(A + B) - 9*D, 4419)
eq3 = Eq(4*C + 16*A + 12*B + 2*D, 7300)
eq4 = Eq(-6*(A + B) - 3*C - 11*D, -8613)

# Resolver el sistema de ecuaciones
solution = solve((eq1, eq2, eq3, eq4), (A, B, C, D))

# Verificar si se encontró una solución
if solution:
    print("Solución encontrada:")
    print(solution)

    # Obtener los valores de A, B, C y D
    A_val = solution[A]
    B_val = solution[B]
    C_val = solution[C]
    D_val = solution[D]

    # Mostrar los valores encontrados
    print(f"A = {A_val}")
    print(f"B = {B_val}")
    print(f"C = {C_val}")
    print(f"D = {D_val}")

    # Calcular qword_602178
    qword_602178 = C_val + B_val * A_val - D_val
    qword_602178 = int(qword_602178)  # Convertir a entero de Python
    print(f"qword_602178 = {qword_602178}")

    # Convertir qword_602178 a una cadena en formato hexadecimal
    byte_602141 = f"{qword_602178:06x}"
    print(f"byte_602141 (hex) = {byte_602141}")

    # Calcular el MD5 de la cadena
    md5_hash = hashlib.md5(byte_602141.encode()).hexdigest()
    print(f"MD5 hash = {md5_hash}")

    # Generar la flag
    flag = f"FLAG-{md5_hash}"
    print(f"Flag = {flag}")

else:
    print("No se encontró una solución.")

Al ejecutar el script veremos algo como esto:

Solución encontrada:
{A: 227, B: 115, C: 317, D: 510}
A = 227
B = 115
C = 317
D = 510
qword_602178 = 25912
byte_602141 (hex) = 006538
MD5 hash = 21a84f2c7c7fd432edf1686215db....
Flag = FLAG-21a84f2c7c7fd432edf1686215db....

CanYouHack.it Crack6 Challenge – Lights Out (English)

por ·Sin comentarios

Warning: This challenge is still active and therefore should not be resolved using this information.
Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.

Intro

This crackme is for the crack challenge 6 of canyouhack.it.

In this crackme the goal is to turn on all the lights. Note that a light off to the next, so if we interrupt this, we win.

Tools

Exeinfo (For crackme info)

Delphi Decompiler (For decompile)

 OllyDbg (For debug)

Decompiling

With Delphi Decompiler we can found easy the buttons and his offsets.
Go to the offset 401A64 in OllyDbg and analyze the code.
We view two jumps, one turn ON the light and the other Turn OFF the next light. Patching the call from offset 401A8B we get the serial.

Links

VideoTutorial - KeyGen para el Crackme#1 de WinFan
http://youtu.be/b9-GdmIQINQ Lista de reproducción
AfKayAs's CrackMe#2 KeyGen
Intro Hoy vamos a desmitificar un poco a Visual Basic. El Crackme reza que acabemos con la nag y hagamos
Blooper Tech Movie I - The Ring (La Señal)
Con The Ring inauguro una nueva sección llamada Blooper Tech Movie (BTM), algo así como pifias o tomas falsas tecnológicas
Shadow's Register Me - Parchear un .Net
Introducción Este es un crackme hecho en .Net con dos Nags a parchear y un algoritmo muy sencillo pero que

AfKayAs’s CrackMe#2 KeyGen

por ·Sin comentarios

Intro

Hoy vamos a desmitificar un poco a Visual Basic. El Crackme reza que acabemos con la nag y hagamos un keygen.

La NAG

formnag

Lo primero que debemos establecer es a que tipo de Nag nos estamos enfrentando, si es una MessageBox, se localiza y se parchea, si es un formulario la cosa ya cambia un poco, ya que encontrar esa parte del código puede resultar tedioso.

Yo voy a utilizar el camino fácil. En VB contamos con una estupenda herramienta como es VBReformer, que nos muestra las entrañas del crackme y nos posibilita cambiar ciertos parametros.

Abrimos el crackme con VBReformer y vemos su contenido. Localizamos rápidamente el formulario que aparece inicialmente (CMSplash) y el temporizador que contiene (Timer1). Inicialmente el timer tiene un interval de 7000, es decir, la nag se muestra durante 7 segundos. Es tan sencillo como cambiarlo por 1 y guardar el ejecutable (File > Save binary as).

parcheform

Si no disponemos de esta estupenda herramienta, siempre podemos localizar el timer con un editor hexadecimal. Localizamos en Olly el nombre del timer (en las string references lo veréis), y lo buscamos en el editor hexadecimal. La duración de la nag la debemos estimar nosotros y a continuación buscar ese valor hexadecimal. Imaginemos que estimamos que son 7 segundos, lo pasamos a milisegundos y a hexadecimal. 7000 = 0x1B58. Buscamos en el editor hexadecimal «Timer1» y a continuación localizamos el valor 1B58 invertido, es decir, 581B. En las imágenes inferiores se ve claro.

hextimer1original

hextimer1parcheado

Cambiando el valor ya lo tendriámos.

El algoritmo

El algoritmo de este crackme es muy sencillo pero he elegido este en concreto para que veáis las vueltas que da VB para hacer 6 operaciones matemáticas. A continuación tenéis el código íntegro comentado y debajo el resumen.

004081F5      .  FF15 F8B04000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaLenBstr>]    ;  MSVBVM50.__vbaLenBstr
004081FB      .  8BF8                     MOV EDI,EAX
004081FD      .  8B4D E8                  MOV ECX,DWORD PTR SS:[EBP-18]
00408200      .  69FF 385B0100            IMUL EDI,EDI,15B38                              ;  TEMP = Len(nombre) *15B38
00408206      .  51                       PUSH ECX
00408207      .  0F80 B7050000            JO CrackmeV.004087C4
0040820D      .  FF15 0CB14000            CALL DWORD PTR DS:[<&MSVBVM50.#516>]            ;  MSVBVM50.rtcAnsiValueBstr
00408213      .  0FBFD0                   MOVSX EDX,AX                                    ;  digito a ax
00408216      .  03FA                     ADD EDI,EDX                                     ;  TEMP +=1digito
00408218      .  0F80 A6050000            JO CrackmeV.004087C4
0040821E      .  57                       PUSH EDI                                        ;  MSVBVM50.__vbaObjSet
0040821F      .  FF15 F4B04000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrI4>]      ;  MSVBVM50.__vbaStrI4
00408225      .  8BD0                     MOV EDX,EAX
00408227      .  8D4D E0                  LEA ECX,DWORD PTR SS:[EBP-20]
0040822A      .  FF15 94B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrMove>]    ;  MSVBVM50.__vbaStrMove
00408230      .  8BBD 50FFFFFF            MOV EDI,DWORD PTR SS:[EBP-B0]
00408236      .  50                       PUSH EAX
00408237      .  57                       PUSH EDI                                        ;  MSVBVM50.__vbaObjSet
00408238      .  FF93 A4000000            CALL DWORD PTR DS:[EBX+A4]                      ;  MSVBVM50.0F050D32
0040823E      .  85C0                     TEST EAX,EAX
00408240      .  7D 12                    JGE SHORT CrackmeV.00408254
00408242      .  68 A4000000              PUSH 0A4
00408247      .  68 AC6F4000              PUSH CrackmeV.00406FAC
0040824C      .  57                       PUSH EDI                                        ;  MSVBVM50.__vbaObjSet
0040824D      .  50                       PUSH EAX
0040824E      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
00408254      >  8D45 E0                  LEA EAX,DWORD PTR SS:[EBP-20]
00408257      .  8D4D E4                  LEA ECX,DWORD PTR SS:[EBP-1C]
0040825A      .  50                       PUSH EAX
0040825B      .  8D55 E8                  LEA EDX,DWORD PTR SS:[EBP-18]
0040825E      .  51                       PUSH ECX
0040825F      .  52                       PUSH EDX
00408260      .  6A 03                    PUSH 3
00408262      .  FF15 80B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeStrList>>;  MSVBVM50.__vbaFreeStrList
00408268      .  83C4 10                  ADD ESP,10
0040826B      .  8D45 D4                  LEA EAX,DWORD PTR SS:[EBP-2C]
0040826E      .  8D4D D8                  LEA ECX,DWORD PTR SS:[EBP-28]
00408271      .  8D55 DC                  LEA EDX,DWORD PTR SS:[EBP-24]
00408274      .  50                       PUSH EAX
00408275      .  51                       PUSH ECX
00408276      .  52                       PUSH EDX
00408277      .  6A 03                    PUSH 3
00408279      .  FF15 08B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeObjList>>;  MSVBVM50.__vbaFreeObjList
0040827F      .  8B9D 40FFFFFF            MOV EBX,DWORD PTR SS:[EBP-C0]                   ;  CrackmeV.00409A68
00408285      .  83C4 10                  ADD ESP,10
00408288      .  8B83 FC020000            MOV EAX,DWORD PTR DS:[EBX+2FC]
0040828E      .  56                       PUSH ESI
0040828F      .  8985 38FFFFFF            MOV DWORD PTR SS:[EBP-C8],EAX
00408295      .  FFD0                     CALL EAX
00408297      .  8B3D 20B14000            MOV EDI,DWORD PTR DS:[<&MSVBVM50.__vbaObjSet>]  ;  MSVBVM50.__vbaObjSet
0040829D      .  50                       PUSH EAX
0040829E      .  8D45 D8                  LEA EAX,DWORD PTR SS:[EBP-28]
004082A1      .  50                       PUSH EAX
004082A2      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet; <&MSVBVM50.__vbaObjSet>
004082A4      .  56                       PUSH ESI
004082A5      .  8985 58FFFFFF            MOV DWORD PTR SS:[EBP-A8],EAX
004082AB      .  FF93 08030000            CALL DWORD PTR DS:[EBX+308]
004082B1      .  8D4D DC                  LEA ECX,DWORD PTR SS:[EBP-24]
004082B4      .  50                       PUSH EAX
004082B5      .  51                       PUSH ECX
004082B6      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet
004082B8      .  8BD8                     MOV EBX,EAX
004082BA      .  8D45 E8                  LEA EAX,DWORD PTR SS:[EBP-18]
004082BD      .  50                       PUSH EAX
004082BE      .  53                       PUSH EBX
004082BF      .  8B13                     MOV EDX,DWORD PTR DS:[EBX]                      ;  MSVBVM50.0F025A95
004082C1      .  FF92 A0000000            CALL DWORD PTR DS:[EDX+A0]
004082C7      .  85C0                     TEST EAX,EAX
004082C9      .  7D 12                    JGE SHORT CrackmeV.004082DD
004082CB      .  68 A0000000              PUSH 0A0
004082D0      .  68 AC6F4000              PUSH CrackmeV.00406FAC
004082D5      .  53                       PUSH EBX
004082D6      .  50                       PUSH EAX
004082D7      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
004082DD      >  8B8D 58FFFFFF            MOV ECX,DWORD PTR SS:[EBP-A8]
004082E3      .  8B55 E8                  MOV EDX,DWORD PTR SS:[EBP-18]
004082E6      .  52                       PUSH EDX
004082E7      .  8B19                     MOV EBX,DWORD PTR DS:[ECX]
004082E9      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004082EF      .  D905 08104000            FLD DWORD PTR DS:[401008]
004082F5      .  833D 00904000 00         CMP DWORD PTR DS:[409000],0
004082FC      .  75 08                    JNZ SHORT CrackmeV.00408306
004082FE      .  D835 0C104000            FDIV DWORD PTR DS:[40100C]                      ;  10 / 5 = 2
00408304      .  EB 0B                    JMP SHORT CrackmeV.00408311
00408306      >  FF35 0C104000            PUSH DWORD PTR DS:[40100C]
0040830C      .  E8 578DFFFF              CALL <JMP.&MSVBVM50._adj_fdiv_m32>
00408311      >  83EC 08                  SUB ESP,8
00408314      .  DFE0                     FSTSW AX
00408316      .  A8 0D                    TEST AL,0D
00408318      .  0F85 A1040000            JNZ CrackmeV.004087BF
0040831E      .  DEC1                     FADDP ST(1),ST                                  ;  TEMP +=2
00408320      .  DFE0                     FSTSW AX
00408322      .  A8 0D                    TEST AL,0D
00408324      .  0F85 95040000            JNZ CrackmeV.004087BF
0040832A      .  DD1C24                   FSTP QWORD PTR SS:[ESP]
0040832D      .  FF15 48B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrR8>]      ;  MSVBVM50.__vbaStrR8
00408333      .  8BD0                     MOV EDX,EAX
00408335      .  8D4D E4                  LEA ECX,DWORD PTR SS:[EBP-1C]
00408338      .  FF15 94B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrMove>]    ;  MSVBVM50.__vbaStrMove
0040833E      .  899D 34FFFFFF            MOV DWORD PTR SS:[EBP-CC],EBX
00408344      .  8B9D 58FFFFFF            MOV EBX,DWORD PTR SS:[EBP-A8]
0040834A      .  50                       PUSH EAX
0040834B      .  8B85 34FFFFFF            MOV EAX,DWORD PTR SS:[EBP-CC]
00408351      .  53                       PUSH EBX
00408352      .  FF90 A4000000            CALL DWORD PTR DS:[EAX+A4]
00408358      .  85C0                     TEST EAX,EAX
0040835A      .  7D 12                    JGE SHORT CrackmeV.0040836E
0040835C      .  68 A4000000              PUSH 0A4
00408361      .  68 AC6F4000              PUSH CrackmeV.00406FAC
00408366      .  53                       PUSH EBX
00408367      .  50                       PUSH EAX
00408368      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
0040836E      >  8D4D E4                  LEA ECX,DWORD PTR SS:[EBP-1C]
00408371      .  8D55 E8                  LEA EDX,DWORD PTR SS:[EBP-18]
00408374      .  51                       PUSH ECX
00408375      .  52                       PUSH EDX
00408376      .  6A 02                    PUSH 2
00408378      .  FF15 80B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeStrList>>;  MSVBVM50.__vbaFreeStrList
0040837E      .  83C4 0C                  ADD ESP,0C
00408381      .  8D45 D8                  LEA EAX,DWORD PTR SS:[EBP-28]
00408384      .  8D4D DC                  LEA ECX,DWORD PTR SS:[EBP-24]
00408387      .  50                       PUSH EAX
00408388      .  51                       PUSH ECX
00408389      .  6A 02                    PUSH 2
0040838B      .  FF15 08B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeObjList>>;  MSVBVM50.__vbaFreeObjList
00408391      .  8B95 40FFFFFF            MOV EDX,DWORD PTR SS:[EBP-C0]                   ;  CrackmeV.00409A68
00408397      .  83C4 0C                  ADD ESP,0C
0040839A      .  8B82 00030000            MOV EAX,DWORD PTR DS:[EDX+300]
004083A0      .  56                       PUSH ESI
004083A1      .  8985 30FFFFFF            MOV DWORD PTR SS:[EBP-D0],EAX
004083A7      .  FFD0                     CALL EAX
004083A9      .  50                       PUSH EAX
004083AA      .  8D45 D8                  LEA EAX,DWORD PTR SS:[EBP-28]
004083AD      .  50                       PUSH EAX
004083AE      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet
004083B0      .  56                       PUSH ESI
004083B1      .  8985 58FFFFFF            MOV DWORD PTR SS:[EBP-A8],EAX
004083B7      .  FF95 38FFFFFF            CALL DWORD PTR SS:[EBP-C8]                      ;  MSVBVM50.0F10C340
004083BD      .  8D4D DC                  LEA ECX,DWORD PTR SS:[EBP-24]
004083C0      .  50                       PUSH EAX
004083C1      .  51                       PUSH ECX
004083C2      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet
004083C4      .  8BD8                     MOV EBX,EAX
004083C6      .  8D45 E8                  LEA EAX,DWORD PTR SS:[EBP-18]
004083C9      .  50                       PUSH EAX
004083CA      .  53                       PUSH EBX
004083CB      .  8B13                     MOV EDX,DWORD PTR DS:[EBX]                      ;  MSVBVM50.0F025A95
004083CD      .  FF92 A0000000            CALL DWORD PTR DS:[EDX+A0]
004083D3      .  85C0                     TEST EAX,EAX
004083D5      .  7D 12                    JGE SHORT CrackmeV.004083E9
004083D7      .  68 A0000000              PUSH 0A0
004083DC      .  68 AC6F4000              PUSH CrackmeV.00406FAC
004083E1      .  53                       PUSH EBX
004083E2      .  50                       PUSH EAX
004083E3      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
004083E9      >  8B8D 58FFFFFF            MOV ECX,DWORD PTR SS:[EBP-A8]
004083EF      .  8B55 E8                  MOV EDX,DWORD PTR SS:[EBP-18]
004083F2      .  52                       PUSH EDX
004083F3      .  8B19                     MOV EBX,DWORD PTR DS:[ECX]
004083F5      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004083FB      .  DC0D 10104000            FMUL QWORD PTR DS:[401010]                      ;  *3
00408401      .  83EC 08                  SUB ESP,8                                       ;  -2
00408404      .  DC25 18104000            FSUB QWORD PTR DS:[401018]
0040840A      .  DFE0                     FSTSW AX
0040840C      .  A8 0D                    TEST AL,0D
0040840E      .  0F85 AB030000            JNZ CrackmeV.004087BF
00408414      .  DD1C24                   FSTP QWORD PTR SS:[ESP]
00408417      .  FF15 48B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrR8>]      ;  MSVBVM50.__vbaStrR8
0040841D      .  8BD0                     MOV EDX,EAX
0040841F      .  8D4D E4                  LEA ECX,DWORD PTR SS:[EBP-1C]
00408422      .  FF15 94B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrMove>]    ;  MSVBVM50.__vbaStrMove
00408428      .  899D 2CFFFFFF            MOV DWORD PTR SS:[EBP-D4],EBX
0040842E      .  8B9D 58FFFFFF            MOV EBX,DWORD PTR SS:[EBP-A8]
00408434      .  50                       PUSH EAX
00408435      .  8B85 2CFFFFFF            MOV EAX,DWORD PTR SS:[EBP-D4]
0040843B      .  53                       PUSH EBX
0040843C      .  FF90 A4000000            CALL DWORD PTR DS:[EAX+A4]
00408442      .  85C0                     TEST EAX,EAX
00408444      .  7D 12                    JGE SHORT CrackmeV.00408458
00408446      .  68 A4000000              PUSH 0A4
0040844B      .  68 AC6F4000              PUSH CrackmeV.00406FAC
00408450      .  53                       PUSH EBX
00408451      .  50                       PUSH EAX
00408452      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
00408458      >  8D4D E4                  LEA ECX,DWORD PTR SS:[EBP-1C]
0040845B      .  8D55 E8                  LEA EDX,DWORD PTR SS:[EBP-18]
0040845E      .  51                       PUSH ECX
0040845F      .  52                       PUSH EDX
00408460      .  6A 02                    PUSH 2
00408462      .  FF15 80B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeStrList>>;  MSVBVM50.__vbaFreeStrList
00408468      .  83C4 0C                  ADD ESP,0C
0040846B      .  8D45 D8                  LEA EAX,DWORD PTR SS:[EBP-28]
0040846E      .  8D4D DC                  LEA ECX,DWORD PTR SS:[EBP-24]
00408471      .  50                       PUSH EAX
00408472      .  51                       PUSH ECX
00408473      .  6A 02                    PUSH 2
00408475      .  FF15 08B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaFreeObjList>>;  MSVBVM50.__vbaFreeObjList
0040847B      .  8B95 40FFFFFF            MOV EDX,DWORD PTR SS:[EBP-C0]                   ;  CrackmeV.00409A68
00408481      .  83C4 0C                  ADD ESP,0C
00408484      .  8B82 04030000            MOV EAX,DWORD PTR DS:[EDX+304]
0040848A      .  56                       PUSH ESI
0040848B      .  8985 28FFFFFF            MOV DWORD PTR SS:[EBP-D8],EAX
00408491      .  FFD0                     CALL EAX
00408493      .  50                       PUSH EAX
00408494      .  8D45 D8                  LEA EAX,DWORD PTR SS:[EBP-28]
00408497      .  50                       PUSH EAX
00408498      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet
0040849A      .  56                       PUSH ESI
0040849B      .  8985 58FFFFFF            MOV DWORD PTR SS:[EBP-A8],EAX
004084A1      .  FF95 30FFFFFF            CALL DWORD PTR SS:[EBP-D0]                      ;  MSVBVM50.0F10C348
004084A7      .  8D4D DC                  LEA ECX,DWORD PTR SS:[EBP-24]
004084AA      .  50                       PUSH EAX
004084AB      .  51                       PUSH ECX
004084AC      .  FFD7                     CALL EDI                                        ;  MSVBVM50.__vbaObjSet
004084AE      .  8BD8                     MOV EBX,EAX
004084B0      .  8D45 E8                  LEA EAX,DWORD PTR SS:[EBP-18]
004084B3      .  50                       PUSH EAX
004084B4      .  53                       PUSH EBX
004084B5      .  8B13                     MOV EDX,DWORD PTR DS:[EBX]                      ;  MSVBVM50.0F025A95
004084B7      .  FF92 A0000000            CALL DWORD PTR DS:[EDX+A0]
004084BD      .  85C0                     TEST EAX,EAX
004084BF      .  7D 12                    JGE SHORT CrackmeV.004084D3
004084C1      .  68 A0000000              PUSH 0A0
004084C6      .  68 AC6F4000              PUSH CrackmeV.00406FAC
004084CB      .  53                       PUSH EBX
004084CC      .  50                       PUSH EAX
004084CD      .  FF15 18B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaHresultCheck>;  MSVBVM50.__vbaHresultCheckObj
004084D3      >  8B8D 58FFFFFF            MOV ECX,DWORD PTR SS:[EBP-A8]
004084D9      .  8B55 E8                  MOV EDX,DWORD PTR SS:[EBP-18]
004084DC      .  52                       PUSH EDX
004084DD      .  8B19                     MOV EBX,DWORD PTR DS:[ECX]
004084DF      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004084E5      .  DC25 20104000            FSUB QWORD PTR DS:[401020]                      ;  TEMP -= -15
004084EB      .  83EC 08                  SUB ESP,8
004084EE      .  DFE0                     FSTSW AX
004084F0      .  A8 0D                    TEST AL,0D
004084F2      .  0F85 C7020000            JNZ CrackmeV.004087BF
........
00408677      . /74 62                    JE SHORT CrackmeV.004086DB
00408679      . |8B35 14B14000            MOV ESI,DWORD PTR DS:[<&MSVBVM50.__vbaStrCat>]  ;  MSVBVM50.__vbaStrCat
0040867F      . |68 C06F4000              PUSH CrackmeV.00406FC0                          ;  UNICODE "You Get It"
00408684      . |68 DC6F4000              PUSH CrackmeV.00406FDC                          ;  UNICODE "\r\n"
00408689      . |FFD6                     CALL ESI                                        ;  <&MSVBVM50.__vbaStrCat>
0040868B      . |8BD0                     MOV EDX,EAX
0040868D      . |8D4D E8                  LEA ECX,DWORD PTR SS:[EBP-18]
00408690      . |FF15 94B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrMove>]    ;  MSVBVM50.__vbaStrMove
00408696      . |50                       PUSH EAX
00408697      . |68 E86F4000              PUSH CrackmeV.00406FE8                          ;  UNICODE "KeyGen It Now"

Que se puede resumir en esto.

004081F5      .  FF15 F8B04000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaLenBstr>]    ;  MSVBVM50.__vbaLenBstr
004081FB      .  8BF8                     MOV EDI,EAX
004081FD      .  8B4D E8                  MOV ECX,DWORD PTR SS:[EBP-18]
00408200      .  69FF 385B0100            IMUL EDI,EDI,15B38                              ;  TEMP = Len(nombre) *15B38
00408206      .  51                       PUSH ECX
00408207      .  0F80 B7050000            JO CrackmeV.004087C4
0040820D      .  FF15 0CB14000            CALL DWORD PTR DS:[<&MSVBVM50.#516>]            ;  MSVBVM50.rtcAnsiValueBstr
00408213      .  0FBFD0                   MOVSX EDX,AX                                    ;  digito a ax
00408216      .  03FA                     ADD EDI,EDX                                     ;  TEMP +=1digito
00408218      .  0F80 A6050000            JO CrackmeV.004087C4
........
004082E9      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004082EF      .  D905 08104000            FLD DWORD PTR DS:[401008]
004082F5      .  833D 00904000 00         CMP DWORD PTR DS:[409000],0
004082FC      .  75 08                    JNZ SHORT CrackmeV.00408306
004082FE      .  D835 0C104000            FDIV DWORD PTR DS:[40100C]                      ;  10 / 5 = 2
00408304      .  EB 0B                    JMP SHORT CrackmeV.00408311
00408306      >  FF35 0C104000            PUSH DWORD PTR DS:[40100C]
0040830C      .  E8 578DFFFF              CALL <JMP.&MSVBVM50._adj_fdiv_m32>
00408311      >  83EC 08                  SUB ESP,8
00408314      .  DFE0                     FSTSW AX
00408316      .  A8 0D                    TEST AL,0D
00408318      .  0F85 A1040000            JNZ CrackmeV.004087BF
0040831E      .  DEC1                     FADDP ST(1),ST                                  ;  TEMP +=2
00408320      .  DFE0                     FSTSW AX
00408322      .  A8 0D                    TEST AL,0D
........
004083F5      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004083FB      .  DC0D 10104000            FMUL QWORD PTR DS:[401010]                      ;  TEMP *=3
00408401      .  83EC 08                  SUB ESP,8                                       ;  TEMP -=2
00408404      .  DC25 18104000            FSUB QWORD PTR DS:[401018]
0040840A      .  DFE0                     FSTSW AX
0040840C      .  A8 0D                    TEST AL,0D
........
004084DF      .  FF15 74B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaR8Str>]      ;  MSVBVM50.__vbaR8Str
004084E5      .  DC25 20104000            FSUB QWORD PTR DS:[401020]                      ;  TEMP -= -15
004084EB      .  83EC 08                  SUB ESP,8
004084EE      .  DFE0                     FSTSW AX
004084F0      .  A8 0D                    TEST AL,0D
004084F2      .  0F85 C7020000            JNZ CrackmeV.004087BF
........
00408677      . /74 62                    JE SHORT CrackmeV.004086DB
00408679      . |8B35 14B14000            MOV ESI,DWORD PTR DS:[<&MSVBVM50.__vbaStrCat>]  ;  MSVBVM50.__vbaStrCat
0040867F      . |68 C06F4000              PUSH CrackmeV.00406FC0                          ;  UNICODE "You Get It"
00408684      . |68 DC6F4000              PUSH CrackmeV.00406FDC                          ;  UNICODE "\r\n"
00408689      . |FFD6                     CALL ESI                                        ;  <&MSVBVM50.__vbaStrCat>
0040868B      . |8BD0                     MOV EDX,EAX
0040868D      . |8D4D E8                  LEA ECX,DWORD PTR SS:[EBP-18]
00408690      . |FF15 94B14000            CALL DWORD PTR DS:[<&MSVBVM50.__vbaStrMove>]    ;  MSVBVM50.__vbaStrMove
00408696      . |50                       PUSH EAX
00408697      . |68 E86F4000              PUSH CrackmeV.00406FE8                          ;  UNICODE "KeyGen It Now"

Y en esto:

TEMP = Len(nombre) *15B38
TEMP += 1ºdigitoascii
TEMP +=2
TEMP *=3
TEMP -=2
TEMP +=15

 Y el KeyGen nos ocupa una sola línea

txtserial.Text = (((((Len(txtnombre.Text) * 88888) + Asc(Mid(txtn.Text, 1, 1))) + 2) * 3) - 2) + 15

 Huevo de pascua (Easter egg)

Si nos fijamos en el VBReformer, en el formulario principal vemos muchas cajas de texto.

vbreformervistaproject

Las hacemos visibles, guardamos y ejecutamos haber que pasa.

textsvisibles

crackmebonus

Lo que pasa es que va guardando el resultado de las operaciones en ellas y en la de arriba concretamente está nuestro serial bueno, lo que nos hace poseedores de un KeyGen encubierto.

Links

TDC's Remove the NAG - Parche
Intro Es un crackme realizado en ensamblador y en el que el objetivo es remover la NAG de la forma
Solución a los retos javascript de rogerfm.net
Introducción Javascript 1 (Serial a la vista) Javascript 2 (La función charAt()) Javascript 3 (Input) Javascript 4 (Fuerza bruta manual) Javascript
Solución al PGC Official KeygenMe
Introducción Siguiendo con los crackmes que contienen RSA, esta vez tenemos un Keygenme del grupo PGC (Pirates Gone Crazy) que
Blooper Tech Movie VII – Absentia 1×06 (S01E06)
En el BTM anterior nos remontábamos al año 2006 para ver un pequeño gazapo ocurrido en la serie Dexter. En

Tron – Reto IA de yoire.com

por ·1 comentario

Introducción

Hace tiempo que me aficioné a los retos de Hacking y Cracking, y si bien la mayoría de ellos consisten en desencriptar una clave o realizar ingeniería inversa sobre un ejecutable, también los hay sobre programación pura y dura.

En esta ocasión se nos proporciona un código «muestra» parecido a PHP o C++ y tenemos que ingeniarnoslas para mejorarlo y ganar a la máquina.

Objetivo del juego y normas

El objetivo de esta misión es ganar a Tr0n en su propio juego: las carreras de motos. Se te proporcionará un programa (código) funcional para que veas como se controla el vehiculo. Usando tu inteligencia, tendrás que entender su uso y mejorarlo, ya que no es lo suficientemente bueno como para ganar a Tr0n. Tr0n lleva ya bastante tiempo en la parrilla de juegos y es bastante habilidoso 🙂

Cuando venzas a Tr0n un mínimo de 5 veces consecutivas, se te dará por superada esta prueba.

Buena suerte!!!

[ Available functions / Funciones disponibles ]
direction() returns current direction, change to a new one with direction([newdir])
getX(), getY() returns X and Y coordinates
collisionDistance() | collisionDistance([anydir]) returns the distance until collision
Note: parameters [*dir] can be empty or one of this values: UP DOWN LEFT or RIGHT

[ Constants / Constantes ]
UP DOWN LEFT RIGHT MAX_X MAX_Y

[ Rules / Reglas ]
Try to survive driving your bike and … / Intenta sobrevivir conduciendo tu moto y…
Don’t cross any line / No cruces ninguna línea
or crash with the corners! / o choques con las esquinas!

[ Mission / Mision ]
Use well this controller and beat Tr0n 5 consecutive times to score in this game
Usa bien este controlador y vence a Tr0n 5 veces consecutivas para puntuar en este juego

Código inicial

Nada más comenzar vemos que hemos perdido nuestra primera partida con el siguiente código:

	function controller(playerController $c){
		if($c->direction()==UP && $c->getY()<10){
			if(rand(0,1)==0) $c->direction(LEFT);
				else $c->direction(RIGHT);
			goto done;
		}
		if($c->direction()==DOWN && MAX_Y-$c->getY()<10){
			if(rand(0,1)==0) $c->direction(LEFT);
				else $c->direction(RIGHT);
			goto done;
		}
		if($c->direction()==LEFT && $c->getX()<10){
			if(rand(0,1)==0) $c->direction(UP);
				else $c->direction(DOWN);
			goto done;
		}
		if($c->direction()==RIGHT && MAX_X-$c->getX()<10){
			if(rand(0,1)==0) $c->direction(UP);
				else $c->direction(DOWN);
		}
		done:
	}

Nosotros somos el AZUL y la máquina es el VERDE.

loose_inicial

Primeras modificaciones

Lo primero que tenemos que modificar son las distancias de las coordenadas que estan puestas en «<10» al mínimo, que sería «<2«. También sustituir la aleatoriedad «rand(0,1)==0» por algo más útil y comenzar a usar la función «collisionDistance()«.

Como podéis observar en el código inferior, usamos la función «collisionDistance()» para detectar cuando estamos a punto de chocar «collisionDistance() ==1» y para detectar a que lado nos conviene más girar en función de donde podamos recorrer más distancia «if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT); else $c->direction(RIGHT);«.

if($c->direction()==UP && $c->getY()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
		}
if($c->direction()==DOWN && MAX_Y-$c->getY()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
		}
if($c->direction()==LEFT && $c->getX()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) 
                                $c->direction(UP);
				else 
                                $c->direction(DOWN);
		}
if($c->direction()==RIGHT && MAX_X-$c->getX()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) $c->direction(UP);
				else $c->direction(DOWN);
				
		}

Terminando la faena

El código anterior de por sí no nos resuelve mucho si no afinamos un poco más, comprobando todos las posibles colisiones y tomando la dirección correcta en función de la mayor distancia a recorrer.

    if($c->collisionDistance([UP])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([DOWN])==1 || $c->collisionDistance() ==1){
            if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([RIGHT])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
     if($c->collisionDistance([LEFT])==1 || $c->collisionDistance() ==1){
          if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }

Código ganador

El código que utilicé yo para ganar a Tron es el siguiente:

function controller(playerController $c){
uno:
if($c->direction()==UP && $c->getY()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
				
		}
if($c->direction()==DOWN && MAX_Y-$c->getY()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
				
		}
if($c->direction()==LEFT && $c->getX()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) 
                                $c->direction(UP);
				else 
                                $c->direction(DOWN);
				
		}
if($c->direction()==RIGHT && MAX_X-$c->getX()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) $c->direction(UP);
				else $c->direction(DOWN);
				
		}
dos:
    if($c->collisionDistance([UP])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([DOWN])==1 || $c->collisionDistance() ==1){
            if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([RIGHT])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
     if($c->collisionDistance([LEFT])==1 || $c->collisionDistance() ==1){
          if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
		done:
	}

Mis jugadas ganadoras:

01

02

03

04

05

El código no es infalible ya que como comprabaréis vosotros mismos, no se puede ganar siempre por el mero hecho de la aleatoriedad y de la suerte. Cuando dispongais de un código decente, ejecutarlo varias veces para estar seguros antes de desecharlo.

Curiosidades

Como se suele decir, la banca siempre gana, y en este caso no iba a ser menos y es que en caso de empate ¡la banca gana!

empate

 

Por último deciros que podéis utilizar el código ya que la web detecta los códigos ganadores para que no se repitan.

Enlaces

Blooper Tech Movie VIII – Black Mirror 4×05 (MetalHead)

por ·1 comentario

Hoy tenemos aquí un capitulo del gran David Slade, productor de Series como American Gods o Hannibal y director de películas como Hard Candy o 30 días de oscuridad.

El guiño

Lo que más me ha gustado del capítulo es el guiño que han hecho a la RaspBerry PI. La escena transcurre al inicio del capítulo cuando uno de los protagonistas se conecta a un vehículo para hackearlo con una Raspi 3 Model B con varios pines del GPIO doblados. Os dejo unas capturas a continuación donde se aprecia el logo.

La conexión

Ya puestos, la conexión parece micro usb tipo B. Al fondo se ve lo que parece un puerto HDMI.

La pifia

Lo que no me ha gustado es que al fijarme en el software que corre en el vehículo aparece un flamante OMNIBOOT.EXE con un aspecto parecido al símbolo de sistema, es decir, nos intentan vender que en un futuro el software que gestiona el vehículo es alguna variación de Windows, algo poco probable a día de hoy al menos. Con este tipo de predicciones no se puede escupir hacia arriba pero actualmente es más probable un nucleo tipo Linux u otro propietario al estilo Tesla.

Software del vehículo

Software del vehículo

Os dejo todas las capturas relevantes a continuación.

Tras las Pantallas de ‘Contact’: Un Viaje a Través del Hardware y del Software

por ·Sin comentarios

Introducción

La película «Contact«, estrenada en 1997 y dirigida por Robert Zemeckis, es una adaptación de la novela homónima de Carl Sagan. Más allá de su profunda exploración sobre la existencia de vida extraterrestre y el debate entre ciencia y fe, la película ofrece un interesante vistazo a la tecnología de la época. En este análisis, nos enfocaremos en los aspectos tecnológicos presentes en la película, detallando los sistemas operativos, software y hardware utilizados por los protagonistas.

Sinopsis

La Dra. Eleanor «Ellie» Arroway, interpretada por Jodie Foster, es una científica dedicada al proyecto SETI (Búsqueda de Inteligencia Extraterrestre). Tras años de búsqueda, capta una señal proveniente del espacio profundo que contiene instrucciones para construir una máquina enigmática. A medida que se desarrolla la trama, Ellie enfrenta desafíos políticos, religiosos y personales mientras lucha por interpretar el mensaje y lo que podría significar para la humanidad.

Análisis Tecnológico

Sistemas Operativos y Software

Uno de los aspectos más destacados en Contact es la presencia del sistema operativo UNIX. A lo largo de la película, se observan pistas que indican su uso, como pegatinas en las pantallas con mensajes del estilo: «Join the UNIX PARTY (The open system platform)». UNIX, desarrollado en la década de 1970, es conocido por su estabilidad y eficiencia, características esenciales en entornos científicos y de investigación.

La utilización de Netscape Navigator es recurrente. El logo de Netscape aparece en varias ocasiones, especialmente durante las videoconferencias que se muestran sin retrasos apreciables. Netscape fue uno de los primeros navegadores web ampliamente utilizados y jugó un papel crucial en la expansión de Internet durante los años 90.

Es importante destacar que, aunque la película promueve la idea de sistemas abiertos a través del uso de UNIX, Netscape Navigator no era software libre en el momento en que se rodó la película. Durante esa época, antes de 1997, Netscape era un navegador propietario. Sin embargo, en sistemas UNIX, Netscape tenía poca competencia y era el navegador predominante, soportando estándares abiertos como HTTP y HTML. Curiosamente, en 1998, poco después del estreno de la película, Netscape liberó el código fuente de su navegador, iniciando el proyecto Mozilla y contribuyendo significativamente al movimiento del software libre.

El software o plataforma denominada MADDEN HADDEN es utilizado por los protagonistas en diversas localizaciones, sugiriendo que es un estándar en su campo. Aunque en la realidad no existe un software conocido con ese nombre en el ámbito científico, en la película parece ser una herramienta integral para el análisis de datos y comunicación.

Videoconferencias y Comunicaciones

Las videoconferencias sin «lags» (retrasos) que se muestran en la película son notables, especialmente considerando las limitaciones tecnológicas de la época. La presencia del logo de Netscape durante estas comunicaciones resalta el optimismo sobre las capacidades de Internet en 1997. En ese entonces, las conexiones de alta velocidad no eran comunes, y las videollamadas de calidad eran más una aspiración que una realidad.

Estándares y Sistemas Abiertos

La promoción de sistemas abiertos es evidente en la película. El uso de UNIX, basado en estándares abiertos, refleja una filosofía de colaboración y accesibilidad en el ámbito científico. Aunque Netscape Navigator no era software libre durante la producción de la película, su soporte para estándares abiertos de Internet lo convirtió en una herramienta esencial para la comunicación y el intercambio de información entre científicos y profesionales.

Hardware

En términos de hardware, la película presenta una variedad de equipos representativos de la tecnología de los años 90:

Monitor NEC MultiSync XE21: Un monitor CRT de 21 pulgadas conocido por su alta resolución y calidad de imagen, ideal para aplicaciones que requieren detalles precisos.

Monitores con marcas ocultas: Es interesante notar que en varios monitores se utilizan post-its o adhesivos para cubrir la marca y el modelo. Esto podría deberse a decisiones de producción para evitar publicidad no deseada o cuestiones legales relacionadas con derechos de marca.

Monitor CTX: Aunque no se especifica el modelo, los monitores CTX eran populares por su fiabilidad y rendimiento a un costo razonable.

Monitor Hansol Mazellan 17px: Los monitores Hansol eran reconocidos por su calidad en la reproducción de gráficos, siendo utilizados en diseño y aplicaciones multimedia.

Monitor IBM: IBM fue pionera en tecnología informática, y sus monitores eran sinónimo de calidad y durabilidad. Aunque no se especifica el modelo exacto, es probable que se trate de uno de sus populares monitores CRT utilizados en entornos profesionales.

Evolución de UNIX y Windows

Para entender el contexto tecnológico de la época, es útil comparar la evolución de UNIX y Windows, así como de los navegadores Netscape Navigator e Internet Explorer.

Detalles Adicionales

Cobertura de marcas: La práctica de cubrir las marcas y modelos en los monitores podría indicar un intento de la producción por crear un entorno más universal y atemporal, evitando asociar la tecnología presentada con productos específicos que podrían quedar obsoletos rápidamente. En bastantes fotogramas se nota que esto es completamente intencionado.

Representación de la tecnología: La película equilibra la precisión técnica con las necesidades narrativas. Si bien algunas representaciones, como las videoconferencias fluidas, eran tecnológicamente avanzadas para la época, sirven para enfatizar la conectividad y colaboración global entre los científicos.

SETI y la Búsqueda de Vida Extraterrestre: En Contact, la Dra. Ellie Arroway dedica su vida al proyecto SETI (Search for Extraterrestrial Intelligence), reflejando el esfuerzo real de la comunidad científica por encontrar señales de inteligencia extraterrestre. SETI es una iniciativa internacional que utiliza radiotelescopios para detectar posibles comunicaciones de civilizaciones fuera de la Tierra. La película captura la pasión y los desafíos asociados con este tipo de investigación, destacando la dedicación de los científicos que trabajan en el límite de lo conocido.

El Mensaje de Arecibo: El radiotelescopio de Arecibo en Puerto Rico juega un papel significativo tanto en la realidad como en la película. En 1974, desde este observatorio, se envió el famoso Mensaje de Arecibo, una transmisión de radio dirigida al cúmulo estelar M13, diseñada para demostrar los avances tecnológicos humanos y nuestra existencia a posibles civilizaciones extraterrestres. El mensaje contenía información codificada sobre la composición humana, nuestro sistema numérico, la estructura del ADN y nuestra posición en el sistema solar. En «Contact», aunque la señal recibida por Ellie proviene de Vega y no está directamente relacionada con el Mensaje de Arecibo, la película establece paralelismos con este acontecimiento histórico. La utilización de Arecibo como escenario subraya la conexión entre los esfuerzos reales y ficticios en la búsqueda de inteligencia extraterrestre. La película explora la posibilidad de que, así como enviamos mensajes al espacio, podríamos recibir respuestas o comunicaciones de otras civilizaciones.

Matthew McConaughey: Es interesante notar cómo este actor ha participado en dos de las películas más destacadas de la ciencia ficción: Contact e Interstellar. En Contact, McConaughey interpreta un papel secundario como Palmer Joss, un escritor y asesor espiritual que cuestiona las implicaciones éticas y filosóficas del descubrimiento científico. Diecisiete años después, en Interstellar, asume el rol protagonista de Cooper, un ex piloto de la NASA que emprende una misión interestelar para salvar a la humanidad.

Números primos: El inicio de la investigación seria de la señal extraterrestre en la película se desencadena cuando, al analizar la señal recibida, los científicos descubren que esta codifica una secuencia de números primos. Este hallazgo resulta crucial, ya que los números primos, al ser divisibles únicamente por 1 y por sí mismos, no surgen de forma aleatoria en procesos naturales conocidos. Su presencia en la señal sugiere intencionalidad e inteligencia detrás de su emisión, lo que confirma que no se trata de ruido cósmico sino de una posible comunicación deliberada desde una civilización avanzada. Este descubrimiento impulsa a los científicos a profundizar en la decodificación, marcando el verdadero inicio de la búsqueda de vida extraterrestre.

Conclusión

Contact no solo es una obra que invita a reflexionar sobre nuestro lugar en el universo y la posibilidad de vida más allá de la Tierra, sino que también es un retrato de la tecnología de su tiempo. La inclusión de sistemas operativos como UNIX, navegadores como Netscape y hardware específico refleja una atención al detalle que enriquece la narrativa. A pesar de que Netscape Navigator no era software libre durante la producción de la película, su presencia destaca la importancia de los estándares abiertos y la colaboración en el avance científico.

También destaca por su compromiso con la precisión científica, en gran parte debido a la influencia de Carl Sagan, autor de la novela original y asesor en la producción. La representación de los procedimientos del SETI, el análisis de señales y las discusiones éticas y filosóficas reflejan debates reales en la comunidad científica. La inclusión de elementos como el Mensaje de Arecibo y las operaciones del radiotelescopio añaden autenticidad a la narrativa y acercan al público a la realidad de la exploración espacial.

Bibliografía y Enlaces

Galería

Guía rápida para tener una red Gigabit en casa

por ·1 comentario

Introducción

Un día cualquiera se te ocurre comprarte un disco duro de red NAS para centralizar todo tu contenido multimedia. Lo conectas y todo va genial, pero de repente vas a copiar unos cuantos gigas de fotos y te encuentras con que la operación va a tardar días. En ese mismo instante te planteas sacar el máximo provecho a tu red doméstica y la solución se llama gigabit.

A quién va dirigido

Esta guía va dirigida a todo el mundo que esté pensando en hacer o mejorar la red LAN doméstica. Si eres un amante del WIFI, olvídate de esto, ya que para conseguir altas velocidades se necesita cablear la casa. Además, de lo que trata esta guía es de que se conecte un ordenador portátil o sobremesa de la forma más rápida posible al disco duro de red.

Comprobaciones previas

Probablemente dispongas de un Modem / Router proporcionado por tu compañia y que seguramente no sea gigabit (10/100/1000), esto es lo primero que debes comprobar. Busca tu modelo en internet y cerciorate.

También necesitas que la tarjeta de red del portátil o sobremesa sean gigabit, en este caso lo más probable es que lo sean pero asegúrate.

Lo que necesitamos

Tras hacer las comprobaciones previas ya podemos hacer una lista de los materiales que necesitamos.

  • Router gigabit (en caso del que tu compañia no lo sea).

Si el nuestro no es gigabit existen soluciones económicas como el TP-Link TL-WR1043ND que lo tenemos por 44€ en pccomponentes. Os recomiendo esta tienda por rapidez, seriedad y no abusan con los gastos de envío.

tp_link_tl_wr1043nd_ultimate_router_neutro_wifi_11n_usb_4

  • Switch gigabit (para ampliar puertos)

En caso de que los cuatro puertos que vienen con el router se nos queden cortos, la solución más economica y acertada es un Switch ethernet gigabit como el TP-LINK TL-SG1005D que lo tenemos por 16€. Este dispositivo es una maravilla ya que nos brinda 4 puertos más y no requiere configuración alguna.

tp_link_tl_sg1005d_switch_5_puertos_gigabit

  • Tarjeta de red gigabit (para pc sobremesa en caso de no ser o no disponer)

Son muy económicas, las puedes encontrar por 10€-15€ en cualquier tienda especializada. Ejemplo PCI. Ejemplo PCI-e. Video instalación de una tarjeta de red.

tarjeta-de-red-tp-link-tg-3269-gigabit-pci-internet-101000-1859-MLU4520989306_062013-F

  • Bobina de cable de red Categoría 6.

100m de cable UTP categoría 6 viene a costar sobre unos 42€.

bobina_100m_cable_red_rigido_utp_cat_6_10_100_1000

  • Cables Cat6 interconexionado router / switch / pc.

Para interconexionado de equipos recomiento estos de 50cm por 1,5€. Para conexión del pc tienes otras larguras más apropiadas. También podéis haceros vosotros los cables con lo sobrante de la bobina, para ello necesitaréis una crimpadora y terminales rj45.

digitus_cable_de_red_rj45_cat_6_10_100_1000_gris__50cm_

  • Tomas RJ45 categoría 6.

Esto depende de tu instalación y la gama que elijas. En mi caso utilizo tomas Niessen que solo el conector vale 16€, pero tienes tomas más económicas. De superficie por 2,75€ y empotrable por 8,25€.

roseta_de_superficie_cat6_conector_red_hembra_rj45 roseta_empotrable_cat5e_2_conectores_red_45__hembra_rj_45

  • Insertadora (punch down) para las tomas RJ45.

Indispensable para conectar internamente los cables de las tomas. La tenéis por 11€ en ebay. Video de la insertadora en acción.

PCS058007_large

  • Disco duro de red NAS

Esto es una recomendación personal ya que la elección puede variar en función de las necesidades de almacenamiento y conexiones. Una solución barata y con espacio suficiente para uso doméstico es el disco WD My Cloud 3TB que lo podeis adquirir por 159€.

wd_my_cloud_4tb

Presupuesto (Precios Octubre 2014)

  • Router = 44€
  • Switch = 16€
  • Tarjeta de red = 15€
  • Bobina de cable = 42€
  • Cables interconexionado 50cm x4 = 6€
  • Cable conexión pc / switch o router 1,8m = 2,95€
  • Tomas RJ45 x 2 = 16,5€
  • Disco duro de red NAS = 159€
  • TOTAL = 345,45€ + gastos de envío.

Esto puede variar en función de los componentes que elijas comprar pero el coste oscilará entre 250 y 350€, algo bastante asequible para centralizar contenido multimedia. Digo asequible por que la mitad del presupuesto se lo lleva el disco de red, los componentes son más bien baratos.

Ejemplo de instalación

Esquema inicial

En mi esquema disponemos del router proporcionado por el proveedor de internet que en mi caso sí es gigabit pero que solo lo utilizo para dar internet al router neutro.El router neutro junto con el switch me proporcionan 8 puertos gigabit. El router neutro además gestiona el wifi de la casa, pero en el mejor de los casos (Wifi n) estos dispositivos solo podrán mover datos a 300mbps. Utilizo como media center mis amadas Raspberry Pi que en este caso no se benefician de la velocidad ya que disponen de conexión 10/100.

esquema

Configurar router neutro

Lo primero a conectar es el router neutro y en este caso, TP-Link te lo pone fácil si no te defiendes muy bien con las redes, ya que proporciona un CD que se encarga de guiarte paso a paso. Lo más importante es la asignación de la IP privada, por defecto es 192.168.2.1 y a no ser que el router de la compañia tenga esa misma IP lo podéis dejar como está.

Disco duro de red NAS

Para configurar el disco de red normalmente viene un CD para ayudar al usuario novel. Lo único que tenéis que tener en cuenta es que la IP debe estar en consonancia con la del router neutro, si el router neutro es 192.168.2.1 al disco NAS podéis asignarle 192.168.2.150. Para más información aquí tenéis la guía de instalación.

Preguntas frecuentes. FAQ

  • ¿El cable normal o cruzado?

Podéis usar cable normal, también llamado conexión Pin a Pin ó 1:1, para toda la instalación ya que los dispositivos de hoy en día aceptan cualquier cable y resuelven internamente en función del cable conectado. Pero si nos ponemos quisquillosos, para conectar elementos pasivos entre sí (router a switch, etc) se utiliza cable normal 1:1. Para conectar elementos activos (PC a router/switch) cable cruzado.

  • ¿Qué norma de colores uso?

Mi consejo es que uses el standard EIA/TIA 568B tanto en la conexión de las cajas como en la creación de los cables.

image002

Cada roseta o toma en su interior tiene definido el orden que debes seguir para conectar los cables según el standard A o B, esto es una aproximación y puede no coincidir con tu toma.

con_roseta

  • Tengo todo instalado y es categoría 6 pero mi pc me marca que me conecta a 100mbps ¿qué pasa?

Si estás seguro de que las rosetas están bien conectadas, que has usado los cables correctos, que todos los dispositivos son gigabit y tu pc hace de las suyas, quizás debas de forzar a tu tarjeta de red a trabajar en modo gigabit ó 100 full duplex ó 100FD. Esto es debido a que el driver de la tarjeta de red por defecto viene con la opción de «autonegociación» activada y a veces necesita que le «obligues» a trabajar en gigabit.

En cada tarjeta de red puede venir diferente, yo os muestro mi caso desde windows 7:

Diríjete a Inicio > Panel de control > Ver el estado y las tareas de red > conexión de area local

En mi caso marca 1 Gbps pero si estais teniendo problemas os marcará 100 mbps. A continuación pulsa Propiedades.

31-10-2014 21-47-55

Pulsa Configurar.

31-10-2014 21-49-19

En la pestaña Opciones avanzadas busca la opción de la velocidad, en mi caso «Speed/duplex settings» y selecciona 100 mb Full Duplex. De este modo le forzais a la tarjeta de red a trabajar en modo gigabit. Si no lo consiguiera trabajará en el modo que pueda pero no os dejará sin conexión.

31-10-2014 21-50-31

Glosario

  1. NAS – del inglés Network Attached Storage, es el nombre dado a una tecnología de almacenamiento dedicada a compartir la capacidad de almacenamiento a través de una red. Estos discos vienen equipados como mínimo con una conexión RJ45 para integrarlo en una red de forma rápida y sencilla.
  2. Full Duplex – Que transmite y recibe en ambas direcciones al mismo tiempo por cables independientes.
  3. Switch – Un conmutador o switch es un dispositivo digital lógico de interconexión de equipos que opera en la capa de enlace de datos del modelo OSI. Su función es interconectar dos o más segmentos de red, de manera similar a los puentes de red, pasando datos de un segmento a otro de acuerdo con la dirección MAC de destino de las tramas en la red.
  4. Gigabit Ethernet – también conocida como GigaE, es una ampliación del estándar Ethernet (concretamente la versión 802.3ab y 802.3z del IEEE) que consigue una capacidad de transmisión de 1 gigabit por segundo, correspondientes a unos 1000 megabits por segundo de rendimiento contra unos 100 de Fast Ethernet (También llamado 100BASE-TX).

Notas finales

Soy consciente de que me he dejado muchas cosas en el tintero pero mi pretensión es que el lector de un vistazo rápido tenga una idea clara de lo que necesita para lograr una red decente en casa.