Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
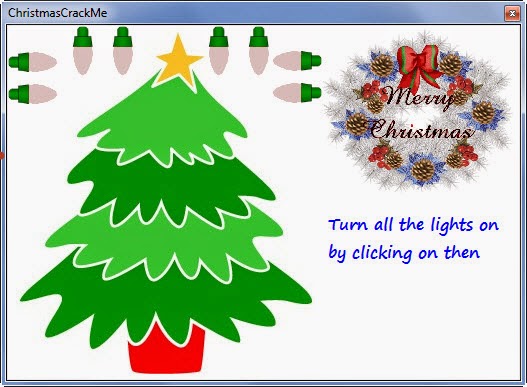
Intro
This crackme is for the crack challenge 6 of canyouhack.it.
In this crackme the goal is to turn on all the lights. Note that a light off to the next, so if we interrupt this, we win.
Tools
Exeinfo (For crackme info)
Delphi Decompiler (For decompile)
OllyDbg (For debug)
Decompiling
With Delphi Decompiler we can found easy the buttons and his offsets.
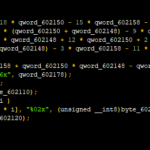
Go to the offset 401A64 in OllyDbg and analyze the code.
We view two jumps, one turn ON the light and the other Turn OFF the next light. Patching the call from offset 401A8B we get the serial.
Continuamos con la segunda entrega de Cruehead. En este caso nos encontramos con un único campo de contraseña para introducir.
El algoritmo
Abrimos con Olly y vemos dos saltos. El primer Call realiza una serie de operaciones con el serial introducido y el segundo comprueba si el serial es correcto.
A continuación llegamos aquí:
00401365 /$ C605 18214000 00 MOV BYTE PTR DS:[402118],0
0040136C |. 8B7424 04 MOV ESI,DWORD PTR SS:[ESP+4]
00401370 |. 56 PUSH ESI
00401371 |> 8A06 /MOV AL,BYTE PTR DS:[ESI] ; <---
00401373 |. 84C0 |TEST AL,AL
00401375 |. 74 19 |JE SHORT CRACKME2.00401390
00401377 |. FE05 18214000 |INC BYTE PTR DS:[402118]
0040137D |. 3C 41 |CMP AL,41 ; 41 = A
0040137F |. 72 04 |JB SHORT CRACKME2.00401385 ; ya es mayúscula
00401381 |. 3C 5A |CMP AL,5A ; 5A = Z
00401383 |. 73 03 |JNB SHORT CRACKME2.00401388 ; Convertir a mayúscula
00401385 |> 46 |INC ESI
00401386 |.^ EB E9 |JMP SHORT CRACKME2.00401371 ; Bucle -->
00401388 |> E8 25000000 |CALL CRACKME2.004013B2
0040138D |. 46 |INC ESI
0040138E |.^ EB E1 \JMP SHORT CRACKME2.00401371
00401390 |> 5E POP ESI
00401391 |. E8 03000000 CALL CRACKME2.00401399 ;Convertido a mayúsculas continuamos
00401396 |. EB 00 JMP SHORT CRACKME2.00401398
00401398 \> C3 RETN
Si nuestro serial contiene solo letras, las convierte a mayúsculas y seguimos aquí. En resumen hace XOR byte a byte entre nuestro serial y la frase «Messing_in_bytes»
00401399 /$ 33DB XOR EBX,EBX
0040139B |. 33FF XOR EDI,EDI
0040139D |> 8A8F A3214000 /MOV CL,BYTE PTR DS:[EDI+4021A3] ; Carga el primer byte de 4021A3
004013A3 |. 8A1E |MOV BL,BYTE PTR DS:[ESI] ;
004013A5 |. 84DB |TEST BL,BL
004013A7 |. 74 08 |JE SHORT CRACKME2.004013B1
004013A9 |. 32D9 |XOR BL,CL ; byteSerial XOR Byte"Messing_in..."
004013AB |. 881E |MOV BYTE PTR DS:[ESI],BL
004013AD |. 46 |INC ESI ;Siguiente byte de "Messing_in_bytes"
004013AE |. 47 |INC EDI ;Siguiente byte del serial
004013AF |.^ EB EC \JMP SHORT CRACKME2.0040139D
004013B1 \> C3 RETN ;XOR finalizado volvemos
Estado del DUMP (memoria) antes del XOR y con nuestro serial (12345678) cargado.
Si buscamos el comando REPE encontramos que si el flag Z = 1 el bucle se corta y que trabaja con bytes. El problema es que en Olly la instrucción REPE nosotros la vemos con un solo paso y nos puede pasar desapercibida.
En resumen, está comprobando los bytes de las direcciones 402150 (1F 2C 37 36 3B 3D 28 19 3D 26 1A 31 2D 3B 37 3E) con nuestro serial XOReado, 40217E en adelante, por lo que si hacemos XOR entre los bytes de 402150 y la frase «Messing_in_bytes» obtendremos la clave correcta.
M e s s i n g _ i n _ b y t e s
4D 65 73 73 69 6E 67 5F 69 6E 5F 62 79 74 65 73
XOR
1F 2C 37 36 3B 3D 28 19 3D 26 1A 31 2D 3B 37 3E
-----------------------------------------------
52 49 44 45 52 53 4F 46 54 48 45 53 54 4F 52 4D
R I D E R S O F T H E S T O R M
Serial: RIDERSOFTHESTORM
Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.
Análisis inicial
El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.
Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.
Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.
Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.
ChatGPT
resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos
Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:
Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.
Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.
El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.
Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.
Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.
El código
Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.
soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)
for x in rango_valores_x:
for y in rango_valores_y:
for z in rango_valores_z:
# Calculamos el valor de la expresión para cada combinación de x, y, z
valor = x / (y + z) + y / (x + z) + z / (x + y)
# Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
if abs(valor - 4) < 1e-6: # Usamos una pequeña tolerancia para evitar errores de precisión
soluciones.append((x, y, z))
print(soluciones)
Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.
En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.
¿Qué está pasando?
Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.
Curvas elípticas
Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.
Adecuación
Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.
Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.
\begin{align}
& y^2=x^3+109x^2+224x\\
\end{align}
donde:
\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}
Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.
Mathematica
El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos.
(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva,
o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] :=
If[x1 == x2 && y1 == y2,
ImplicitD[curve4, y, x] /. {x -> x1, y -> y1},
(y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos
o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1;
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] :=
{Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2,
-Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] :=
{(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)),
(8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)),
(-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución
válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n,
NestWhile[nextRational4[#, P4] &, P4,
! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]
Solución
Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.
ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.
Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.
Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en activo y por lo tanto no se debería resolver utilizando esta información.
Realistic Challenge 5: There is a new company out called NullCo. Have a look around the site and see what you can do.
Hay una nueva compañia llamada NullCo. Echa un vistazo a la web haber que puedes hacer.
Analizando a la víctima
Echamos un vistazo a la web y lo único interesante que vemos es un buscador.
Miramos el código fuente y vemos una ruta interesante.
Si exploramos la ruta «http://www.thisislegal.com/nc/adm/» nos aparece un login. Metemos cualquier cosa y el mensaje de error da demasiada información.
Ahora fijémonos en el menú productos. Pinchamos sobre cualquier producto y a continuación en la imagen para ampliarla, veremos el siguiente enlace.
Vamos a ver si podemos explotar «i.php«. Probamos a obtener información sensible del servidor.
Probamos «http://www.thisislegal.com/nc/i.php?img=adm/login.pwd» y nos da error, seguramente por que está anexionando la extensión de la imagen, es decir, el script está interpretando esto:
Hace tiempo que me aficioné a los retos de Hacking y Cracking, y si bien la mayoría de ellos consisten en desencriptar una clave o realizar ingeniería inversa sobre un ejecutable, también los hay sobre programación pura y dura.
En esta ocasión se nos proporciona un código «muestra» parecido a PHP o C++ y tenemos que ingeniarnoslas para mejorarlo y ganar a la máquina.
Objetivo del juego y normas
El objetivo de esta misión es ganar a Tr0n en su propio juego: las carreras de motos. Se te proporcionará un programa (código) funcional para que veas como se controla el vehiculo. Usando tu inteligencia, tendrás que entender su uso y mejorarlo, ya que no es lo suficientemente bueno como para ganar a Tr0n. Tr0n lleva ya bastante tiempo en la parrilla de juegos y es bastante habilidoso 🙂
Cuando venzas a Tr0n un mínimo de 5 veces consecutivas, se te dará por superada esta prueba.
Buena suerte!!!
[ Available functions / Funciones disponibles ]
direction() returns current direction, change to a new one with direction([newdir])
getX(), getY() returns X and Y coordinates
collisionDistance() | collisionDistance([anydir]) returns the distance until collision
Note: parameters [*dir] can be empty or one of this values: UP DOWN LEFT or RIGHT
[ Constants / Constantes ]
UP DOWN LEFT RIGHT MAX_X MAX_Y
[ Rules / Reglas ]
Try to survive driving your bike and … / Intenta sobrevivir conduciendo tu moto y…
Don’t cross any line / No cruces ninguna línea
or crash with the corners! / o choques con las esquinas!
[ Mission / Mision ]
Use well this controller and beat Tr0n 5 consecutive times to score in this game
Usa bien este controlador y vence a Tr0n 5 veces consecutivas para puntuar en este juego
Código inicial
Nada más comenzar vemos que hemos perdido nuestra primera partida con el siguiente código:
Lo primero que tenemos que modificar son las distancias de las coordenadas que estan puestas en «<10» al mínimo, que sería «<2«. También sustituir la aleatoriedad «rand(0,1)==0» por algo más útil y comenzar a usar la función «collisionDistance()«.
Como podéis observar en el código inferior, usamos la función «collisionDistance()» para detectar cuando estamos a punto de chocar «collisionDistance() ==1» y para detectar a que lado nos conviene más girar en función de donde podamos recorrer más distancia «if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT); else $c->direction(RIGHT);«.
El código anterior de por sí no nos resuelve mucho si no afinamos un poco más, comprobando todos las posibles colisiones y tomando la dirección correcta en función de la mayor distancia a recorrer.
El código no es infalible ya que como comprabaréis vosotros mismos, no se puede ganar siempre por el mero hecho de la aleatoriedad y de la suerte. Cuando dispongais de un código decente, ejecutarlo varias veces para estar seguros antes de desecharlo.
Curiosidades
Como se suele decir, la banca siempre gana, y en este caso no iba a ser menos y es que en caso de empate ¡la banca gana!
Por último deciros que podéis utilizar el código ya que la web detecta los códigos ganadores para que no se repitan.
AVISO: Debido a que este reto está en activo no publicaré a donde pertenece.
El reto en cuestión nos presenta un esquema de puertas lógicas y una secuencia binaria que al pasarla por las puertas nos devolverá la solución al reto.
Lo primero que necesitamos saber es quefunción realiza cada puerta. Si indagamos un poco enseguida llegamos a la conclusión de que el esquema lo componen 3 puertas NOT, cuatro puertas AND y una puerta OR.
El funcionamiento es muy sencillo, la puerta NOT simplemente invierte el dígito de entrada convirtiendo los unos en ceros y los ceros en unos. La puerta AND siempre dará como resultado cero excepto cuando todos dígitos de entrada sean unos, que dará como resultado uno. La puerta OR es contraria a la AND y siempre dará como resultado uno excepto cuando todos los dígitos de entrada sean ceros, que en este caso dará como resultado cero.
Esquema con apuntes
Nota: Aunque lo más normal es encontrarse puertas de dos entradas y una salida, cuando tenemos múltiples entradas el funcionamiento es el mismo pudiendo resolverlo de manera secuencial. Por ejemplo, a la primera puerta AND le entran la pista cuatro, la dos y la tres. La solución es hacer cuatro AND dos y el resultado AND tres -> (cuatro AND dos) AND tres.
Teniendo en cuenta el funcionamiento de las puertas y con la ayuda del esquema anterior podemos automatizar el proceso fácilmente. A continuación os dejo el código en .Net.
Dim encoded As String = "110111000001110010010011101100011000001101111110000001011101110011101100011000001101011011111000011010100110111000001010100111111111000101110001010"
Dim uno, dos, tres, cuatro, cinco, seis As String
Dim w, x, y, z, tmp As Integer
For i = 0 To encoded.Length - 1 Step 3
uno = Mid(encoded, i + 1, 1)
dos = Mid(encoded, i + 2, 1)
tres = Mid(encoded, i + 3, 1)
If uno = "1" Then cuatro = "0"
If uno = "0" Then cuatro = "1"
If dos = "1" Then cinco = "0"
If dos = "0" Then cinco = "1"
If tres = "1" Then seis = "0"
If tres = "0" Then seis = "1"
w = CInt(cuatro And dos) And CInt(tres)
x = CInt(uno And cinco) And CInt(tres)
y = CInt(uno And dos) And CInt(seis)
z = CInt(uno And dos) And CInt(tres)
tmp = (w Or x) Or (y Or z)
txt_s.Text &= tmp.ToString
Next
Obtenemos como resultado: 1100100110100111001111101001111010011000011101100
Si intentamos decodificar la secuencia resultante en bloque no obtenemos ningún resultado pero si tenemos en cuenta que cada letra en binario ocupa siete dígitos enseguida encontramos la solución.
1100100 1101001 1100111 1101001 1110100 1100001 1101100
d i g i t a l
