Introducción
Este es un crackme de la web de Karpoff programado por Sotanez y realizado en Delphi. Como máximo nos deja meter nombres de 10 dígitos.
El algoritmo
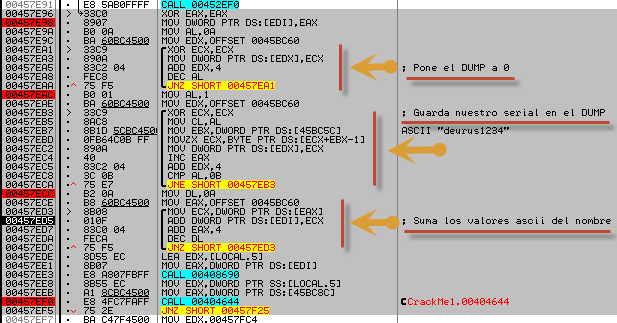
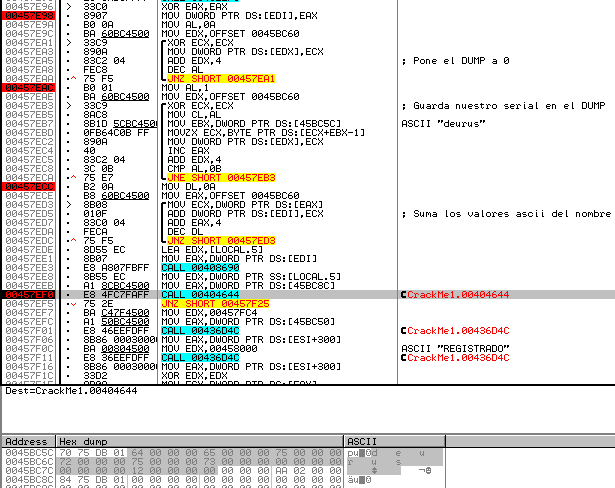
Es un algoritmo muy sencillo pero veremos que nos tendremos que fijar en el DUMP de Olly para saber que demonios hace. Como de costumbre abrimos Olly y en las «Referenced Strings» localizamos la palabra «Registrado«, pinchamos en ella y localizamos la porción de código que nos interesa. Vamos a analizarla.
Vemos 3 bucles, el primero pone la memoria (Dump) a cero, el segundo guarda nuestro nombre (errata en la imagen) en el Dump y el tercero realiza la suma de los valores ascii del nombre. Hasta aquí todo bien, pero vamos a hacer una prueba para el nombre deurus.
- Nombre: deurus
- Serial: 64+65+75+72+75+73 = 298 (664 en decimal)
Probamos el serial en el programa y nos da error, vale, vamos a analizar más a fondo los bucles.
El primer bucle hemos dicho que pone la memoria a 0, en concreto desde «45BC60» y de 4 en 4 (fíjate en el Add 4), es decir, pone a 0 los offsets 45BC60, 45BC64, 45BC68, 45BC6C, 45BC70, 45BC74, 45BC78, 45BC7C, 45BC80, 45BC84, ya que el bucle se repite 10 veces. En la imágen queda claro.
El segundo bucle se repite 11 veces y lo que hace es guardar en el dump el valor ascii de las letras de nuestro nombre. En la imagen lo vemos.
A primera vista ya vemos un valor extraño en la posición 45BC80, y es que cuando debiera haber un 0, hay un 12. Vamos a ver como afecta esto al serial final.
El tercer bucle se repite 10 veces y lo que hace es sumar los valores que haya en el DUMP en las posiciones anteriormente citadas.
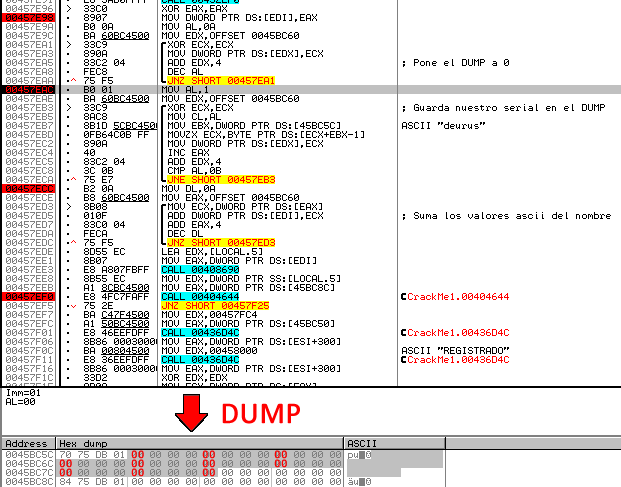
En concreto suma 64+65+75+72+75+73+0+0+12+0 = 2AA (682 en decimal). Probamos 682 como serial y funciona. Realizando más pruebas vemos que para nombres con un tamaño inferior a 5 letras se ocupan las posiciones 45BC70 y 45BC80 con valores extraños, el resto de posiciones se mantienen a 0. En las imágenes inferiores se pueden apreciar más claramente los valores extraños.
Nombre de tamaño < 5.
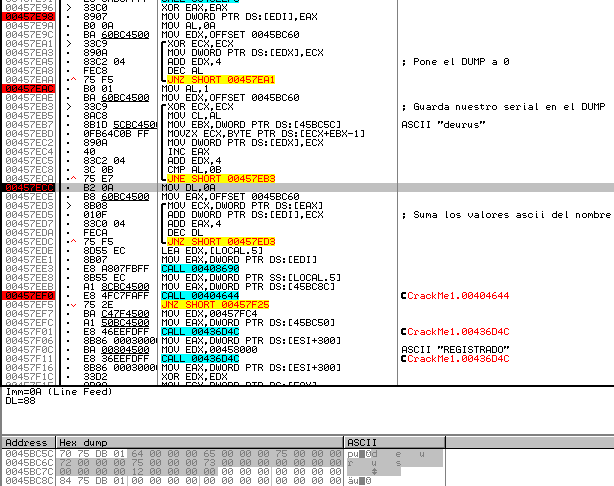
Nombre de tamaño >5 y <9
Nombre de tamaño = 10
En resumen:
Nombre de tamaño < 5 –> Ascii SUM + 14h
Nombre de tamaño >5 y <9 –> Ascii SUM + 12h
Nombre de tamaño =10 –> Ascii SUM
Con esto ya tenemos todo lo que necesitamos para nuestro keygen.
char Nombre[11];
GetWindowText(hwndEdit1, Nombre, 11);
char Serial[20];
int len = strlen(Nombre);
int suma = 0;
for(int i = 0; i <= len; i = i + 1)
{
suma += Nombre[i];
}
if(len < 5){
suma +=0x14;
}
if(len > 5 && len < 9){
suma +=0x12;
}
wsprintf(Serial,"%d",suma);
SetWindowText(hwndEdit2, TEXT(Serial));