Introducción
Este un crackme muy interesante para principiantes ya que la rutina no es muy compleja. Está hecho en ensamblador.
Saltar el antidebug
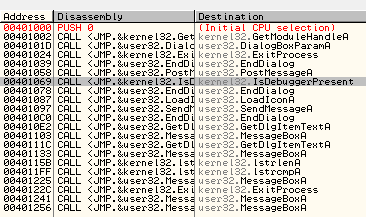
Arrancamos el crackme en Olly damos al play y se cierra. Buscamos en las «Intermodular Calls» y vemos «IsDebuggerPresent«, clickamos sobre ella y vemos el típico call, lo NOPeamos.
Aquí vemos el call.
Call Nopeado.
Encontrando un serial válido
Encontrar en serial válido en esta ocasión es muy sencillo, basta con buscar en las «String References» el mensaje de «Bad boy» y fijarse en la comparación.
El algoritmo
Si nos fijamos en el serial generado nos da muchas pistas pero vamos a destriparlo ya que tampoco tiene mucha complicación. De nuevo miramos en las «String references» y clickamos sobre el mensaje de «bad boy«. Encima de los mensajes vemos claramente la rutina de creación del serial.
004010EB |. 83F8 04 CMP EAX,4 ;Longitud del nombre >4 004010EE |. 72 05 JB SHORT Ice9.004010F5 004010F0 |. 83F8 0A CMP EAX,0A ;Longitud del nombre <=10 004010F3 |. 76 15 JBE SHORT Ice9.0040110A 004010F5 |> 6A 00 PUSH 0 ; /Style = MB_OK|MB_APPLMODAL 004010F7 |. 68 04304000 PUSH Ice9.00403004 ; |Title = "Error, Bad Boy" 004010FC |. 68 1C304000 PUSH Ice9.0040301C ; |Text = "name must be at least 4 chars" 00401101 |. 6A 00 PUSH 0 ; |hOwner = NULL 00401103 |. E8 70010000 CALL <JMP.&user32.MessageBoxA> ; \MessageBoxA ........ 00401183 . 3BD3 CMP EDX,EBX 00401185 . 74 15 JE SHORT Ice9.0040119C 00401187 . 8A07 MOV AL,BYTE PTR DS:[EDI] 00401189 . 3C 5A CMP AL,5A ;Compara que el dígito < 5A 0040118B . 7E 05 JLE SHORT Ice9.00401192 0040118D > 03C8 ADD ECX,EAX ;ECX + Ascii(dígito) 0040118F . 47 INC EDI 00401190 .^ EB EE JMP SHORT Ice9.00401180 00401192 > 3C 41 CMP AL,41 ;Compara que el dígito > 41 00401194 . 7D 02 JGE SHORT Ice9.00401198 00401196 . EB 02 JMP SHORT Ice9.0040119A 00401198 > 04 2C ADD AL,2C ;Si cumple lo anterior dígito +2C 0040119A >^ EB F1 JMP SHORT Ice9.0040118D 0040119C > 81C1 9A020000 ADD ECX,29A ;ECX + 29A 004011A2 . 69C9 39300000 IMUL ECX,ECX,3039 ;ECX * 3039 004011A8 . 83E9 17 SUB ECX,17 ;ECX - 17 004011AB . 6BC9 09 IMUL ECX,ECX,9 ;ECX * 9 004011AE . 33DB XOR EBX,EBX 004011B0 . 8BC1 MOV EAX,ECX ;Mueve nuestro SUM en EAX 004011B2 . B9 0A000000 MOV ECX,0A ;ECX = A 004011B7 > 33D2 XOR EDX,EDX 004011B9 . F7F1 DIV ECX ;SUM / ECX (Resultado a EAX) 004011BB . 80C2 30 ADD DL,30 004011BE . 881433 MOV BYTE PTR DS:[EBX+ESI],DL 004011C1 . 83C3 01 ADD EBX,1 004011C4 . 83F8 00 CMP EAX,0 004011C7 . 74 02 JE SHORT Ice9.004011CB 004011C9 .^ EB EC JMP SHORT Ice9.004011B7 004011CB > BF C8304000 MOV EDI,Ice9.004030C8 004011D0 > 8A4433 FF MOV AL,BYTE PTR DS:[EBX+ESI-1] 004011D4 . 8807 MOV BYTE PTR DS:[EDI],AL 004011D6 . 47 INC EDI 004011D7 . 4B DEC EBX 004011D8 . 83FB 00 CMP EBX,0 004011DB .^ 75 F3 JNZ SHORT Ice9.004011D0 004011DD . C607 00 MOV BYTE PTR DS:[EDI],0 ;Coje letras del nombre en función 004011E0 . 8D3D B4304000 LEA EDI,DWORD PTR DS:[4030B4] ;del resultado anterior 004011E6 . 68 B7304000 PUSH Ice9.004030B7 ; ASCII "rus" 004011EB . 68 C8304000 PUSH Ice9.004030C8 ; ASCII "134992368rus" 004011F0 . E8 BB000000 CALL Ice9.004012B0 ; Concatena 004011F5 . 68 C8304000 PUSH Ice9.004030C8 ; /String2 = "136325628rus" 004011FA . 68 98314000 PUSH Ice9.00403198 ; |String1 = "12345" 004011FF . E8 98000000 CALL <JMP.&kernel32.lstrcmpA> ; \lstrcmpA
Resumen (valores hexadecimales):
- Len(Nombre ) >=4 y <=A
- Comprueba si el dígito está es mayúsculas y si está le sume 2C al valor ascii.
- Suma el valor ascii de todos los dígitos menos el último.
- SUM + 29A
- SUM * 3039
- SUM – 17
- SUM * 9
Finalmente concatena letras siguiendo este criterio:
- Len(nombre) = 4 -> coje la última letra
- Len(nombre) = 5 -> coje las dos últimas
- Len(nombre) = 6 -> coje las tres últimas
- Len(nombre) = 7 -> coje las cuatro últimas
- Len(nombre) = 8 -> coje las cinco últimas
- Len(nombre) = 9 -> coje las seis últimas
- Len(nombre) = A -> coje las siete últimas
Ejemplo para deurus
d e u r u (s) 64+65+75+72+75 = 225 225 + 29A = 4BF 4BF * 3039 = E4DE87 E4DE87 - 17 = E4DE70 E4DE70 * 9 = 80BD1F0 ;Pasamos a decimal y concatenamos 134992368rus
Ejemplo para Deurus
D e u r u (s) 44(+2C)+65+75+72+75 = 25D 25D + 29A = 4F7 4BF * 3039 = EF6AFF EF6AFF - 17 = EF6AE8 EF6AE8 * 9 = 86AC228 ;Pasamos a decimal y concatenamos 141214248rus
Como curiosidad decirtos que con el tiempo valores del estilo 29A y 3039 os pegarán rápido al ojo ya que equivalen a 666 y 12345 en decimal. Por cierto 29A fue un grupo de hackers creadores de virus muy conocido en la escena Nacional e Internacional.