por ·Sin comentarios

Introducción

Esta vez se trata de un crackme realizado en VC++ 5.0/6.0 y en sus entrañas utiliza RSA-24. En este caso la peculiaridad es que el nombre no interviene en la generación del serial siendo un resultado único.

Resumen RSA

Parámetros

p = Primer número primo
q = Segundo número primo
e = Exponente público que cumpla MCD(e,(p-1)*(q-1))==1
n = Módulo público siendo n=p*q
d = Exponente privado que cumpla d=e^(-1) mod ((p-1)*(q-1))

De este modo e y n son la parte pública de la clave y d y n la parte privada. Los número primos p y q se utilizan solo para generar los parámetros y de ahí en adelante se pueden desechar.

Funciones de Cifrado/Descifrado

cifrado = descifrado ^ e mod n
descifrado = cifrado ^ d mod n

OllyDbg

Nuestro primer vistazo con OllyDbg nos muestra cuatro números de los que podemos hacernos una idea de que 9901 es un buen candidato a ser el exponente público (e) y 12790891 el módulo n ya que casualmente es un número de 24 bits. Los otros dos números de momento no nos dicen nada.

Referencias de texto

A continuación de los números tenemos la rutina de comprobación en la que comprueba que nuestro serial tenga 14 dígitos y lo divide en dos partes de 7 dígitos. Interesante ya que los otros dos números que aparecían en las referencias de texto tienen 7 dígitos cada uno.

004029CD  |.  68 DC004200   PUSH    RSA24.004200DC                         ;  ASCII "9901"
004029D2  |.  8D8C24 E40000>LEA     ECX,[DWORD SS:ESP+E4]
004029D9  |.  E8 52E7FFFF   CALL    RSA24.00401130
004029DE  |.  68 D0004200   PUSH    RSA24.004200D0                         ;  ASCII "12790891"
004029E3  |.  8D4C24 1C     LEA     ECX,[DWORD SS:ESP+1C]
004029E7  |.  C78424 640600>MOV     [DWORD SS:ESP+664],0
004029F2  |.  E8 39E7FFFF   CALL    RSA24.00401130
004029F7  |.  68 C8004200   PUSH    RSA24.004200C8                         ;  ASCII "8483678"
004029FC  |.  8D8C24 740200>LEA     ECX,[DWORD SS:ESP+274]
00402A03  |.  C68424 640600>MOV     [BYTE SS:ESP+664],1
00402A0B  |.  E8 20E7FFFF   CALL    RSA24.00401130
00402A10  |.  68 C0004200   PUSH    RSA24.004200C0                         ;  ASCII "5666933"
00402A15  |.  8D8C24 AC0100>LEA     ECX,[DWORD SS:ESP+1AC]
00402A1C  |.  C68424 640600>MOV     [BYTE SS:ESP+664],2
00402A24  |.  E8 07E7FFFF   CALL    RSA24.00401130
00402A29  |.  8B9424 680600>MOV     EDX,[DWORD SS:ESP+668]
00402A30  |.  83CE FF       OR      ESI,FFFFFFFF
00402A33  |.  8BFA          MOV     EDI,EDX
00402A35  |.  8BCE          MOV     ECX,ESI
00402A37  |.  33C0          XOR     EAX,EAX
00402A39  |.  C68424 600600>MOV     [BYTE SS:ESP+660],3
00402A41  |.  F2:AE         REPNE   SCAS [BYTE ES:EDI]
00402A43  |.  F7D1          NOT     ECX
00402A45  |.  49            DEC     ECX
00402A46  |.  83F9 0E       CMP     ECX,0E                                 ;  serial 0xE chars -> 14 digitos
00402A49  |.  0F85 63010000 JNZ     RSA24.00402BB2
00402A4F  |.  33C9          XOR     ECX,ECX
00402A51  |>  8A0411        /MOV     AL,[BYTE DS:ECX+EDX]                  ;  {
00402A54  |.  3C 30         |CMP     AL,30
00402A56  |.  0F8C 56010000 |JL      RSA24.00402BB2
00402A5C  |.  3C 39         |CMP     AL,39                                 ;  comprueba que el serial sea numerico
00402A5E  |.  0F8F 4E010000 |JG      RSA24.00402BB2
00402A64  |.  41            |INC     ECX
00402A65  |.  83F9 0E       |CMP     ECX,0E
00402A68  |.^ 7C E7         \JL      SHORT RSA24.00402A51                  ;  }
00402A6A  |.  8BC2          MOV     EAX,EDX
00402A6C  |.  C64424 17 00  MOV     [BYTE SS:ESP+17],0                     ;  {
00402A71  |.  C64424 0F 00  MOV     [BYTE SS:ESP+F],0
00402A76  |.  8B08          MOV     ECX,[DWORD DS:EAX]
00402A78  |.  894C24 10     MOV     [DWORD SS:ESP+10],ECX
00402A7C  |.  66:8B48 04    MOV     CX,[WORD DS:EAX+4]
00402A80  |.  66:894C24 14  MOV     [WORD SS:ESP+14],CX
00402A85  |.  8B4A 07       MOV     ECX,[DWORD DS:EDX+7]
00402A88  |.  8A40 06       MOV     AL,[BYTE DS:EAX+6]                     ;  divide el serial en dos partes de 7 digitos
00402A8B  |.  894C24 08     MOV     [DWORD SS:ESP+8],ECX
00402A8F  |.  884424 16     MOV     [BYTE SS:ESP+16],AL
00402A93  |.  8D42 07       LEA     EAX,[DWORD DS:EDX+7]
00402A96  |.  8D4C24 10     LEA     ECX,[DWORD SS:ESP+10]
00402A9A  |.  66:8B50 04    MOV     DX,[WORD DS:EAX+4]
00402A9E  |.  8A40 06       MOV     AL,[BYTE DS:EAX+6]                     ;  }

A continuación hace una serie de operaciones matemáticas para finalmente comparar el resultado con 8483678 y con 5666933. Lo que está haciendo es cifrar con nuestro serial en dos partes para comprobar que tenemos el número descifrado. Veamos un ejemplo con el serial 12345678901234.

descifrado ^ e mod n = cifrado
x1 = 1234567 y x2 = 8901234
1º parte del serial
x1 ^ 9901 mod 12790891 != 8483678
2º parte del serial
x2 ^ 9901 mod 12790891 != 5666933

Obviamente el resultado de las operaciones anteriores no da ese resultado y el Crackme nos tira fuera de modo que no nos queda más que atacar a RSA para obtener los primos p y q y el módulo privado d. De este modo podremos obtener los números buenos.

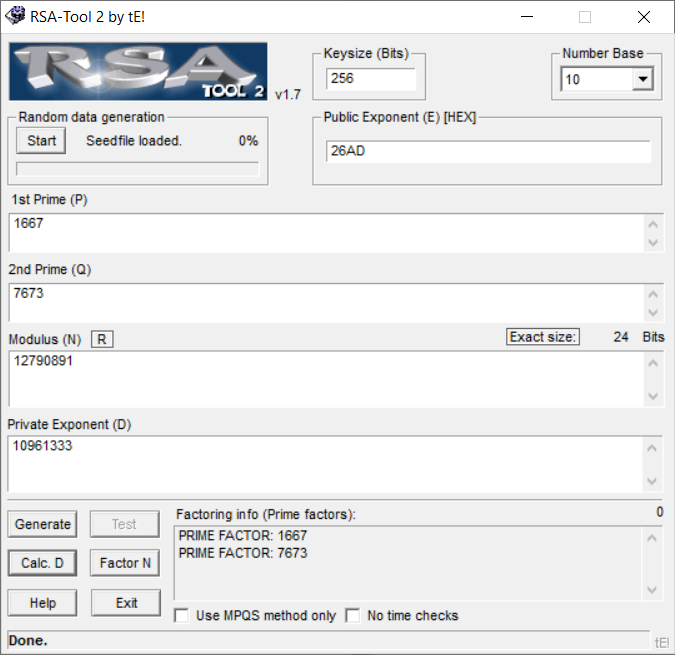
Los primos p y q se obtienen factorizando (botón Factor N) y una vez que tenemos p y q hallamos d (botón Calc. D). Todo esto es coser y cantar con la ayuda de la herramienta RSA-Tool 2. El exponente público e se introduce en hexadecimal.

Obteniendo p, q y d

Una vez que tenemos d hallamos el serial de forma sencilla con la herramienta Big Integer Calculator.

cifrado ^ d mod n = descifrado
1º parte del serial
8483678 ^ 10961333 mod 12790891 = 7167622
2º parte del serial
5666933 ^ 10961333 mod 12790891 = 3196885

SERIAL = 71676223196885
1º parte del serial
2º parte del serial

Enlaces