Keygen para el Crackme Sweeet Dream 1.0 de 2Sweeet

por ·Sin comentarios

Intro

Hoy tenemos aquí un crackme del año 2000 empacado y con un algoritmo aunque no muy complicado largo de tracear. Está empacado varias veces, algo poco habitual pero recordemos que es un crackme antiguo. Tras el empacado se encuentra Delphi.

Herramientas

  • PEiD o similar.
  • OllyDbg con plugin OllyDumpEX.
  • Import REConstructor.
  • LordPE (Opcional).

Desempacado multicapa

VideoTutorial del desempacado disponible

Si lo pasamos por PEiD nos dice que Aspack 2.1, Exeinfo no está muy seguro y RDG packer detector en el escaneo avanzado nos encuentra Aspack, UPX y PE-Pack.

En principio nos enfrentamos a Aspack 2.1, abrimos el crackme con OllyDbg y vemos el típico PUSHAD.

01

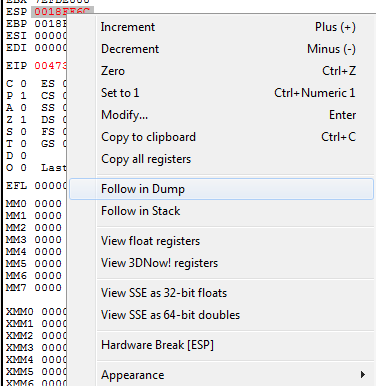
Pulsamos F8 (Step Over) y a continuación click derecho sobre el registro ESP y Follow in DUMP.

02

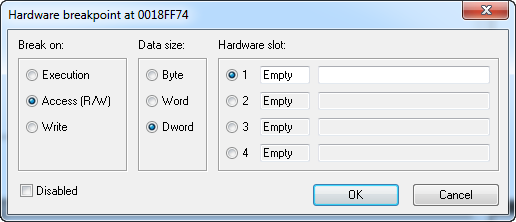
Seleccionamos los primeros cuatro bytes útiles del dump y les ponemos un Breakpoint de Hardware, Access y Dword.

04

05

Pulsamos F9 y nos para aquí:

06

Ya tenemos a Aspack contra las cuerdas, pulsamos F8 hasta después del RETN para llegar al OEP (Original Entry Point).

07

Pero en el supuesto OEP vemos otro PUSHAD por lo que esto no ha terminado. Investigando un poco más vemos que la segunda capa se corresponde con PE-PACK 1.0. La estrategia a seguir es la misma, como ya tenemos el breakpoint puesto pulsamos F9 y nos para aquí:

08

Pulsamos F8 y nos llega a otro PUSHAD. Esta vez es UPX.

09

Pulsamos de nuevo F9 y paramos aquí:

10

Pulsamos F8 y esta vez si llegamos al OEP (4576EC).

11

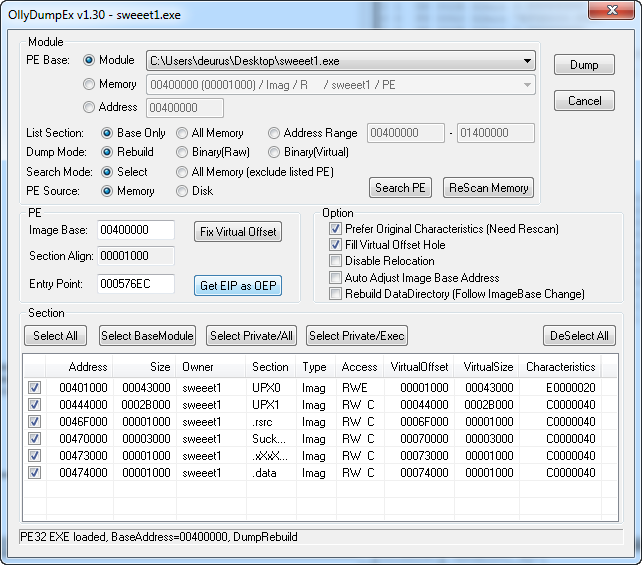
A continuación vamos a dumpear el archivo en memoria. Vamos a plugins > OllyDumpEX, pulsamos sobre «Get EIP as OEP» y finalmente sobre «Dump«.

13

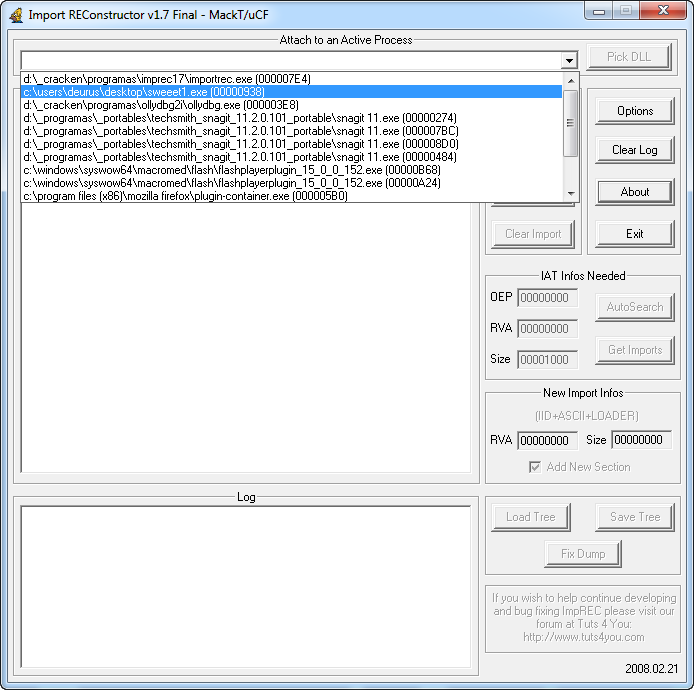
Minimizamos Olly (no cerrar), abrimos el programa ImportREC y seleccionamos el ejecutable «Sweeet1.exe».

14

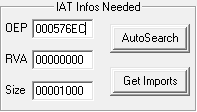
Pegamos el OEP original (576EC), le damos a AutoSearch y a continuación a Get Imports.

15

Finalmente pulsamos Fix Dump y elegimos el ejecutable dumpeado anteriormente. Esto nos genera un ejecutable dumpeado que es el ejecutable válido.

Ahora PEiD nos dice que estamos tratando con un crackme hecho en Delphi.

Hemos pasado por tres capas de compresión casi idénticas, vamos a analizarlas.

triplecompresion

El algoritmo

Cuando abrimos el crackme nos fijamos en que genera una key. Esta key se genera en función del disco duro desde el que se ejecuta.

Como la secuencia de generación del serial válido es larga os pongo lo más importante muy resumido y con ejemplos como siempre.

El serial es del siguiente tipo:

Serial = 1ªParte-2ªParte-3ªParte
Serial = 0000XXXXX-SerialCalculado-xxxx000Z8

Comprobación del tamaño del nombre
----------------------------------
........
00456EAA    E8 01CCFAFF     CALL sweeet1_Fix_dump_rebuilded.00403AB0
00456EAF    83F8 04         CMP EAX,4    ------------------------------------------------; Nombre >=4                    
00456EB2    7D 13           JGE SHORT sweeet1_Fix_dump_rebuilded.00456EC7
00456EB4    A1 08954500     MOV EAX,DWORD PTR DS:[sweeet1_Fix_dump_rebuilded.459508]
00456EB9    8B00            MOV EAX,DWORD PTR DS:[EAX]
00456EBB    E8 0869FEFF     CALL sweeet1_Fix_dump_rebuilded.0043D7C8
00456EC0    BB 01000000     MOV EBX,1
00456EC5    EB 15           JMP SHORT sweeet1_Fix_dump_rebuilded.00456EDC
00456EC7    83FB 25         CMP EBX,25                                                                                                
00456ECA    7D 0E           JGE SHORT sweeet1_Fix_dump_rebuilded.00456EDA
00456ECC    83C3 32         ADD EBX,32
00456ECF    83C3 1E         ADD EBX,1E
00456ED2    83EB 4F         SUB EBX,4F
00456ED5    83FB 25         CMP EBX,25 -----------------------------------------------; Nombre <=25
00456ED8  ^ 7C F2           JL SHORT sweeet1_Fix_dump_rebuilded.00456ECC
00456EDA    33DB            XOR EBX,EBX
00456EDC    33C0            XOR EAX,EAX
........

1ºBucle - Nuestro nombre (A)
----------------------------
........
00456F55    BE 1B000000     MOV ESI,1B -------------------------------; ESI = 1B
00456F5A    EB 21           JMP SHORT sweeet1_dump_.00456F7D
00456F5C    8D55 D4         LEA EDX,[EBP-2C]
00456F5F    A1 34A84500     MOV EAX,DWORD PTR DS:[sweeet1_dump_.45A8
00456F64    8B80 C4020000   MOV EAX,DWORD PTR DS:[EAX+2C4]
00456F6A    E8 B5DAFCFF     CALL sweeet1_dump_.00424A24
00456F6F    8B45 D4         MOV EAX,DWORD PTR SS:[EBP-2C]
00456F72    0FB64418 FF     MOVZX EAX,BYTE PTR DS:[EBX+EAX-1]---------; Coje digito
00456F77    03F0            ADD ESI,EAX ------------------------------; digito + ESI
00456F79    43              INC EBX
00456F7A    0FAFF3          IMUL ESI,EBX  ----------------------------; multiplica por i (bucle)
00456F7D    8D55 D4         LEA EDX,[EBP-2C]
........

2ºBucle - La key (B)
--------------------
........
00456F9C         |.  BF 1A000000            MOV EDI,1A -------------------------;EDI = 1A
00456FA1         |.  BB 01000000            MOV EBX,1
00456FA6         |.  EB 1E                  JMP SHORT sweeet1_.00456FC6
00456FA8         |>  8D55 D4                /LEA EDX,[LOCAL.11]
00456FAB         |.  A1 34A84500            |MOV EAX,DWORD PTR DS:[45A834]
00456FB0         |.  8B80 D0020000          |MOV EAX,DWORD PTR DS:[EAX+2D0]
00456FB6         |.  E8 69DAFCFF            |CALL sweeet1_.00424A24
00456FBB         |.  8B45 D4                |MOV EAX,[LOCAL.11]
00456FBE         |.  0FB64418 FF            |MOVZX EAX,BYTE PTR DS:[EAX+EBX-1]--;Coje dígito
00456FC3         |.  03F8                   |ADD EDI,EAX -----------------------;Suma dígito a dígito
00456FC5         |.  43                     |INC EBX
00456FC6         |>  8D55 D4                 LEA EDX,[LOCAL.11]
00456FC9         |.  A1 34A84500            |MOV EAX,DWORD PTR DS:[45A834]
00456FCE         |.  8B80 D0020000          |MOV EAX,DWORD PTR DS:[EAX+2D0]
00456FD4         |.  E8 4BDAFCFF            |CALL sweeet1_.00424A24
00456FD9         |.  8B45 D4                |MOV EAX,[LOCAL.11]
00456FDC         |.  E8 CFCAFAFF            |CALL sweeet1_.00403AB0
00456FE1         |.  3BD8                   |CMP EBX,EAX
00456FE3         |.^ 7C C3                  \JL SHORT sweeet1_.00456FA8
........

Generación del serial central
-----------------------------
........
00456FE5         |.  B9 01000000            MOV ECX,1
00456FEA         |.  BB 01000000            MOV EBX,1
00456FEF         |.  8BC7                   MOV EAX,EDI
00456FF1         |.  F7EE                   IMUL ESI ----------; C = A * B
00456FF3         |.  99                     CDQ
........
00456FFD         |.  2345 E8                AND EAX,[LOCAL.6]--; D = A and C
00457000         |.  2355 EC                AND EDX,[LOCAL.5]
00457003         |.  8945 E8                MOV [LOCAL.6],EAX
00457006         |.  8955 EC                MOV [LOCAL.5],EDX
........
00457032         |.  8BC7                   MOV EAX,EDI
00457034         |.  99                     CDQ
00457035         |.  0345 E8                ADD EAX,[LOCAL.6]--; E = D + B
00457038         |.  1355 EC                ADC EDX,[LOCAL.5]
0045703B         |.  8945 E0                MOV [LOCAL.8],EAX
0045703E         |.  8955 E4                MOV [LOCAL.7],EDX
........
00405732           8B4424 10                MOV EAX,DWORD PTR SS:[ESP+10]
00405736           F72424                   MUL DWORD PTR SS:[ESP]
00405739           8BC8                     MOV ECX,EAX
0040573B           8B4424 04                MOV EAX,DWORD PTR SS:[ESP+4]
0040573F           F76424 0C                MUL DWORD PTR SS:[ESP+C]------; F = B * D
00405743           03C8                     ADD ECX,EAX
00405745           8B0424                   MOV EAX,DWORD PTR SS:[ESP]
00405748           F76424 0C                MUL DWORD PTR SS:[ESP+C]------; G = A * F
........
0045705E         |.  0B0424                 OR EAX,DWORD PTR SS:[ESP]-----; Serial central = G or A
........
00457077         |.  E8 FC07FBFF            CALL sweeet1_.00407878
0045707C         |.  8B45 F8                MOV EAX,[LOCAL.2]-------------; EAX = Serial central
........
004570D1         |.  E8 A207FBFF            CALL sweeet1_.00407878
004570D6         |.  8B45 D0                MOV EAX,[LOCAL.12]
004570D9         |.  E8 D2C9FAFF            CALL sweeet1_.00403AB0--------; Obtiene longitud del serial central en hexa
004570DE         |.  8BD8                   MOV EBX,EAX
........
004570D1         |.  E8 A207FBFF            CALL sweeet1_.00407878--------;*Nota

*Nota:
A partir de aquí genera la primera y tercera parte del serial de la siguiente manera:

Serial = 1ªParte-2ªParte-3ªParte
Serial = 0000XXXXX-SerialCalculado-xxxx000Z8

1ºParte = 3ºdigSerial+1ºdigSerial+2ºdigSerial+3ºdigSerial+4ºdigNombreMayu+2ºdigNombreMayu+5ºdigNombreMayu+1ºdigNombreMayu+3ºdigNombreMayu
3ºParte = 3ºdigNombreMin+1ºdigNombreMin+4ºdigNombreMin+2ºdigNombreMin+Tamaño Serial_2ªParte en Hex y de tres dígitos+Z8

 Ejemplo:

Nombre: deurus
Key:    C0C0A000
Serial: 6906REUDU-906297047918-udre00CZ8

1) A = 23A2A (Con nuestro nombre empezando por 1B se lo suma a ESI y se lo multiplica por i (la que toque cada vez))
2) B = 1A1 (Con nuestra Key empezando por 1A va sumando los digitos)
3) C = B * A = 3A0BE6A
4) D = A and C = 3A2A
5) E = D + B = 3BCB (Offset 457035)
6) F = B * D = 5EBE6A (Offset 48704A)
7) G = A * F = D303834164
8) Serial = G or A (Serial = D303834164 or 23A2A = D303837B6E (906297047918))

 A tener en cuenta:

  • 1ªParte del serial siempre mayúsculas.
  • 2ªParte siempre numérico. Usa el registro de 64 bits (Qword) con signo.**Nota
  • 3ªParte siempre minúsculas.

**Nota:

Nombre: deurus.info
Key:    E09FF000
Serial: 9169REUDU-16918236-udre008Z8

Fíjate que: -16918236 = FFFFFFFFFEFDD924

Nombre: deurus
Key:    C0C0A000
Serial: 6906REUDU-906297047918-udre00CZ8

906297047918 = 000000D303837B6E

Links

Blooper Tech Movie XII – Enemigo público
Sinopsis Enemigo público (Enemy of the State) es una película de acción y suspense dirigida por Tony Scott, estrenada en
Solución al CrackMe Matrix de ZemoZ
Introducción Aquí tenemos un CrackMe diferente a lo que estamos acostumbrados, ya que en vez del típico número de serie
Keygen para el CrackMe Pythagoras de Spider
Introducción Hoy tenemos aquí un bonito crackme matemático realizado por Spider. El crackme está realizado en ensamblador y precisamente por
ChatGPT vs CTF matemático
El reto Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero

Blooper Tech Movie XII – Enemigo público

por ·Sin comentarios

Sinopsis

Enemigo público (Enemy of the State) es una película de acción y suspense dirigida por Tony Scott, estrenada en 1998. La historia sigue a Robert Clayton Dean (Will Smith), un abogado de Washington D.C. que se ve atrapado en una conspiración de vigilancia masiva cuando recibe, sin saberlo, una cinta de video que documenta el asesinato de un congresista a manos de un alto funcionario de la Agencia de Seguridad Nacional (NSA), interpretado por Jon Voight. La situación se complica cuando la NSA utiliza toda su tecnología de espionaje para seguir y neutralizar a Dean.

Dean encuentra ayuda en Edward «Brill» Lyle (Gene Hackman), un exanalista de la NSA convertido en un experto en vigilancia que vive en el anonimato. Juntos intentan descubrir la verdad y exponer la conspiración, mientras son perseguidos por la propia NSA. Un papel crucial también lo desempeña el personaje de Daniel Zavitz, interpretado por Jason Lee, un joven investigador que graba accidentalmente el asesinato y termina transmitiendo la evidencia a Dean. El elenco incluye además a Lisa Bonet, Regina King, Jack Black, Barry Pepper, y Seth Green.

Tecnología utilizada

En Enemigo Público, la tecnología juega un papel crucial no solo en la trama sino también en la ambientación de la película. La precisión y el realismo de los equipos informáticos utilizados contribuyen a la atmósfera de paranoia y vigilancia que define la narrativa.

El PC de Daniel Zavitz (Jason Lee)

Jason Lee, en su papel de Daniel Zavitz, utiliza un PC clónico, claramente identificado por el logo de Sun Microsystems en la torre del ordenador. Sin embargo, el sistema operativo que corre en esta máquina es Windows 3.1, una versión que, para 1998, ya estaba obsoleta, habiendo sido lanzada en 1992. Esta elección subraya el hecho de que Zavitz utiliza equipamiento más económico y anticuado, en contraste con la tecnología más avanzada de otros personajes.

Zavitz también utiliza Media Player, un reproductor de video básico integrado en Windows 3.1. Durante la reproducción del archivo de video crucial para la trama, se puede observar que la extensión del archivo es .CAM. Este tipo de archivo podría implicar un video capturado por una cámara, pero también sugiere (por otros fotogramas de la película) que el codec utilizado para comprimir el video podría ser QuickTime, permitiendo una reproducción cruzada entre diferentes sistemas operativos.

Además, Zavitz utiliza un reproductor portátil NEC Turbo Express, un dispositivo de videojuegos portátil de la época. En la película, este dispositivo es empleado de manera innovadora para reproducir y transferir datos, algo poco realista pero que añade dramatismo a la escena. La tarjeta PCMCIA de 200MB que Zavitz utiliza para almacenar el video es otro ejemplo de la tecnología de la época, reflejando la capacidad de almacenamiento portátil antes de la popularización de los dispositivos USB.

El Equipo de Edward «Brill» Lyle (Gene Hackman)

Por su parte, Gene Hackman, en su papel de Brill, maneja un sistema considerablemente más avanzado, utilizando Windows 98. Este sistema operativo, lanzado también en 1998, representaba lo más avanzado en términos de compatibilidad y usabilidad en ese momento, lo que refuerza la imagen de Brill como un experto en tecnología con acceso a mejores recursos.

Aunque en la película no se detalla el hardware específico de Brill, el hecho de que use Windows 98, junto con las capacidades de manipulación y decodificación de video que se muestran, sugiere que tiene acceso a tecnología de alta gama para la época. En una escena clave, se observa cómo Brill decodifica el video utilizando una interfaz gráfica llamativa, diseñada claramente para atraer la atención del espectador, más que para reflejar la realidad de la tecnología disponible en ese momento.

Conclusión

La producción de Enemigo Público es destacable por su atención al detalle en lo referente al equipamiento tecnológico de los personajes. El contraste entre el equipo más antiguo y económico utilizado por Daniel Zavitz (Jason Lee) y el sistema más avanzado de Edward Lyle (Gene Hackman) refleja de manera efectiva el trasfondo de los personajes. Zavitz, como investigador freelance, se maneja con recursos limitados, mientras que Lyle, con su pasado en la NSA y mayor poder adquisitivo, tiene acceso a tecnología más avanzada.

Otro detalle interesante es la diferenciación en el equipamiento dentro de la central de la NSA. Mientras los empleados comunes utilizan monitores CRT, que eran estándar en la época, el personaje de Thomas Reynolds (Jon Voight) dispone de una pantalla plana, lo que subraya su estatus superior dentro de la agencia. Estos detalles de producción contribuyen a la autenticidad y la profundidad visual de la película.

Sin embargo, la película no está exenta de licencias creativas que sacrifican el realismo tecnológico en favor del impacto visual. Un ejemplo claro es cuando un técnico de la NSA, a partir de un fotograma de un vídeo de seguridad, rota la imagen en 3D para simular lo que Zavitz podría haber introducido en la bolsa de Dean. Aunque esta secuencia añade dramatismo, carece de una base tecnológica realista.

Del mismo modo, la escena donde Brill decodifica el vídeo utilizando una interfaz visualmente llamativa es un claro ejemplo de cómo la película opta por elementos más glamurosos para captar la atención del espectador, alejándose de la realidad técnica, donde estos procesos serían mucho menos espectaculares y más funcionales. Además se pueden observar las siguientes curiosidades:

  • Se ve el escritorio de Windows 98 con fondo negro y tres aplicaciones abiertas, QuickTime for Windows, una carpeta y una imagen.
  • Una carpeta abierta con cuatro archivos DIR y nombres que nos hacen creer que uno está encriptado y otro no. Dos archivos de imagen con extensión TIF y dos archivos de vídeo con extensión MOV. Ojo porque DIR es la extensión de proyectos de Adobe Director, ahí lo dejo.
  • La animación muestra el 100% antes que la barra de progreso llegue al final.
  • Una vez decodificado se nos muestra el vídeo pero como se nos mostró anteriormente con el media player de Windows 3.1. Incluso se ve el icono de minimizar típico de Windows 3.1 en la parte superior izquierda (última imagen).

En resumen, Enemigo Público logra un equilibrio eficaz entre el realismo tecnológico y las exigencias dramáticas del cine. A pesar de algunas exageraciones en la representación de la tecnología, la atención al detalle en los aspectos técnicos y la diferenciación de equipos según los personajes y sus circunstancias es un testimonio del buen trabajo de producción que hace que la película siga siendo entretenida, incluso más de dos décadas después de su estreno.

Solución al CrackMe Matrix de ZemoZ

por ·Sin comentarios

Introducción

Aquí tenemos un CrackMe diferente a lo que estamos acostumbrados, ya que en vez del típico número de serie asociado a un nombre la comprobación se realiza mediante checkboxes con una matriz de 7×3. El CrackMe está realizado en Visual C++ lo que facilita en parte encontrar rápidamente la rutina de comprobación.

Comprobación

004013C5   > /8B7424 10     MOV     ESI,[DWORD SS:ESP+10]						;
004013C9   . |33FF          XOR     EDI,EDI
004013CB   > |8B86 74304000 MOV     EAX,[DWORD DS:ESI+403074]                   ;
004013D1   . |8BCB          MOV     ECX,EBX
004013D3   . |50            PUSH    EAX
004013D4   . |E8 6F020000   CALL    <JMP.&MFC42.#3092_CWnd::GetDlgItem>			; Lee el estado del checkbox
004013D9   . |8B48 20       MOV     ECX,[DWORD DS:EAX+20]
004013DC   . |6A 00         PUSH    0
004013DE   . |6A 00         PUSH    0
004013E0   . |68 F0000000   PUSH    0F0
004013E5   . |51            PUSH    ECX                                         ; 
004013E6   . |FFD5          CALL    NEAR EBP
004013E8   . |3B86 20304000 CMP     EAX,[DWORD DS:ESI+403020]					; Comprueba el estado del checkbox (1 activado 0 desactivado)
004013EE   . |75 20         JNZ     SHORT Matrix_C.00401410						; Salto a chico malo
004013F0   . |47            INC     EDI											; Incrementa contador
004013F1   . |83C6 04       ADD     ESI,4
004013F4   . |83FF 07       CMP     EDI,7										; ¿Hemos terminado de leer las columnas? ¿contador = 7?
004013F7   .^|7C D2         JL      SHORT Matrix_C.004013CB                     ; si terminan las columnas deja pasar
004013F9   . |8B4424 10     MOV     EAX,[DWORD SS:ESP+10]
004013FD   . |83C0 1C       ADD     EAX,1C										; contador de filas
00401400   . |83F8 54       CMP     EAX,54										; 3 filas = 1C+1C+1C=54
00401403   . |894424 10     MOV     [DWORD SS:ESP+10],EAX
00401407   .^\7C BC         JL      SHORT Matrix_C.004013C5						; ¿Hemos terminado de leer la fila? ¿contador = 54?
00401409   .  68 D8304000   PUSH    Matrix_C.004030D8                           ;  ASCII "Registration successful!"
0040140E   .  EB 05         JMP     SHORT Matrix_C.00401415
00401410   >  68 C8304000   PUSH    Matrix_C.004030C8                           ;  ASCII "Not registered!"

En la rutina de comprobación se ve fácil un CMP EDI,7 por lo que podemos deducir que si el creador no se ha molestado mucho la comprobación se realiza de izquierda a derecha y de arriba hacia abajo.

Orden de comprobación

Tal es así que si ponemos un breakpoint en 4013E8, podemos ir sacando el estado correcto de los checkboxes sin mucha molestia.

Resultado final

Enlaces

Keygen para el CrackMe Pythagoras de Spider

por ·Sin comentarios

Introducción

Hoy tenemos aquí un bonito crackme matemático realizado por Spider. El crackme está realizado en ensamblador y precisamente por eso, vamos a tener que lidiar con ciertas peculiaridades al realizar el keygen con un lenguaje de bajo nivel.

Al inicio comprueba la longitud del nombre y de el número de serie. El nombre debe tener al menos 6 caracteres y el número de serie debe tener 10. Os adelanto ya que la asignación de memoria del nombre es de 9 caracteres, es decir, da igual la longitud del nombre que solo va a usar 9.

004014AD | E8 1A 02 00 00           | call <pythagoras.GetWindowTextA>        | ;Lee el nombre
004014B2 | 83 F8 06                 | cmp eax,6                               | ;Nombre >=6 caracteres
004014B5 | 0F 82 03 01 00 00        | jb pythagoras.4015BE                    |
004014BB | 6A 14                    | push 14                                 |
004014BD | 68 D9 31 40 00           | push pythagoras.4031D9                  | ;004031D9:"1234567890"
004014C2 | FF 35 10 32 40 00        | push dword ptr ds:[403210]              |
004014C8 | E8 FF 01 00 00           | call <pythagoras.GetWindowTextA>        | ;Lee el serial
004014CD | 83 F8 0A                 | cmp eax,A                               | ;Serial debe tener 10 (A) caracteres
004014D0 | 0F 85 E8 00 00 00        | jne pythagoras.4015BE                   |

Sabiendo esto introducimos Nombre: deurus y Serial: 1234567890

A continuación chequea que nuestro serial tenga caracteres hexadecimales.

004014DA | 8A 81 D9 31 40 00        | mov al,byte ptr ds:[ecx+4031D9]         | ; ecx+004031D9:"1234567890"
004014E0 | 3C 00                    | cmp al,0                                | ; contador del bucle
004014E2 | 74 1F                    | je pythagoras.401503                    | ; fin del bucle
004014E4 | 3C 30                    | cmp al,30                               | ; 0x30 = número 1
004014E6 | 0F 82 D2 00 00 00        | jb pythagoras.4015BE                    | ; < 30 bad boy
004014EC | 3C 46                    | cmp al,46                               | ; 0x46 = letra F
004014EE | 0F 87 CA 00 00 00        | ja pythagoras.4015BE                    | ; > 46 bad boy
004014F4 | 3C 39                    | cmp al,39                               | ; 0x39 = número 9
004014F6 | 76 08                    | jbe pythagoras.401500                   | ; <=39 ok continua el bucle
004014F8 | 3C 41                    | cmp al,41                               | ; 0x41 = letra A
004014FA | 0F 82 BE 00 00 00        | jb pythagoras.4015BE                    | ; <41 bad boy
00401500 | 41                       | inc ecx                                 | ; contador += 1
00401501 | EB D7                    | jmp pythagoras.4014DA                   | ; bucle

Continua realizando un sumatorio con nuestro nombre, pero tenemos que tener especial cuidado al tratamiento de los datos, ya que el crackme al estar hecho en ensamblador puede jugar con los registros como quiere y eso nos puede inducir a error.

0040150B | 3C 00                    | cmp al,0                                | ; ¿Fin bucle?
0040150D | 74 05                    | je pythagoras.401514                    | ; Salta fuera del bucle si procede
0040150F | 02 D8                    | add bl,al                               | ; bl = bl + al
00401511 | 41                       | inc ecx                                 | ; contador +=1
00401512 | EB F1                    | jmp pythagoras.401505                   | ; bucle

Si os fijáis utiliza registros de 8 bits como son AL y BL. Debajo os dejo una explicación de EAX pero para EBX es lo mismo.

               EAX
-----------------------------------
                         AX
                  -----------------
                     AH       AL
                  -------- --------
00000000 00000000 00000000 00000000
 (8bit)   (8bit)   (8bit)   (8bit)
 

  EAX     (32 bit)
--------
     AX   (16 bit)
    ----
    AHAL  (AH y AL 8 bit)
--------
00000000

El uso de registros de 8 bits nos implica tomar precauciones al realizar el Keygen debido a que por ejemplo, en .Net no tenemos la capacidad de decirle que haga una suma y que nos devuelva solamente 8 bits del resultado. Veamos como ejemplo para el nombre «deurus». La suma de los caracteres hexadecimales quedaría:

64+65+75+72+75+73 = 298, es decir, EAX = 00000298

Pero recordad que el crackme solo cogerá el 98 que es lo correspondiente al registro AL. De momento nos quedamos con nuestro SUMNOMBRE = 98.

Primera condición

A continuación coge los dos primeros caracteres del serial y les resta nuestro SUMNOMBRE y comprueba que el resultado esté entre 4 (0x4) y -4 (0xFC).

0040154B | 0F B6 05 F3 31 40 00     | movzx eax,byte ptr ds:[4031F3]          |
00401552 | 8A C8                    | mov cl,al                               |
00401554 | 2A CB                    | sub cl,bl                               | ; CL = CL - BL | CL = 12 - 98 = 7A
00401556 | 80 F9 04                 | cmp cl,4                                | ; Compara CL con 4
00401559 | 7F 63                    | jg pythagoras.4015BE                    | ; Salta si es mayor
0040155B | 80 F9 FC                 | cmp cl,FC                               | ; Compara CL con FC (-4)
0040155E | 7C 5E                    | jl pythagoras.4015BE                    | ; Salta si es menor

Como veis, el resultado de la resta da 7A (122) que al ser mayor que 4 nos echa vilmente. Aquí de nuevo utiliza registros de 8 bits por lo que debemos tener cuidado con las operaciones matemáticas para no cometer errores, veamos un ejemplo para clarificar de aquí en adelante.

Utilizando 8 bits
-----------------
12 - 98 = 7A que en decimal es 122

Utilizando 16 bits
------------------
0012 - 0098 = FF7A que en decimal es -134

Ahora ya veis la diferencia entre FC (252) y FFFC (-4). Estrictamente, el crackme comprueba el rango entre 4 (4) y FC (122) al trabajar con registros de 8 bits pero nosotros, como veremos más adelante tomaremos el rango entre 4 y -4. De momento, para poder continuar depurando cambiamos los dos primeros caracteres del serial de 12 a 98, ya que 98 – 98 = 0 y cumple la condición anterior.

Introducimos Nombre: deurus y Serial: 9834567890

Segunda condición

Analicemos el siguiente código.

00401560 | F7 E0                    | mul eax                                 | ; EAX = EAX * EAX
00401562 | 8B D8                    | mov ebx,eax                             | ; EBX = EAX
00401564 | 0F B7 05 F4 31 40 00     | movzx eax,word ptr ds:[4031F4]          | ; EAX = 3456 (4 dígitos siguientes del serial)
0040156B | F7 E0                    | mul eax                                 | ; EAX = EAX * EAX
0040156D | 03 D8                    | add ebx,eax                             | ; EBX = EBX + EAX
0040156F | 0F B7 05 F6 31 40 00     | movzx eax,word ptr ds:[4031F6]          | ; EAX = 7890 (4 últimos dígitos del serial)
00401576 | F7 E0                    | mul eax                                 | ; EAX = EAX * EAX
00401578 | 33 C3                    | xor eax,ebx                             | ; EAX
0040157A | 75 42                    | jne pythagoras.4015BE                   | ; Salta si el flag ZF no se activa

En resumen:

  • 98 * 98 = 5A40 (98²)
  • 3456 * 3456 = 0AB30CE4 (3456²)
  • 0AB36724 + 5A40 = 0AB36724
  • 7890 * 7890 = 38C75100 (7890²)
  • 38C75100 XOR 0AB36724 = 32743624
  • Si el resultado del XOR no es cero nuestro serial no pasa la comprobación.

Es decir, Pitágoras entra en escena -> 7890² = 98² + 3456²

Serial = aabbbbcccc

Tercera condición

Finalmente comprueba lo siguiente:

0040157C | 66 A1 F6 31 40 00        | mov ax,word ptr ds:[4031F6]             | ; AX = 7890
00401582 | 66 2B 05 F4 31 40 00     | sub ax,word ptr ds:[4031F4]             | ; AX = 7890 - 3456 = 443A
00401589 | 2C 08                    | sub al,8                                | ; AL = 3A - 8 = 32
0040158B | 75 31                    | jne pythagoras.4015BE                   | ; Si el resultado de la resta no ha sido cero, serial no válido
0040158D | 6A 30                    | push 30                                 |
0040158F | 68 B0 31 40 00           | push pythagoras.4031B0                  | ;004031B0:":-) Well done!!!"
00401594 | 68 7F 31 40 00           | push pythagoras.40317F                  | ;0040317F:"Bravo, hai trovato il seriale di questo CrackMe!"
00401599 | FF 75 08                 | push dword ptr ds:[ebp+8]               |

En resumen:

  • 7890 – 3456 – 8 = 0

Creación del Keygen

Nuestro serial tiene que cumplir tres condiciones para ser válido.

  • a – SUMNOMBRE debe estar entre 4 y -4
  • c² = a² + b²
  • c – b – 8 = 0

Como hemos dicho anteriormente, tomaremos el SUMNOMBRE y le sumaremos y restaremos valores siempre y cuando el resultado esté entre 4 y -4. Para deurus hemos dicho que el SUMNOMBRE es 98 por lo que los posibles valores de «a» se pueden ver debajo. Además debemos tener en cuenta que el crackme solo lee los 9 primeros dígitos del nombre.

98-4 = 94		
98-3 = 95		
98-2 = 96		
98-1 = 97		
98-0 = 98		
98+1 = 99		
98+2 = 9A		
98+3 = 9B		
98+4 = 9C

Es evidente que para encontrar el valor de «c» vamos a tener que utilizar fuerza bruta chequeando todos los valores  de «b» comprendidos entre 0 y FFFF (65535). Además, como trabajaremos en un lenguaje de alto nivel, debemos descartar los resultados decimales. Esto nos limitará los seriales válidos asociados a un determinado nombre. Si realizáramos el keygen en ensamblador obtendríamos bastantes más seriales válidos.

Una vez encontrados los valores enteros de la operación «c² = a² + b²», se debe cumplir que «c – b – 8 = 0», lo que nos limitará bastante los resultados.

    Private Sub btn_generar_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles btn_generar.Click
        Try
            If txt_nombre.TextLength > 5 Then
                lst_serials.Items.Clear()
                Dim tmp, c, cx As String
                Dim sumanombre, tmp2 As Integer
                If txt_nombre.TextLength > 9 Then tmp2 = 8 Else tmp2 = txt_nombre.TextLength - 1
                'Calculo el SUMNOMBRE
                For i = 0 To tmp2
                    sumanombre += Asc(Mid(txt_nombre.Text, i + 1, 1)) 'Acumulo suma
                    tmp = Strings.Right(Hex(sumanombre).ToString, 2)  'Solo 8 bits (Registro AL)
                    sumanombre = Val("&H" & tmp) 'Paso a decimal
                Next
                tmp = Strings.Right(Hex(sumanombre).ToString, 2)
                sumanombre = CInt("&H" & tmp)
                txtdebug.Text = "- SumNombre = " & Hex(sumanombre) & vbCrLf
                txtdebug.Text &= "----------------------------------------------" & vbCrLf
                Dim a(8) As Integer
                '
                'a - sumanombre >=4 y <=4
                '
                a(0) = sumanombre - 4
                a(1) = sumanombre - 3
                a(2) = sumanombre - 2
                a(3) = sumanombre - 1
                a(4) = sumanombre
                a(5) = sumanombre + 1
                a(6) = sumanombre + 2
                a(7) = sumanombre + 3
                a(8) = sumanombre + 4
                txtdebug.Text &= "- Posibles valores de 'a'" & vbCrLf
                For i = 0 To a.Length - 1
                    txtdebug.Text &= Hex(a(i)) & " "
                Next
                txtdebug.Text &= "----------------------------------------------" & vbCrLf
                txtdebug.Text &= "- Buscando valores de b y c" & vbCrLf
                txtdebug.Text &= "Serial = aabbbbcccc" & vbCrLf
                '
                'c = sqr(a^2 + b^2)
                '
                txtdebug.Text &= "(1) c = raiz(a^2 + b^2)" & vbCrLf
                txtdebug.Text &= "(2) c - b - 8 = 0" & vbCrLf
                For i = 0 To a.Length - 1 ' todas las posibilidades de a
                    For b = 0 To 65535 'b -> 0000 - FFFF
                        c = Math.Sqrt(a(i) ^ 2 + b ^ 2)
                        If c.Contains(".") Then 'busco enteros
                        Else
                            cx = c - b - 8
                            cx = Hex(cx).PadLeft(4, "0"c)
                            lbl_info.Text = cx
                            If cx = "0000" Then
                                txtdebug.Text &= " (1) " & Hex(c).PadLeft(4, "0"c) & " = raiz(" & Hex(a(i)).PadLeft(2, "0"c) & "^2 + " & Hex(b).PadLeft(4, "0"c) & "^2)" & vbCrLf
                                lst_serials.Items.Add(Hex(a(i)).PadLeft(2, "0"c) & Hex(b).PadLeft(4, "0"c) & Hex(c).PadLeft(4, "0"c))
                                txtdebug.Text &= " (2) " & Hex(c).PadLeft(4, "0"c) & " - " & Hex(b).PadLeft(4, "0"c) & " - 8 = 0" & vbCrLf
                            End If
                        End If
                        Application.DoEvents()
                    Next
                Next
                lbl_info.Text = "Búsqueda finalizada"
            End If
        Catch ex As Exception
            MsgBox(ex.ToString)
        End Try

Enlaces

ChatGPT vs CTF matemático

por ·Sin comentarios

El reto

Se nos proporciona la imagen anterior y se nos invita a resolver la ecuación para el menor entero positivo que representa cada fruta. La solución del reto es concatenar «Flag-» a la suma de los valores de las tres frutas.

Análisis inicial

El enunciado es breve pero ya nos adelanta que existen varias soluciones y que además sólo quieren los números más pequeños que podamos encontrar.

Las frutas están muy bien y son muy sanas pero a nosotros se nos hace más sencillo plantear la ecuación con letras.

\begin{align}
&  \frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=4\\
\end{align}

Para arrojar algo de luz veamos la representación gráfica en 2D y 3D con la ayuda de Desmos.

2D
3D

Las gráficas más que luz nos traen oscuridad de modo que preguntemos a ChatGPT.

ChatGPT

resuelve: (x/y+z)+(y/x+z)+(z/x+y)=4 para enteros positivos

Dado que las variables x, y, z son enteros positivos, podemos intentar encontrar una solución para la ecuación bajo estas condiciones. Sin embargo, encontrar una solución exacta puede ser complejo debido a la naturaleza no lineal de la ecuación. Aun así, podemos intentar algunos enfoques:

  • Prueba y error: Podemos probar diferentes combinaciones de valores enteros positivos para x, y, z y ver si satisfacen la ecuación.
  • Análisis de casos específicos: Podemos comenzar analizando casos más simples, como cuando dos de las variables son iguales, y luego ampliar nuestra búsqueda desde allí.
  • Análisis gráfico o numérico: Utilizando herramientas gráficas o numéricas, podríamos identificar posibles soluciones y luego verificar si son enteros positivos.

Voy a realizar un análisis numérico con un rango limitado de valores para ver si encontramos alguna solución que cumpla con las condiciones. Vamos a probar con valores de 1 a 10 para cada variable.

El análisis numérico para valores de en el rango de 1 a 10 no ha encontrado ninguna solución que satisfaga la ecuación. Esto sugiere que, dentro de este rango, no existen combinaciones de enteros positivos que cumplan con la ecuación.

Dado que la ecuación es bastante compleja y no lineal, es posible que las soluciones, si existen, se encuentren fuera del rango considerado o que requieran un enfoque diferente para ser identificadas. Si tienes un rango específico de valores en mente o si hay alguna otra restricción o contexto relevante, por favor házmelo saber para poder ajustar el análisis en consecuencia.

Básicamente nos está invitando a utilizar prueba y error para encontrar una solución, y el prueba y error de las matemáticas no es más que la fuerza bruta en programación.

El código

Partiendo del problema anterior dame un código en python que realice una comprobación recursiva de todas las variables con un rango de 1 a 999.

soluciones = []
rango_valores_x = range(1, 999)
rango_valores_y = range(1, 999)
rango_valores_z = range(1, 999)

for x in rango_valores_x:
    for y in rango_valores_y:
        for z in rango_valores_z:
            # Calculamos el valor de la expresión para cada combinación de x, y, z
            valor = x / (y + z) + y / (x + z) + z / (x + y)
            # Comprobamos si el valor es igual a 4 y agregamos la solución a la lista
            if abs(valor - 4) < 1e-6:  # Usamos una pequeña tolerancia para evitar errores de precisión
                soluciones.append((x, y, z))

print(soluciones)

Dejo resaltada la línea 12 del código ya que en ella reside el problema. Está comprobando con un margen de tolerancia de 10-6 ya que el resultado de las diferentes fracciones no da como resultado exacto 4. Esto es un problema ya que nosotros necesitamos que de exactamente 4 para validar los valores enteros de x, y y z. Pongo un ejemplo para el que se haya perdido con una solución válida para la tolerancia 10-6 siendo x=2, y=264 y z=993.

\begin{align}
&  \frac{2}{264+993}+\frac{264}{2+993}+\frac{993}{2+264}=4.000000429\\
\end{align}

En otras palabras, ChatGPT nos ha brindado una solución aproximada que no sirve para nuestro propósito. Seguimos probando con el código anterior quitando la tolerancia y con rangos mayores hasta que en 106 paro. Me acaba de quedar claro que con la fuerza bruta no vamos a ninguna parte, o más bien, no tenemos capacidad de computación para resolverlo de ésta manera.

¿Qué está pasando?

Lo que pasa es que estamos ante una ecuación algebraica de 3 incógnitas que deben ser enteros positivos cuya solución se alcanza mediante la teoría de curvas elípticas.

Curvas elípticas

Las curvas elípticas son fundamentales en matemáticas avanzadas, representadas por la ecuación y2=x3+Ax+B, donde A y B son constantes. Estas curvas son un punto de encuentro entre la geometría, la teoría de números y el álgebra, ofreciendo un campo rico para la exploración y el análisis. En este CTF, nos enfocaremos en los puntos racionales de las curvas elípticas. Utilizando el método tangente-secante, un procedimiento geométrico iterativo, buscaremos ampliar un conjunto finito de soluciones conocidas a la ecuación de la curva. Este método nos permite indagar en la estructura de las soluciones racionales, que potencialmente pueden ser infinitas. Además, estableceremos una conexión entre las soluciones enteras de las ecuaciones diofánticas y los puntos racionales en las curvas elípticas partiendo de la ecuación (1) especificada en el análisis inicial. A pesar de su aparente simplicidad, esta ecuación es conocida por presentar soluciones mínimas de gran tamaño.

Adecuación

Antes de nada, necesitamos saber el grado de la ecuación, de modo que planteamos la ecuación en forma polinómica estándar deshaciéndonos de los denominadores.

\begin{align}
\begin{split}
n(a+b)(b+c)(c+a)=a(a+b)(c+a)+b(b+c)(a+b)+c(c+a)(b+c)
\end{split}
\end{align}

Ahora necesitamos expandir y simplificar para llegar a la conclusión de que estamos ante una ecuación diofántica de grado 3. Este proceso es engorroso por la cantidad de términos a manejar así que vamos a utilizar Mathematica como software de respaldo para finalmente obtener el polinomio en la forma de Weierstrass según la ecuación 4.

\begin{align}
&  y^2=x^3+109x^2+224x\\
\end{align}

donde:

\begin{align}
x = \frac{−28(a+b+2c)}{(6a+6b−c)}\\
y = \frac{364(a−b)}{(6a+6b−c)}
\end{align}

Las relación entre la ecuación 3 y los puntos de la curva elíptica se establecen mediante la ecuación 4. Las transformaciones entre las soluciones (a, b, c) y los puntos (x, y) en la curva elíptica vienen dados por las ecuaciones 5 y 6. Con estas transformaciones, cada solución de la ecuación diofántica se puede representar como un punto en la curva elíptica, y las operaciones de suma de puntos en la curva elíptica pueden usarse para encontrar nuevas soluciones de la ecuación diofántica.

Mathematica

El código que tenéis a continuación pertenece al gran trabajo de Aditi Kulkarni [7], que además nos da el resultado para cualquier valor de n. Ojo porque para n=4 el resultado tiene 81 dígitos, para n=6 tiene 134, para n=10 tiene 190 y para n=12 asciende a 2707 dígitos. 

(* Asignar un valor numérico a n *)
n = 4;
(* Definir la ecuación de una curva elíptica en términos de n *)
curve4 = y^2 == x^3 + (4*n^2 + 12*n - 3)*x^2 + 32*(n + 3)*x;
(* Encontrar un punto racional en la curva que no sea (4,0) *)
P4 = {x, y} /. First[FindInstance[curve4 && x != 4 && y != 0, {x, y}, Integers]];
(* Función para calcular la pendiente entre dos puntos en la curva, 
   o la derivada en el punto si son iguales *)
Slope4[{x1_, y1_}, {x2_, y2_}] := 
  If[x1 == x2 && y1 == y2, 
     ImplicitD[curve4, y, x] /. {x -> x1, y -> y1}, 
     (y2 - y1)/(x2 - x1)];
(* Función para calcular la intersección en y de la línea entre dos puntos 
   o la tangente en el punto si son iguales *)
Intercept4[{x1_, y1_}, {x2_, y2_}] := y1 - Slope4[{x1, y1}, {x2, y2}]*x1; 
(* Función para encontrar el siguiente punto racional en la curva *)
nextRational4[{x1_, y1_}, {x2_, y2_}] := 
  {Slope4[{x1, y1}, {x2, y2}]^2 - CoefficientList[curve4[[2]], x][[3]] - x1 - x2, 
   -Slope4[{x1, y1}, {x2, y2}]^3 + Slope4[{x1, y1}, {x2, y2}]*(CoefficientList[curve4[[2]], x][[3]] + x1 + x2) - Intercept4[{x1, y1}, {x2, y2}]};
(* Función para convertir un punto en la curva elíptica a una solución diofántica *)
ellipticToDiophantine[n_, {x_, y_}] := 
  {(8*(n + 3) - x + y)/(2*(4 - x)*(n + 3)), 
   (8*(n + 3) - x - y)/(2*(4 - x)*(n + 3)), 
   (-4*(n + 3) - (n + 2)*x)/((4 - x)*(n + 3))};
(* Usar nextRational4 para iterar desde P4 hasta encontrar una solución 
   válida y positiva para la ecuación diofántica *)
sol4 = ellipticToDiophantine[n, 
   NestWhile[nextRational4[#, P4] &, P4, 
     ! AllTrue[ellipticToDiophantine[n, #], Function[item, item > 0]] &]];
(* Escalar la solución para obtener enteros mínimos *)
MinSol4 = sol4*(LCM @@ Denominator[sol4])
(* Suma de las tres variables*)
Total[MinSol4]

Solución

Concatenando Flag- con el resultado de Mathematica tenemos la ansiada flag.

Flag-195725546580804863527010379187516702463973843196699016314931210363268850137105614

Conclusiones

ChatGPT ha demostrado ser eficaz en el análisis y la resolución de problemas, siempre que se le proporcione el contexto adecuado. Sin embargo, es importante ser conscientes de que la respuesta proporcionada puede ser aproximada, especialmente si la solución requiere una gran cantidad de recursos computacionales. Por ejemplo, al trabajar con una ecuación diofántica y valores específicos para (x) e (y), ChatGPT puede ayudar a calcular puntos como (P), (2P), (3P), etc., pero hay que tener en cuenta que los resultados para estos puntos pueden ser estimaciones.

Finalmente, os invito a leer la solución de Mingliang Z. [4], en la que se resuelve el problema por completo y de forma muy detallada.

Enlaces