por ·1 comentario

Introducción

Hoy tenemos aquí un crackme de los que te hacen temblar las conexiones neuronales. Estamos acostumbrados al típico serial asociado a un nombre y a veces nos sorprenden.

El crackme data del año 2000, está realizado por aLoNg3x y lo tenéis colgado en crackmes.de. En crackmes.de también disponéis de una solución muy elegante realizada por cronos, pero que no acaba de saciar nuestro afán de descubrir todas las soluciones posibles.

El algoritmo

Abrimos el crackme con Olly y enseguida encontramos la rutina de comprobación junto con los mensajes de éxito y error. Os dejo la rutina comentada como siempre.

004012D7   |.  83C4 08             ADD ESP,8                                 ;  
004012DA   |.  09C0                OR EAX,EAX                                ;  
004012DC   |. /74 16               JE SHORT Zebrone.004012F4                 ;  Salta a Bad boy
004012DE   |. |6A 00               PUSH 0                                    ; /Style = MB_OK|MB_APPLMODAL
004012E0   |. |68 26324000         PUSH Zebrone.00403226                     ; |Title = "Great !!!"
004012E5   |. |68 30324000         PUSH Zebrone.00403230                     ; |Text = "Congratulations, you have cracked the Zebra Crackme ver 1.1"
004012EA   |. |FF75 08             PUSH [ARG.1]                              ; |hOwner = 0011067C ('Zebra - aLoNg3x - 1.1 Version',class='#32770')
004012ED   |. |E8 C6010000         CALL <JMP.&USER32.MessageBoxA>            ; \MessageBoxA
004012F2   |. |EB 14               JMP SHORT Zebrone.00401308
004012F4   |> \6A 00               PUSH 0                                    ; /Style = MB_OK|MB_APPLMODAL
004012F6   |.  68 F8314000         PUSH Zebrone.004031F8                     ; |Title = "Hmmmm :P"
004012FB   |.  68 01324000         PUSH Zebrone.00403201                     ; |Text = "Sorry... The Serial isn't correct :Þ"
00401300   |.  FF75 08             PUSH [ARG.1]                              ; |hOwner = 0011067C ('Zebra - aLoNg3x - 1.1 Version',class='#32770')
00401303   |.  E8 B0010000         CALL <JMP.&USER32.MessageBoxA>            ; \MessageBoxA
00401308   |>  31C0                XOR EAX,EAX
0040130A   |.  40                  INC EAX
0040130B   |.  EB 39               JMP SHORT Zebrone.00401346
0040130D   |>  6A 00               PUSH 0                                    ; /Result = 0
0040130F   |.  FF75 08             PUSH [ARG.1]                              ; |hWnd = 0011067C ('Zebra - aLoNg3x - 1.1 Version',class='#32770')
00401312   |.  E8 89010000         CALL <JMP.&USER32.EndDialog>              ; \EndDialog
00401317   |.  31C0                XOR EAX,EAX
00401319   |.  40                  INC EAX
0040131A   |.  EB 2A               JMP SHORT Zebrone.00401346
0040131C   |>  6A 00               PUSH 0                                    ; /Style = MB_OK|MB_APPLMODAL
0040131E   |.  68 40304000         PUSH Zebrone.00403040                     ; |Title = "Zebra ver. 1.1"
00401323   |.  68 4F304000         PUSH Zebrone.0040304F                     ; |Text = "This is the 1.1 Zebra Crackme, Thanks to Quequero and Koma, to have said me a bug of the previous version. (It was due to an orrible cpu appoximation). As usually you cannot patch this .EXE, you've to find one of the many correct solut"...
00401328   |.  FF75 08             PUSH [ARG.1]                              ; |hOwner = 0011067C ('Zebra - aLoNg3x - 1.1 Version',class='#32770')
0040132B   |.  E8 88010000         CALL <JMP.&USER32.MessageBoxA>            ; \MessageBoxA
00401330   |.  31C0                XOR EAX,EAX
00401332   |.  40                  INC EAX
00401333   |.  EB 11               JMP SHORT Zebrone.00401346
00401335   |>  6A 00               PUSH 0                                    ; /Result = 0
00401337   |.  FF75 08             PUSH [ARG.1]                              ; |hWnd = 0011067C ('Zebra - aLoNg3x - 1.1 Version',class='#32770')
0040133A   |.  E8 61010000         CALL <JMP.&USER32.EndDialog>              ; \EndDialog
0040133F   |.  31C0                XOR EAX,EAX
00401341   |.  40                  INC EAX
00401342   |.  EB 02               JMP SHORT Zebrone.00401346
00401344   |>  31C0                XOR EAX,EAX
00401346   |>  C9                  LEAVE
00401347   \.  C2 1000             RETN 10
================================================================
0040134A   /$  55                  PUSH EBP
0040134B   |.  89E5                MOV EBP,ESP
0040134D   |.  83EC 68             SUB ESP,68
00401350   |.  FF75 08             PUSH [ARG.1]                              ; /x1
00401353   |.  E8 78010000         CALL <JMP.&CRTDLL.atof>                   ; \atof
00401358   |.  DD55 E8             FST QWORD PTR SS:[EBP-18]
0040135B   |.  83EC 08             SUB ESP,8
0040135E   |.  DD1C24              FSTP QWORD PTR SS:[ESP]
00401361   |.  E8 82010000         CALL <JMP.&CRTDLL.floor>
00401366   |.  DD5D F8             FSTP QWORD PTR SS:[EBP-8]
00401369   |.  FF75 0C             PUSH [ARG.2]                              ; /x2
0040136C   |.  E8 5F010000         CALL <JMP.&CRTDLL.atof>                   ; \atof
00401371   |.  DD55 D8             FST QWORD PTR SS:[EBP-28]
00401374   |.  83EC 08             SUB ESP,8
00401377   |.  DD1C24              FSTP QWORD PTR SS:[ESP]
0040137A   |.  E8 69010000         CALL <JMP.&CRTDLL.floor>
0040137F   |.  83C4 18             ADD ESP,18
00401382   |.  DD55 F0             FST QWORD PTR SS:[EBP-10]
00401385   |.  DC4D F8             FMUL QWORD PTR SS:[EBP-8]
00401388   |.  D9EE                FLDZ
0040138A   |.  DED9                FCOMPP                                    ;  floor(x1)*floor(x2)=0 ???
0040138C   |.  DFE0                FSTSW AX                                  ;  <<Store status word
0040138E   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
0040138F   |.  75 07               JNZ SHORT Zebrone.00401398                ;  Si salta todo OK
00401391   |.  31C0                XOR EAX,EAX
00401393   |.  E9 96000000         JMP Zebrone.0040142E                      ;  Bad boy
00401398   |>  DD45 F8             FLD QWORD PTR SS:[EBP-8]                  ;  <<Floating point load
0040139B   |.  DC5D F0             FCOMP QWORD PTR SS:[EBP-10]               ;  x1 = x2 ???
0040139E   |.  DFE0                FSTSW AX                                  ;  <<Store status word
004013A0   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
004013A1   |.  75 07               JNZ SHORT Zebrone.004013AA                ;  Si salta todo OK
004013A3   |.  31C0                XOR EAX,EAX
004013A5   |.  E9 84000000         JMP Zebrone.0040142E                      ;  Bad boy
004013AA   |>  DD45 F8             FLD QWORD PTR SS:[EBP-8]                  ;  <<Floating point load
004013AD   |.  DD5D C8             FSTP QWORD PTR SS:[EBP-38]
004013B0   |.  D9E8                FLD1                                      ;  Carga 1 en el stack
004013B2   |.  DD55 C0             FST QWORD PTR SS:[EBP-40]                 ;  <<Floating point store
004013B5   |.  DC5D C8             FCOMP QWORD PTR SS:[EBP-38]               ;  x1 > 1 ???
004013B8   |.  DFE0                FSTSW AX                                  ;  <<Store status word
004013BA   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
004013BB   |.  77 2D               JA SHORT Zebrone.004013EA                 ;  Si salta bad boy
004013BD   |.  DF2D 38304000       FILD QWORD PTR DS:[403038]                ;  <<Load integer>> 2540BE400 = 10^10
004013C3   |.  DD55 B8             FST QWORD PTR SS:[EBP-48]                 ;  <<Floating point store
004013C6   |.  DC5D C8             FCOMP QWORD PTR SS:[EBP-38]               ;  x1 < 10^10 ???
004013C9   |.  DFE0                FSTSW AX                                  ;  <<Store status word
004013CB   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
004013CC   |.  72 1C               JB SHORT Zebrone.004013EA                 ;  Si salta bad boy
004013CE   |.  DD45 F0             FLD QWORD PTR SS:[EBP-10]                 ;  <<Floating point load
004013D1   |.  DD5D B0             FSTP QWORD PTR SS:[EBP-50]                ;  <<Store and pop
004013D4   |.  DD45 C0             FLD QWORD PTR SS:[EBP-40]                 ;  <<Floating point load
004013D7   |.  DC5D B0             FCOMP QWORD PTR SS:[EBP-50]               ;  x2 > 1 ???
004013DA   |.  DFE0                FSTSW AX                                  ;  <<Store status word
004013DC   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
004013DD   |.  77 0B               JA SHORT Zebrone.004013EA                 ;  Si salta bad boy
004013DF   |.  DD45 B8             FLD QWORD PTR SS:[EBP-48]                 ;  <<Floating point load>> carga 10^10
004013E2   |.  DC5D B0             FCOMP QWORD PTR SS:[EBP-50]               ;  x2 < 10^10 ???
004013E5   |.  DFE0                FSTSW AX                                  ;  <<Store status word
004013E7   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
004013E8   |.  73 04               JNB SHORT Zebrone.004013EE                ;  Salta si menor
004013EA   |>  31C0                XOR EAX,EAX
004013EC   |.  EB 40               JMP SHORT Zebrone.0040142E                ;  Bad boy
004013EE   |>  DD45 F8             FLD QWORD PTR SS:[EBP-8]                  ;  <<Floating point load>> carga x1
004013F1   |.  D9FE                FSIN                                      ;  Sin(x1)
004013F3   |.  DD5D A8             FSTP QWORD PTR SS:[EBP-58]                ;  <<Store and pop
004013F6   |.  DD45 F0             FLD QWORD PTR SS:[EBP-10]                 ;  <<Floating point load>> carga x2
004013F9   |.  D9FE                FSIN                                      ;  Sin(x2)
004013FB   |.  DD5D A0             FSTP QWORD PTR SS:[EBP-60]                ;  <<Store and pop
004013FE   |.  DD45 A8             FLD QWORD PTR SS:[EBP-58]                 ;  <<Floating point load
00401401   |.  DC4D A0             FMUL QWORD PTR SS:[EBP-60]                ;  Sin(x1) * Sin(x2)
00401404   |.  DF2D 30304000       FILD QWORD PTR DS:[403030]                ;  <<Load integer>> 2386F26FC10000 = 10^16
0040140A   |.  DEC9                FMULP ST(1),ST                            ;  10^16 * (Sin(x1) * Sin(x2))
0040140C   |.  83EC 08             SUB ESP,8
0040140F   |.  DD1C24              FSTP QWORD PTR SS:[ESP]                   ;  <<Store and pop
00401412   |.  E8 D1000000         CALL <JMP.&CRTDLL.floor>
00401417   |.  83C4 08             ADD ESP,8
0040141A   |.  DD5D 98             FSTP QWORD PTR SS:[EBP-68]
0040141D   |.  D9EE                FLDZ                                      ;  <<Load 0.0 onto stack
0040141F   |.  DC5D 98             FCOMP QWORD PTR SS:[EBP-68]               ;  10^16 * (Sin(x1) * Sin(x2)) = 0 ???
00401422   |.  DFE0                FSTSW AX
00401424   |.  9E                  SAHF                                      ;  <<Store AH into FLAGS
00401425   |.  75 05               JNZ SHORT Zebrone.0040142C                ;  Si NO salta todo OK
00401427   |.  31C0                XOR EAX,EAX
00401429   |.  40                  INC EAX
0040142A   |.  EB 02               JMP SHORT Zebrone.0040142E
0040142C   |>  31C0                XOR EAX,EAX
0040142E   |>  C9                  LEAVE
0040142F   \.  C3                  RETN

La primera dificultad que podemos encontrar es que utiliza instrucciones FPU y coma flotante, ya que si no tenemos la vista entrenada nos puede resultar un engorro. Superado esto, la rutina de comprobación se puede resumir así:

  • x1 * x2 != 0
  • x1 != x2
  • x1 > 1 y < 10^10
  • x2 > 1 y < 10^10
  • Floor[10^16 * sin(x1) * sin(x2)] = 0

A priori no parece que tenga mucha dificultad, pero vamos a analizarlo más concienzudamente. Necesitamos que la parte entera del resultado de la multiplicación sea 0, algo que parece sencillo, pero fíjate que la constante 10^16 nos obliga a su vez, a que el resultado del seno sea muy pequeño, cosa que como comprobaréis limita mucho los resultados satisfactorios.

Repasando trigonometría

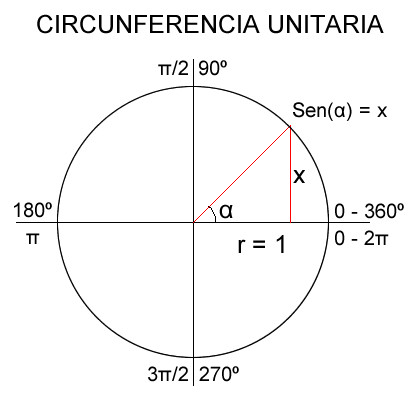
Cuando nos enseñó nuestro profesor la función del seno nos hizo el siguiente dibujo:

circunferencia_e

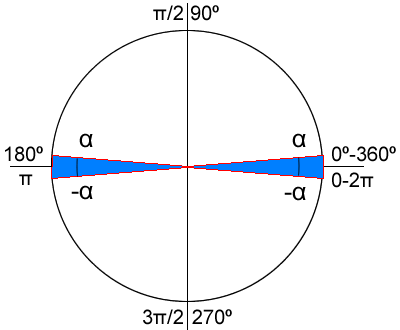
Partiendo de la circunferencia unitaria, podemos concluir que el seno de alpha es igual a la altura x. Como lo que nos interesa a nosotros es que el seno sea muy pequeño, en realidad estamos buscando que la x sea lo más pequeña posible. Llegamos entonces a la conclusión de que las soluciones para enteros entre 1 y 10^10 van a ser muy reducidas. Además nos percatamos que el ángulo alpha va a tener que estar muy proximo a 0º – 360 (0 – 2π) y a 180º (π). En el siguiente gráfico queda claro el estrecho margen en el que nos movemos.

circunferencia_angulos_e

Si habéis leído la solución de cronos ahora le encontraréis algo más de sentido a por que él utilizó fracciones continuas de π y cogió como resultado los numeradores más cercanos a 10^10, en su caso 245850922 y 411557987.

Análisis operacional

Vamos a analizar un ejemplo operacional.

sin( x rad)
sin(245850922) = 6,1180653830011163142712109862972e-9
sin(411557987) = 2,536716051963676479648989773448e-9

sin(245850922)*sin(411557987) = 1,5519794664022230015882605365808e-17

10^16 * 1,5519794664022230015882605365808e-17 = 0,15519794664022230015882605365808

Floor(0,15519794664022230015882605365808) = 0

Como veis, el exponente negativo (^-17) debe ser mayor que el positivo (^16) para tener éxito.

Fuerza bruta

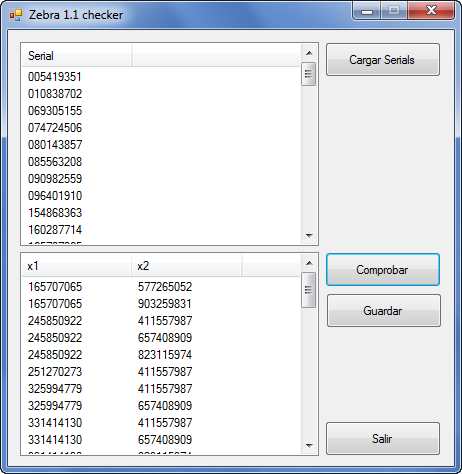
Lo que vamos a hacer a continuación es buscar todos los senos con exponente negativo ^-8 ó ^-9 de enteros entre 1 y 10^10, y vamos a cruzar los resultados para determinar todos los resultados válidos.

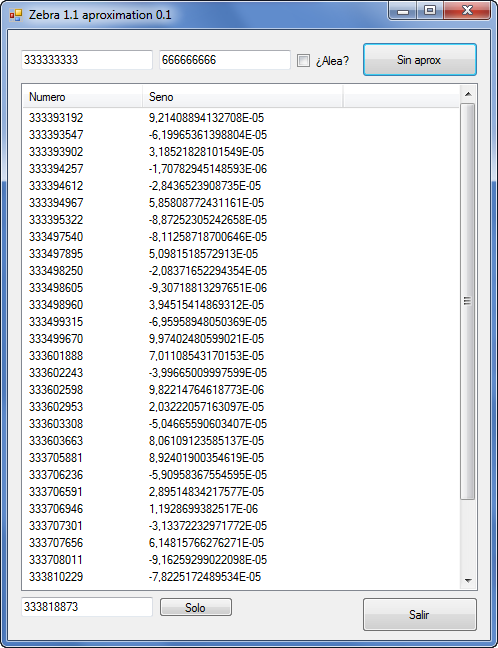
Preparamos el programa y le dejamos trabajar. En principio vamos a filtrar todos los resultados que tengan exponente negativo y luego ya aislaremos los que nos interesan. Esto lo hago por curiosidad.

aprox

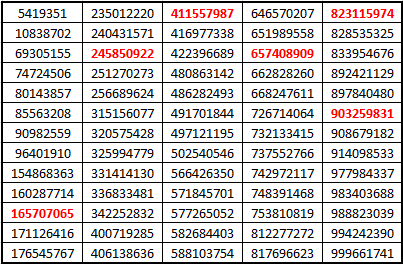
La fuerza bruta nos arroja 63663 resultados con exponente negativo entre ^-5 y ^-9, de los cuales solamente nos quedamos con 65, que son los comprendidos a exponentes de entre ^-8 y ^-9. Los números mágicos son los siguientes:

magicnumbers

Los rojos son exponentes ^-9, el resto ^-8.

La mayoría de estos números solo valen con ciertas combinaciones, de hecho, ninguno vale para todos. Esto se debe, a parte del propio exponente, a que hay senos positivos y negativos y para hacer válido a un seno negativo hay que combinarlo con otro negativo. Esto último se debe únicamente a la interpretación que hace el crackme.

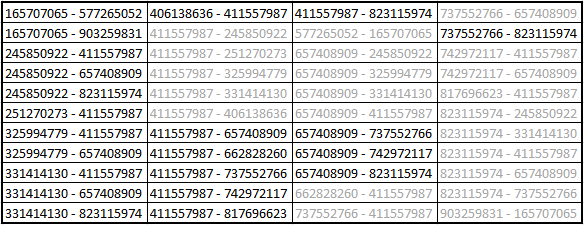
 Finalmente cruzamos los resultados y obtenemos 44 combinaciones de seriales válidos que si obviamos repeticiones se reducen a la mitad.

 checker

Combinaciones válidas:

seriales

Conclusiones

Podemos concluir que para cada 10^10 enteros hay 22 soluciones posibles. Finalmente comentar que si aLoNg3x no hubiera puesto el límite en 10^10, habría soluciones infinitas.

Links

Blooper Tech Movie XIV – Parque Jurásico
En Parque Jurásico (1993), la informática no es solo un elemento narrativo, es una pieza clave del suspense y del
Stego Ph0n3
Un error que habitualmente cometo cuando me enfrento a todo tipo de retos (especialmente en CTFs) es empezar a procesar
VideoTutorial - KeyGen para el Crackme#1 de WinFan
http://youtu.be/b9-GdmIQINQ Lista de reproducción
Reto Stego 1 de Hacker Games
Cambio de extensión Imagen oculta Descifrando el mensaje Enlaces Cambio de extensión (paso opcional) Al descargar la imagen de la

por ·Sin comentarios

En Parque Jurásico (1993), la informática no es solo un elemento narrativo, es una pieza clave del suspense y del conflicto. A diferencia de otras películas donde las pantallas muestran interfaces ficticias o visualmente espectaculares pero irreales, Parque Jurásico opta por una aproximación sorprendentemente sobria y auténtica.

Durante bastantes escenas, se nos muestran terminales, ventanas de código y comandos que, lejos de ser decorativos, pertenecen a sistemas reales utilizados por programadores profesionales de principios de los años 90. Este detalle, que puede pasar desapercibido para el público general, resulta especialmente interesante desde un punto de vista técnico. En otras palabras, el trabajo de producción es excelente y destaca como una de las películas más respetuosas con la informática real de su época.

No es “código de película”: es software real

Uno de los puntos más interesantes es que el código que aparece en pantalla no fue escrito para la película. No hay pseudocódigo, ni pantallas diseñadas solo para quedar bonitas en cámara. Lo que se ve es software real, ejecutándose en el entorno Macintosh Programmer’s Workshop (MPW), el kit oficial de Apple para desarrolladores en aquellos años. El sistema operativo que se reconoce es un Macintosh clásico (System 7) corriendo sobre máquinas de la serie Quadra, auténticos pepinos para la época. Vamos, que cuando John Hammond decía aquello de «no hemos reparado en gastos», también iba en serio en lo informático.

«No hemos reparado en gastos»

En este punto no se le puede reprochar demasiado a la película. En líneas generales es bastante fiel a la novela, aunque la resolución del problema de seguridad se aborda de forma distinta. En el libro es el ingeniero Ray Arnold quien detecta el fallo y consigue reconducir la situación. En la película, sin embargo, el personaje desaparece cuando va a los barracones a restablecer la corriente del parque, con el resultado que todos conocemos.

Lo curioso es que muchos personajes sí cambian de forma notable con respecto al libro, el niño es mayor y más friki de los ordenadores, Ray Arnold no muere y acaba salvando la situación, o Gennaro es más atlético y bastante más valiente. Sin embargo, el gran disparate técnico permanece intacto.

En la novela se menciona de pasada a un equipo de informáticos de Cambridge que supuestamente colaboró en el diseño del software. Aun así, la puesta en marcha y la explotación del sistema recaen prácticamente en una sola persona, Dennis Nedry. Evidentemente, tanto al libro como al guion les viene de perlas que todo dependa de una única persona para que el desastre sea posible, pero cuesta aceptar que en un parque donde todo está duplicado, el control informático central dependa de una sola persona.

Curiosamente, en uno de los monitores de Nedry se puede ver una foto de Oppenheimer con la frase «Beginning of baby boom», de la que podemos sacar la conclusión de que Nedry es perfectamente consciente de que su trabajo puede tener consecuencias catastróficas e irreversibles. También es un maravilloso guiño del equipo de producción que nos está indicando exactamente donde se va originar el desastre.

Al final, Parque Jurásico no va de dinosaurios, ni siquiera de genética. Va de personas. Y, más concretamente, de personas con demasiado poder y muy pocos compañeros de equipo y poca supervisión.

Desde el punto de vista informático, la película es casi entrañable. Todo es serio, profesional y real… hasta que descubrimos que el sistema más complejo jamás construido depende, en la práctica, de un solo programador cabreado, mal pagado y con demasiadas líneas de código en la cabeza. Ningún comité de arquitectura, ninguna auditoría externa, ningún segundo par de ojos. Solo Dennis Nedry y su teclado. ¿Qué podía salir mal?

Lo curioso es que ni la película ni el libro se molestan en disimularlo demasiado. Te hablan de sistemas redundantes, de seguridad, de control absoluto… pero el corazón digital del parque es un castillo de naipes. Eso sí, un castillo de naipes programado en máquinas de primera, con software real y pantallas que hoy siguen pareciendo más creíbles que muchas producciones actuales.

Quizá por eso Parque Jurásico envejece tan bien. Porque, incluso cuando se equivoca, lo hace con honestidad. No intenta venderte magia disfrazada de tecnología. Te muestra ordenadores de verdad, código de verdad y errores muy humanos. Y al final, tanto en la novela como en la película, el mensaje es el mismo, puedes clonar dinosaurios, diseñar parques imposibles y rodearte de la mejor tecnología del mundo, que si todo depende de una sola persona, tarde o temprano, el sistema se vendrá abajo.

Y no, el problema no eran los dinosaurios, nunca lo fueron.

por ·Sin comentarios

Un error que habitualmente cometo cuando me enfrento a todo tipo de retos (especialmente en CTFs) es empezar a procesar el fichero proporcionado con todo tipo de herramientas como pollo sin cabeza. En el caso que nos ocupa se proporcionaba un fichero de audio WAV que procesé hasta con 4 herramientas diferentes antes de tomar aire y decidir simplemente escuchar el audio. Al escucharlo me di cuenta de que se trataba de una marcación por tonos comúnmente conocido como DTMF (Dual-Tone Multi-Frequency).

Decodificar DTMF

Con una rápida búsqueda por la web encontré una sencilla herramienta realizada en python llamada dtmf-decoder con la que enseguida obtenemos resultados. La herramienta es bastante sencilla, simplemente parte la señal en trozos, calcula la FFT (Fast Fourier Transform) para obtener las amplitudes y las compara con las de los tonos DTMF. Hay que tener en cuenta que el audio entregado es muy limpio y eso facilita mucho las cosas.

El siguiente comando nos devuelve los números marcados.

Como era de esperar, los números obtenidos no son la solución final aunque en este caso enseguida damos con que el tipo de codificación es simple y llanamente ASCII.

DTMF = 837283123119104521169510048951214811795119521101166363125
HEX  = 53 48 53 7B 77 68 34 74 5F 64 30 5F 79 30 75 5F 77 34 6E 74 3F 3F 7D
Solución: SHS{wh4t_d0_y0u_w4nt??}

por ·Sin comentarios

Cambio de extensión (paso opcional)

Al descargar la imagen de la web del reto vemos que tiene la extensión php y lo más probable es que no nos abra correctamente.

...
<br/>
<img src="steg1img.php"/>
<br/>
...

Abrimos la imagen con nuestro editor hexadecimal favorito y nos fijamos en la cabecera.

00000000h: 89 50 4E 47 0D 0A 1A 0A 00 00 00 0D 49 48 44 52 ; ‰PNG........IHDR

Renombramos entonces la extensión a png y continuamos.

Imagen oculta

Esta parte la afrontaremos con Steganabara, una herramienta muy útil que siempre uso cuando me enfrento a un reto «stego». En esta ocasión utilizaremos el análisis de color. Para ello pulsamos sobre «Analyse > Color table«.

02-12-2015 10-17-24

En la tabla de colores tenemos la descomposición de colores RGBA y su frecuencia de aparición. Ordenamos por frecuencia descendiente y hacemos doble clic sobre la fila para abrir la imagen resultante.

02-12-2015 10-21-16

A continuación un resumen de las imágenes obtenidas.

colortable

Como podéis observar, la imagen oculta es un código QR. Lo escaneamos con nuestra app preferida y obtenemos un texto encriptado.

dtsfwqutisvqtesymkuvabbujwhfecuvlshwopcyeghguywjvlaibflcacyahckyqvypjntfhihgtvyxeqakjwouldltuiuhbhjumgkxuugqahvwhotduqtahcknheypjetxpvlhxtlrpjagyjzcgijgfjmcupsslkzpuxegaillytlfbygeptzjtuzlvlwkzdznxqwpabbe

Descifrando el mensaje

A partir de aquí el reto pasa a ser de encriptación. Con el tiempo diferenciareis fácilmente el tipo de cifrado con sólo ver el texto. En este caso lo primero que se nos ocurre es comprobar dos cifrados clásicos como son el cifrado César y el Vigenere.

Tras desestimar el cifrado César realizamos un ataque de «fuerza bruta» al cifrado Vigenere mediante análisis estadístico. En la imagen que muestro a continuación se puede ver que la clave está cerca de ser «HPHQTC» pero todavía no se lee correctamente.

02-12-2015 10-56-29

Ya que la fuerza bruta de por sí no termina de darnos la respuesta correcta, pasamos a probar algo muy útil, esto es, descifrar por fuerza bruta pero dándole una palabra para comparar. En este caso en concreto vemos que una posible palabra que pudiera estar en el texto encriptado es «PASSWORD», probamos y reto terminado.

02-12-2015 10-57-14

Enlaces