Analizando…
Cargamos el crackme en Ollydbg y vamos a las «Referenced Strings«. Vemos una referencia muy interesante que se llama «checkkey«.
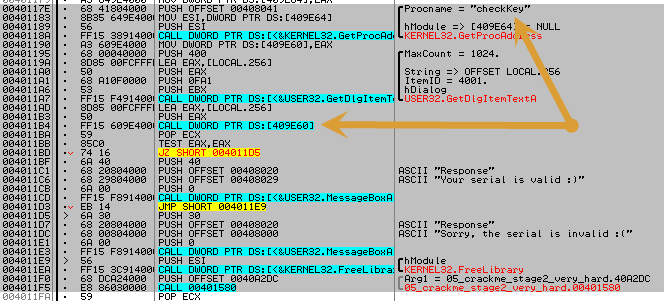
Pinchamos sobre ella y aparecemos aquí:
Vemos una referencia a «GetDlgItemTextA» y depués un Call también interesante, vamos a explorarlo.
Entendiendo la rutina de comprobación del serial
Dentro del Call hay dos bucles, uno realiza una operación con nuestro serial (bucle nombre) y el otro comprueba nuestro serial con «3d34273130276a» dígito a dígito (bucle comprobación).
Bucle nombre se puede resumir así:
MOVSX EAX,BYTE PTR DS:[EBX] --> Dígito a EAX XOR EAX,55 --> EAX xor 55 ... CMP BYTE PTR DS:[EBX],0 --> ¿hemos acabado? JNZ SHORT 10001022 --> bucle LEA ECX,DWORD PTR SS:[EBP-20] --> ECX = nuestro serial xoreado
Bucle comprobación se podría resumir así:
MOV EDX,10006000 --> EDX = "3d34273130276a" ... MOV AL,BYTE PTR DS:[ECX] --> AL = 1ºdígito serial xoreado CMP AL,BYTE PTR DS:[ECX+EDX] --> AL = 1ºdígito de EDX? JNZ SHORT 1000105A --> Si no son iguales bad boy INC ECX TEST AL,AL JNZ SHORT 1000104A --> bucle
Ejemplo para «deurus».
Nombre: d e u r u s
Ascii hex: 64 65 75 72 75 73
XOR 55: 31 30 20 27 20 26
Serial correcto XOReado: 3d 34 27 31 30 27 6a
XOR 55: 68 61 72 64 65 72 3F
Valor ascii: h a r d e r ?