Yoire PE Reversing Challenge (Crackme Very Hard)

26 agosto, 2014 por deurus·Sin comentarios

Aviso: Este crackme forma parte de una serie de pruebas de Yoire.com que todavía está en activo. Lo ético si continuas leyendo este manual es que no utilices la respuesta para completar la prueba sin esfuerzo. 😉

Saltando el Anti-Debug

Abrimos el crackme con Ollydbg y nos salta una protección Anti-Debug.

Si nos fijamos en las «Text Strings» vemos que es la clásica isDebuggerPresent. Pinchamos en ella y vemos claramente el salto que debemos forzar, se encuentra en el offset 401015. Podemos invertir el salto o cambiarlo a JMP para que salte siempre.

Rutina de comprobación del serial

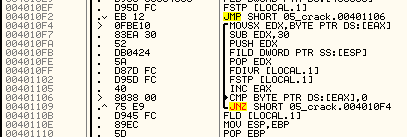
A simple vista vemos instrucciones como FILD y FIDIVR que trabajan con los registros FPU, por lo que tendremos que fijarnos en dichos registros.

Retomemos analizando la rutina de comprobación.

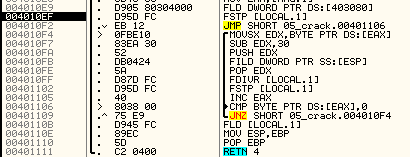
FLD DWORD PTR DS:[403080]    - Carga el entero "720300" en ST7
FSTP [LOCAL.1]               - Guarda "720300" en memoria (Local 1)
MOVSX EDX,BYTE PTR DS:[EAX]  - Coje nuestro primer dígito en ascii y lo carga en EDX
SUB EDX,30                   - Le resta 30 a EDX
PUSH EDX                     - Carga EDX en la pila
FILD DWORD PTR SS:[ESP]      - Carga el valor de EDX en ST0
POP EDX                      - Recupera el valor de la pila
FDIVR [LOCAL.1]              - Divide Local 1 entre nuestro dígito hex y lo guarda en ST0
FSTP [LOCAL.1]               - Guarda el resultado de ST0 en Local 1
INC EAX                      - Siguiente dígito
CMP BYTE PTR DS:[EAX],0      - Comprueba si quedan dígitos en nuestro serial
JNZ SHORT 05_crack.004010F4  - Bucle

Después de la rutina de comprobación simplemente comprueba el valor del resultado de la división con 1 y si es verdad serial válido.

Buscando un serial válido

Podríamos hacer fuerza bruta, pero en esta ocasión no es necesario ya que con la calculadora, boli y papel lo sacamos rápido.

720300 / 2 = 360150
360150 / 2 = 180075
180075 / 5 = 36015
36015  / 5 = 7203
7203   / 3 = 2401
2401   / 7 = 343
343    / 7 = 49
49     / 7 = 7
7      / 7 = 1

Por lo que un serial válido sería: 225537777

La rutina de comprobación del serial podría resumirse también así:

720300 MOD serial = 720300

Links

Tron - Reto IA de yoire.com

Introducción Objetivo del juego y normas Código inicial Primeras modificaciones Terminando la faena Código ganador Curiosidades Enlaces Introducción Hace tiempo

Los Pistoleros Solitarios

En una entrada anterior sobre cómo Expediente X abordó la tecnología de vanguardia, comenté que dedicaría un espacio a esos

Migas de pan

Se nos entrega el siguiente ELF: Extracción de la Flag Si nos fijamos en las líneas 41 a la 45

Mirror Crackmes.de

While Crackmes.de returns, I leave a couple of files for practice. Mientras vuelve Crackmes.de, os dejo un par de archivos para practicar.

1 2 3 … 30 Next »

ai challenge deurus ia inteligencia artificial programación reto Tr0n tron Yoire

Tron – Reto IA de yoire.com

29 agosto, 2015 por deurus·1 comentario

Introducción
Objetivo del juego y normas
Código inicial
Primeras modificaciones
Terminando la faena
Código ganador
Curiosidades
Enlaces

Table of Contents

Introducción

Hace tiempo que me aficioné a los retos de Hacking y Cracking, y si bien la mayoría de ellos consisten en desencriptar una clave o realizar ingeniería inversa sobre un ejecutable, también los hay sobre programación pura y dura.

En esta ocasión se nos proporciona un código «muestra» parecido a PHP o C++ y tenemos que ingeniarnoslas para mejorarlo y ganar a la máquina.

Objetivo del juego y normas

El objetivo de esta misión es ganar a Tr0n en su propio juego: las carreras de motos. Se te proporcionará un programa (código) funcional para que veas como se controla el vehiculo. Usando tu inteligencia, tendrás que entender su uso y mejorarlo, ya que no es lo suficientemente bueno como para ganar a Tr0n. Tr0n lleva ya bastante tiempo en la parrilla de juegos y es bastante habilidoso 🙂

Cuando venzas a Tr0n un mínimo de 5 veces consecutivas, se te dará por superada esta prueba.

Buena suerte!!!

[ Available functions / Funciones disponibles ]
direction() returns current direction, change to a new one with direction([newdir])
getX(), getY() returns X and Y coordinates
collisionDistance() | collisionDistance([anydir]) returns the distance until collision
Note: parameters [*dir] can be empty or one of this values: UP DOWN LEFT or RIGHT

[ Constants / Constantes ]
UP DOWN LEFT RIGHT MAX_X MAX_Y

[ Rules / Reglas ]
Try to survive driving your bike and … / Intenta sobrevivir conduciendo tu moto y…
Don’t cross any line / No cruces ninguna línea
or crash with the corners! / o choques con las esquinas!

[ Mission / Mision ]
Use well this controller and beat Tr0n 5 consecutive times to score in this game
Usa bien este controlador y vence a Tr0n 5 veces consecutivas para puntuar en este juego

Código inicial

Nada más comenzar vemos que hemos perdido nuestra primera partida con el siguiente código:

	function controller(playerController $c){
		if($c->direction()==UP && $c->getY()<10){
			if(rand(0,1)==0) $c->direction(LEFT);
				else $c->direction(RIGHT);
			goto done;
		}
		if($c->direction()==DOWN && MAX_Y-$c->getY()<10){
			if(rand(0,1)==0) $c->direction(LEFT);
				else $c->direction(RIGHT);
			goto done;
		}
		if($c->direction()==LEFT && $c->getX()<10){
			if(rand(0,1)==0) $c->direction(UP);
				else $c->direction(DOWN);
			goto done;
		}
		if($c->direction()==RIGHT && MAX_X-$c->getX()<10){
			if(rand(0,1)==0) $c->direction(UP);
				else $c->direction(DOWN);
		}
		done:
	}

Nosotros somos el AZUL y la máquina es el VERDE.

Primeras modificaciones

Lo primero que tenemos que modificar son las distancias de las coordenadas que estan puestas en «<10» al mínimo, que sería «<2«. También sustituir la aleatoriedad «rand(0,1)==0» por algo más útil y comenzar a usar la función «collisionDistance()«.

Como podéis observar en el código inferior, usamos la función «collisionDistance()» para detectar cuando estamos a punto de chocar «collisionDistance() ==1» y para detectar a que lado nos conviene más girar en función de donde podamos recorrer más distancia «if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT); else $c->direction(RIGHT);«.

if($c->direction()==UP && $c->getY()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
		}
if($c->direction()==DOWN && MAX_Y-$c->getY()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
		}
if($c->direction()==LEFT && $c->getX()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) 
                                $c->direction(UP);
				else 
                                $c->direction(DOWN);
		}
if($c->direction()==RIGHT && MAX_X-$c->getX()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) $c->direction(UP);
				else $c->direction(DOWN);
				
		}

Terminando la faena

El código anterior de por sí no nos resuelve mucho si no afinamos un poco más, comprobando todos las posibles colisiones y tomando la dirección correcta en función de la mayor distancia a recorrer.

    if($c->collisionDistance([UP])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([DOWN])==1 || $c->collisionDistance() ==1){
            if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([RIGHT])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
     if($c->collisionDistance([LEFT])==1 || $c->collisionDistance() ==1){
          if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }

Código ganador

El código que utilicé yo para ganar a Tron es el siguiente:

function controller(playerController $c){
uno:
if($c->direction()==UP && $c->getY()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
				
		}
if($c->direction()==DOWN && MAX_Y-$c->getY()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([LEFT]) >2) $c->direction(LEFT);
				else $c->direction(RIGHT);
				
		}
if($c->direction()==LEFT && $c->getX()==1 && $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) 
                                $c->direction(UP);
				else 
                                $c->direction(DOWN);
				
		}
if($c->direction()==RIGHT && MAX_X-$c->getX()<2 || $c->collisionDistance() ==1){
			if($c->collisionDistance([UP]) >2) $c->direction(UP);
				else $c->direction(DOWN);
				
		}
dos:
    if($c->collisionDistance([UP])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([DOWN])==1 || $c->collisionDistance() ==1){
            if($c->collisionDistance([LEFT]) > $c->collisionDistance([RIGHT]))
               $c->direction(LEFT);
             else 
               $c->direction(RIGHT);
     }
     if($c->collisionDistance([RIGHT])==1 || $c->collisionDistance() ==1){
             if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
     if($c->collisionDistance([LEFT])==1 || $c->collisionDistance() ==1){
          if($c->collisionDistance([UP]) > $c->collisionDistance([DOWN]))
               $c->direction(UP);
             else 
               $c->direction(DOWN);
     }
		done:
	}

Mis jugadas ganadoras:

El código no es infalible ya que como comprabaréis vosotros mismos, no se puede ganar siempre por el mero hecho de la aleatoriedad y de la suerte. Cuando dispongais de un código decente, ejecutarlo varias veces para estar seguros antes de desecharlo.

Curiosidades

Como se suele decir, la banca siempre gana, y en este caso no iba a ser menos y es que en caso de empate ¡la banca gana!

Por último deciros que podéis utilizar el código ya que la web detecta los códigos ganadores para que no se repitan.

Enlaces

Web del reto

ai challenge deurus ia inteligencia artificial programación reto Tr0n tron Yoire

Los Pistoleros Solitarios

22 octubre, 2025 por deurus·Sin comentarios

En una entrada anterior sobre cómo Expediente X abordó la tecnología de vanguardia, comenté que dedicaría un espacio a esos tres personajes tan peculiares y entrañables que, desde el segundo plano, se ganaron un hueco en el corazón de los seguidores de la serie: los Pistoleros Solitarios. Pues bien, ha llegado el momento.

Estos tres tipos —John Fitzgerald Byers, Melvin Frohike y Richard “Ringo” Langly— no necesitaban armas ni placas del FBI. Su poder estaba en los teclados, los cables enredados y los monitores de tubo que parpadeaban en un sótano lleno de conspiraciones y café frío. Eran los outsiders de Expediente X, tres hackers con alma de periodistas que luchaban por algo tan simple y tan enorme como la verdad.

Su primera aparición fue en E.B.E. (temporada 1), casi como un alivio cómico: tres frikis que ayudaban a Mulder a rastrear información sobre ovnis. Pero pronto quedó claro que había algo especial en ellos. No solo eran fuente de datos, sino conciencia crítica en un mundo plagado de mentiras digitales y gobiernos con demasiados secretos. Con el tiempo se convirtieron en aliados imprescindibles de Mulder y Scully, y también en el reflejo más humano de lo que significa ser hacker: curiosos, testarudos, torpes a veces, pero con un sentido moral inquebrantable.

Byers era el idealista, el que aún creía en la decencia y en las instituciones (al menos en teoría). Frohike, el cínico veterano con corazón de oro, siempre dispuesto a arriesgarse por una buena causa… o por impresionar a Scully. Y Langly, el genio rebelde que parecía vivir en permanente conversación con su módem de 56 k. Juntos formaban un trío excéntrico, pero perfectamente equilibrado.

Mientras Mulder y Scully perseguían abducciones y virus extraterrestres, los pistoleros combatían en otra trinchera: la digital. Hackeaban redes gubernamentales, interceptaban comunicaciones cifradas y desmantelaban cortafuegos que, en los noventa, parecían pura ciencia ficción. Lo suyo no era la acción física, sino la resistencia informativa. Y aunque muchas veces eran el chiste del capítulo, también representaban algo muy real: la gente corriente que lucha contra el poder desde el conocimiento.

Su lema no declarado podría haber sido el clásico “la información quiere ser libre”, y en eso se mantuvieron firmes hasta el final. Si había que elegir entre la seguridad o la verdad, ellos siempre elegían la verdad, aunque les costara caro.

Temporada	Episodio	Título	Comentario
1	17	E.B.E.	Primera aparición de los pistoleros.
2	3	Blood	Manipulación de dispositivos y mensajes ocultos. También control mental a través de la tecnología.
2	25	Anasazi	Un hacker roba archivos clasificados. Se tratan temas como el cifrado y filtración de datos del gobierno.
3	15	Apocrypha	Acceso a bases de datos secretas y descifrado de archivos comprometidos.
3	23	Wetwired	Manipulación de señales televisivas.
4	14	Memento Mori	Infiltración digital en sistemas médicos y vigilancia biotecnológica.
5	1	Redux	Robo y manipulación de pruebas digitales.
5	3	Unusual Suspects	Orígenes de los pistoleros: intrusión, cifrado y espíritu hacker de los noventa.
5	11	Kill Switch	IA autónoma y malware inteligente.
6	20	Three of a Kind	Hacking social, suplantación y síntesis de voz para infiltración corporativa.
7	13	First Person Shooter	Hackeo de entornos virtuales y brechas de seguridad en sistemas de realidad aumentada.
9	15	Jump the Shark	Su sacrificio final: bloqueo de una amenaza biológica, ética hacker y altruismo extremo.
11	2	This	Langly como conciencia digital en un servidor. Debate sobre IA y trascendencia del código.

Morir por la verdad

El final de los pistoleros fue tan inesperado como heroico. En el episodio “Jump the Shark” de la novena temporada, descubren un complot bioterrorista que amenaza con liberar un virus mortal. No hay tiempo para avisar a nadie, ni margen para escapar. Así que, fieles a su estilo, deciden sacrificarse para salvar a otros. Sellan el laboratorio desde dentro, sabiendo que no volverán a salir.

Lo reconozco, este desenlace mi cogió completamente por sorpresa. No hay épica de Hollywood, ni música grandilocuente. Solo tres hombres anónimos haciendo lo correcto. Mueren juntos, sin reconocimiento, sin medallas, pero con la serenidad de quienes saben que su causa era justa. Y en ese silencio final, Expediente X nos recordó algo que las grandes historias suelen olvidar: que los verdaderos héroes a veces no llevan traje ni pistola, solo convicción.

Años después, Mulder vuelve a verlos —o cree verlos— en The Truth. Ya no están en este mundo, pero siguen a su lado, como fantasmas digitales de la conciencia hacker. Es un homenaje discreto a quienes siempre pelearon desde las sombras por liberar la verdad.

Para cerrar el círculo, Langly reaparece de forma inesperada en la temporada 11, dentro del episodio This. Su mente, o más bien su copia digital, sobrevive atrapada en un servidor, reclamando ser liberada. Es el epílogo perfecto: el hacker que muere físicamente, pero cuya conciencia sigue inmortal. Una vez más me volvió a sorprender Chris Carter con este homenaje.

Me gusta pensar que los pistoleros solitarios representaban algo más que tres hackers secundarios en una serie de los noventa. Fueron el reflejo de una época en la que creíamos que la tecnología podía liberar al ser humano, antes de que las redes sociales y la hiperconectividad lo diluyeran todo. Byers, Frohike y Langly no luchaban por fama ni por dinero: luchaban por entender el sistema para exponerlo, por esa curiosidad genuina que hoy apenas sobrevive entre líneas de código y algoritmos opacos. Quizá por eso seguimos recordándolos y mola tanto volver a ver los capítulos. Porque, de algún modo, todos los que amamos el conocimiento libre llevamos dentro un pequeño pistolero solitario, buscando la verdad entre los bits.

Expediente X Melvin Frohike mulder Pistoleros Solitarios scully x files

Migas de pan

4 agosto, 2024 por deurus·Sin comentarios

Se nos entrega el siguiente ELF:

/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
   Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>

   Detected compiler: GNU C++
*/

#include <defs.h>


//-------------------------------------------------------------------------
// Function declarations

__int64 (**init_proc())(void);
void sub_1020();
// int printf(const char *format, ...);
// int getchar(void);
// int fflush(FILE *stream);
// __int64 __isoc99_scanf(const char *, ...); weak
// void __noreturn exit(int status);
// int __fastcall _cxa_finalize(void *);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
FILE **deregister_tm_clones();
__int64 register_tm_clones(); // weak
FILE **_do_global_dtors_aux();
__int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD); // weak
int __fastcall main(int argc, const char **argv, const char **envp);
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3);
void _libc_csu_fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// int __fastcall __cxa_finalize(void *);
// __int64 _gmon_start__(void); weak

//-------------------------------------------------------------------------
// Data declarations

_UNKNOWN _libc_csu_init;
__int64 (__fastcall *_frame_dummy_init_array_entry)() = &frame_dummy; // weak
__int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)() = &_do_global_dtors_aux; // weak
void *_dso_handle = &_dso_handle; // idb
char *a = "MdfnJk"; // weak
char *b = "jYx}"; // weak
char *c = "gWmfk"; // weak
char *d = "mlvpc"; // weak
char *f = "neU++w"; // weak
FILE *_bss_start; // idb
char completed_0; // weak


//----- (0000000000001000) ----------------------------------------------------
__int64 (**init_proc())(void)
{
  __int64 (**result)(void); // rax

  result = &_gmon_start__;
  if ( &_gmon_start__ )
    return (__int64 (**)(void))_gmon_start__();
  return result;
}
// 40D0: using guessed type __int64 _gmon_start__(void);

//----- (0000000000001020) ----------------------------------------------------
void sub_1020()
{
  JUMPOUT(0LL);
}
// 1026: control flows out of bounds to 0

//----- (0000000000001090) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
  __int64 v3; // rax
  int v4; // esi
  __int64 v5; // [rsp-8h] [rbp-8h] BYREF
  char *retaddr; // [rsp+0h] [rbp+0h] BYREF

  v4 = v5;
  v5 = v3;
  _libc_start_main(
    (int (__fastcall *)(int, char **, char **))main,
    v4,
    &retaddr,
    (void (*)(void))_libc_csu_init,
    _libc_csu_fini,
    a3,
    &v5);
  __halt();
}
// 1096: positive sp value 8 has been found
// 109D: variable 'v3' is possibly undefined

//----- (00000000000010C0) ----------------------------------------------------
FILE **deregister_tm_clones()
{
  return &_bss_start;
}

//----- (00000000000010F0) ----------------------------------------------------
__int64 register_tm_clones()
{
  return 0LL;
}
// 10F0: using guessed type __int64 register_tm_clones();

//----- (0000000000001130) ----------------------------------------------------
FILE **_do_global_dtors_aux()
{
  FILE **result; // rax

  if ( !completed_0 )
  {
    if ( &__cxa_finalize )
      _cxa_finalize(_dso_handle);
    result = deregister_tm_clones();
    completed_0 = 1;
  }
  return result;
}
// 4080: using guessed type char completed_0;

//----- (0000000000001175) ----------------------------------------------------
int __fastcall main(int argc, const char **argv, const char **envp)
{
  char v4; // [rsp+7h] [rbp-9h] BYREF
  int v5; // [rsp+8h] [rbp-8h]
  bool v6; // [rsp+Fh] [rbp-1h]

  v6 = 1;
  v5 = 0;
  while ( v6 )
  {
    fflush(_bss_start);
    printf("\nIntroduce la letra correcta:\t");
    __isoc99_scanf("%c", &v4);
    getchar();
    if ( v5 > 5 )
    {
      if ( v5 > 9 )
      {
        if ( v5 > 14 )
        {
          if ( v5 > 19 )
            v6 = comprobacion(v4, f[v5 - 20], 10);
          else
            v6 = comprobacion(v4, d[v5 - 15], 2);
        }
        else
        {
          v6 = comprobacion(v4, c[v5 - 10], 8);
        }
      }
      else
      {
        v6 = comprobacion(v4, b[v5 - 6], 17);
      }
    }
    else
    {
      v6 = comprobacion(v4, a[v5], 5);
    }
    if ( !v6 )
    {
      printf("Incorrecta");
      exit(1);
    }
    printf("\n%c\n", (unsigned int)v4);
    if ( v5 == 25 )
    {
      printf("Ya tienes la flag!!");
      exit(1);
    }
    ++v5;
  }
  return 0;
}
// 1060: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 4050: using guessed type char *a;
// 4058: using guessed type char *b;
// 4060: using guessed type char *c;
// 4068: using guessed type char *d;
// 4070: using guessed type char *f;

//----- (0000000000001352) ----------------------------------------------------
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3)
{
  return a1 == (a3 ^ a2);
}

//----- (0000000000001390) ----------------------------------------------------
void __fastcall _libc_csu_init(unsigned int a1, __int64 a2, __int64 a3)
{
  signed __int64 v4; // rbp
  __int64 i; // rbx

  init_proc();
  v4 = &_do_global_dtors_aux_fini_array_entry - &_frame_dummy_init_array_entry;
  if ( v4 )
  {
    for ( i = 0LL; i != v4; ++i )
      ((void (__fastcall *)(_QWORD, __int64, __int64))*(&_frame_dummy_init_array_entry + i))(a1, a2, a3);
  }
}
// 1170: using guessed type __int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD);
// 3DE8: using guessed type __int64 (__fastcall *_frame_dummy_init_array_entry)();
// 3DF0: using guessed type __int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)();

//----- (00000000000013F4) ----------------------------------------------------
void term_proc()
{
  ;
}

Extracción de la Flag

Si nos fijamos en las líneas 41 a la 45 vemos las siguientes cadenas:

a = «MdfnJk»
b = «jYx}»
c = «gWmfk»
d = «mlvpc»
f = «neU++w»

Usaremos las cadenas y los valores XOR especificados para cada rango de v5 en el main (líneas 123 a 182) para determinar los caracteres correctos.

Para v5 de 0 a 5: v6 = comprobacion(v4, a[v5], 5);
Significa que: v4 debe ser igual a a[v5] ^ 5

Para v5 de 6 a 9: v6 = comprobacion(v4, b[v5 – 6], 17);
Significa que: v4 debe ser igual a b[v5 – 6] ^ 17

Para v5 de 10 a 14: v6 = comprobacion(v4, c[v5 – 10], 8);
Significa que: v4 debe ser igual a c[v5 – 10] ^ 8

Para v5 de 15 a 19: v6 = comprobacion(v4, d[v5 – 15], 2);
Significa que: v4 debe ser igual a d[v5 – 15] ^ 2

Para v5 de 20 a 25: v6 = comprobacion(v4, f[v5 – 20], 10);
Significa que: v4 debe ser igual a f[v5 – 20] ^ 10

Cálculo de los caracteres correctos:
Para v5 de 0 a 5:
a[0] = ‘M’, M ^ 5 = 0x4D ^ 0x05 = 0x48 -> ‘H’
a[1] = ‘d’, d ^ 5 = 0x64 ^ 0x05 = 0x61 -> ‘a’
a[2] = ‘f’, f ^ 5 = 0x66 ^ 0x05 = 0x63 -> ‘c’
a[3] = ‘n’, n ^ 5 = 0x6E ^ 0x05 = 0x6B -> ‘k’
a[4] = ‘J’, J ^ 5 = 0x4A ^ 0x05 = 0x4F -> ‘O’
a[5] = ‘k’, k ^ 5 = 0x6B ^ 0x05 = 0x6E -> ‘n’
Resulta en la cadena: HackOn

Para v5 de 6 a 9:
b[0] = ‘j’, j ^ 17 = 0x6A ^ 0x11 = 0x7B -> ‘{‘
b[1] = ‘Y’, Y ^ 17 = 0x59 ^ 0x11 = 0x48 -> ‘H’
b[2] = ‘x’, x ^ 17 = 0x78 ^ 0x11 = 0x69 -> ‘i’
b[3] = ‘}’, } ^ 17 = 0x7D ^ 0x11 = 0x6C -> ‘l’
Resulta en la cadena: {Hil

Para v5 de 10 a 14:
c[0] = ‘g’, g ^ 8 = 0x67 ^ 0x08 = 0x6F -> ‘o’
c[1] = ‘W’, W ^ 8 = 0x57 ^ 0x08 = 0x5F -> ‘_’
c[2] = ‘m’, m ^ 8 = 0x6D ^ 0x08 = 0x65 -> ‘e’
c[3] = ‘f’, f ^ 8 = 0x66 ^ 0x08 = 0x6E -> ‘n’
c[4] = ‘k’, k ^ 8 = 0x6B ^ 0x08 = 0x63 -> ‘c’
Resulta en la cadena: o_enc

Para v5 de 15 a 19:
d[0] = ‘m’, m ^ 2 = 0x6D ^ 0x02 = 0x6F -> ‘o’
d[1] = ‘l’, l ^ 2 = 0x6C ^ 0x02 = 0x6E -> ‘n’
d[2] = ‘v’, v ^ 2 = 0x76 ^ 0x02 = 0x74 -> ‘t’
d[3] = ‘p’, p ^ 2 = 0x70 ^ 0x02 = 0x72 -> ‘r’
d[4] = ‘c’, c ^ 2 = 0x63 ^ 0x02 = 0x61 -> ‘a’
Resulta en la cadena: ontra

Para v5 de 20 a 25:
f[0] = ‘n’, n ^ 10 = 0x6E ^ 0x0A = 0x64 -> ‘d’
f[1] = ‘e’, e ^ 10 = 0x65 ^ 0x0A = 0x6F -> ‘o’
f[2] = ‘U’, U ^ 10 = 0x55 ^ 0x0A = 0x5F -> ‘_‘
f[3] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[4] = ‘+’, + ^ 10 = 0x2B ^ 0x0A = 0x21 -> ‘!’
f[5] = ‘w’, w ^ 10 = 0x77 ^ 0x0A = 0x7D -> ‘}’
Resulta en la cadena: do_!!}

Uniendo todas las partes, obtenemos la flag completa: HackOn{Hilo_enc_ontrado_!!}

challenge crackme dogbolt.org ELF reto

Mirror Crackmes.de

29 marzo, 2017 por deurus·Sin comentarios

~~While Crackmes.de returns, I leave a couple of files for practice.~~

~~Mientras vuelve Crackmes.de, os dejo un par de archivos para practicar.~~

~~In the folder crackmes.de_mirror you have two files:~~

~~En la carpeta crackmes.de_mirror tienes dos archivos:~~

~~Crackmes.de (2011 – 2015).rar [491 MB] [password: tuts4you]~~
~~crackmes.de-2016-12.7z [639 MB]~~

 password of files = deurus.info

Solución a los retos javascript de rogerfm.net

Introducción Javascript 1 (Serial a la vista) Javascript 2 (La función charAt()) Javascript 3 (Input) Javascript 4 (Fuerza bruta manual) Javascript

Keygen para el Crackme Sweeet Dream 1.0 de 2Sweeet

Intro Hoy tenemos aquí un crackme del año 2000 empacado y con un algoritmo aunque no muy complicado largo de

Yoire PE Reversing Challenge (Crackme Very Hard)

Aviso: Este crackme forma parte de una serie de pruebas de Yoire.com que todavía está en activo. Lo ético si

Solución a los retos criptográficos de Rogerfm.net

Introducción Cripto 1 Cripto 2 Cripto 3 Cripto 4 Cripto 5 Cripto 6 Cripto 7 Cripto 8 Cripto 9 Cripto 10

1 2 3 … 30 Next »

javascript

Solución a los retos javascript de rogerfm.net

30 septiembre, 2016 por deurus·Sin comentarios

Introducción
Javascript 1 (Serial a la vista)
Javascript 2 (La función charAt())
Javascript 3 (Input)
Javascript 4 (Fuerza bruta manual)
Javascript 5 (Fuerza bruta)
Enlaces

Table of Contents

Introducción

Los retos de Javascript son los retos más sencillos que podemos encontrar. Muchas veces solamente mirando el código fuente obtenemos la respuesta. Suponen una mala implementación de seguridad debido a que el código se ejecuta del lado del cliente, por lo que el código fuente es accesible y por lo tanto, javascript no garantiza seguridad alguna. En estos cinco casos haremos un recorrido por lo más básico, cinco retos fáciles de superar y que nos proporcionan los conocimientos base para Javascript. Dicho esto os puedo asegurar que en ocasiones he encontrado retos javascript realmente complicados que requieren de horas descifrarlos y en los que es fácil tirar la toalla.

Cuando el reto lo requiera, es buena idea utilizar un compilador online para obtener de forma rápida el valor de una variable o realizar una prueba concreta. Yo utilizo Jsfiddle para realizar pruebas pero existen muchos más.

Javascript 1

Este primer reto es lo básico, en el código fuente se pueden apreciar directamente el usuario y la clave.

<script language=JavaScript>
function Verify(name,pass)
{
if (name=="admin" & pass=="3***3")
	{
	location.href = name + pass + '.htm';
	}
else 
	{
	alert("Si ya fallamos el primero...");
	};
}
</script>

Javascript 2

Este segundo reto es bastante sencillo pero ya te obliga a conocer la función charAt() de Javascript. Dicha función lo que hace es coger el caracter indicado mediante un índice que comienza en cero. Por ejemplo si nombre = deurus y hacemos letra = nombre.charAt(3), estariámos extrayendo la cuarta letra, es decir, la letra r de la variable nombre.

function Verify(name,pass)
{
var name1 = "CrawlinG", pass1 = "capriccio"
	if (name==name1 & pass==pass1)
	{
	location.href = name + ".htm";
	}
else 
	{
	var x =  name1.charAt(7) + pass1.charAt(3)+ name1.charAt(2) + pass1.charAt(5) +  name1.charAt(5) + pass1.charAt(1);x = x.toLowerCase();
	var y =  name.charAt(3) + name.charAt(1) + pass.charAt(1)+ pass.charAt(6) +  pass.charAt(7) + name.charAt(2);var x1 = "des" + y;
	if (x==y){location.href = x1 + ".htm"}else{alert("Esto no va bien");location.href = "js2.htm"}
	}
}

Lo interesante está en la formación de las variables x e y. La variable x se forma de las variables name1 y pass1, formando la palabra gracia. Por otro lado, la variable y se forma con el nombre y clave que introduzcamos nosotros. Vemos que la variable x e y deben ser iguales, por lo tanto debemos construir un nombre (name) y una clave (pass) que cumpla con lo siguiente:

4ª letra del nombre = 1ª letra de la palabra «gracia»
2ª letra del nombre = 2ª letra de la palabra «gracia»
2ª letra de la clave = 3ª letra de la palabra «gracia»
7ª letra de la clave = 4ª letra de la palabra «gracia»
8ª letra de la clave = 5ª letra de la palabra «gracia»
3ª letra del nombre = 6ª letra de la palabra «gracia«

Como véis simplemente se trata de interpretar correctamente la función charAt() y de fijarse bien en los nombres de las variables.

Javascript 3

Este reto nos muestra diálogo donde nos pide la contraseña para validar el reto. Al fallar o cancelar vuelve al índice para no dejarnos ver el código fuente. Aquí se pueden seguir varios caminos como bloquear el uso de javascript en el navegador o instalar un plugin en chrome o firefox para habilitar/deshabilitar de forma rápida el uso de javascript.

Una vez deshabilitado javascript vemos lo siguiente:

<script language="JavaScript" src="js3.gif" type=text/javascript>
<!--
function verify()
{
var pass="thebest";
var password=prompt("Introduce el password para superar el nivel","");
	if (password==pass)
		{
		location.href = pass + ".htm";
		}
	else
		{
		alert("No vamos bien...");
		location.href = "index.htm";
		}
}
//-->
</script>

Aquí el truco es darse cuenta que el código que se está ejecutando esta en «js3.gif» y no el código que nos muestra como válida la clave thebest. Si descargamos el archivo js3.gif y lo abrimos con un archivo de texto vemos nuestra querida clave.

function verify()
{
var pass="mo****ver";
var password=prompt("Introduce el password para superar el nivel","");
	if (password==pass)
		{
		location.href = pass + ".htm";
		}
	else
		{
		alert("No vamos bien...");
		location.href = "index.htm";
		}
}

Javascript 4

En este reto ya entramos con que la clave no es reversible y la debemos obtener por fuerza bruta. En este reto utiliza una nueva función como charCodeAt() que lo que hace es obtener el valor ascii del caracter indicado.

function Verify(pass1)
{
var cont1= 2, cont2= 6
var suma1 = 0, suma2 = 0
var pass2 = "FDRLF"
for(i = 0; i < pass1.length; i++) 
{
suma1 += (pass1.charCodeAt(i) * cont1);
cont1++
}
for(i = 0; i < pass2.length; i++) 
{
suma2 += (pass2.charCodeAt(i) * cont2);
cont2++
}
if (suma1==suma2)
{
window.location=suma1+".htm";
}
else
{
alert ("Algo no va bien...");
}
}

Vemos dos bucles en los que se calculan sendos valores suma que finalmente se comparan. la variable suma1 se calcula mediante nuestro password y la variable suma2 la obtiene de la palabra «FDRLF». Con el script que os muestro a continuación obtenemos que usando como clave deurus, suma1 = 3048 y suma2 = 2936. Nuestro punto de referencia es suma2 = 2936, de modo que vamos alterando con paciencia la variable pass1 obteniendo valores cercanos a 2936. Por ejemplo «deurua» nos da suma1 = 2922, un valor bastante cercano.

var pass1 = "deurus";
var cont1= 2, cont2= 6
var suma1 = 0, suma2 = 0
var pass2 = "FDRLF"
for(i = 0; i < pass1.length; i++) 
{
suma1 += (pass1.charCodeAt(i) * cont1);
cont1++
}
for(i = 0; i < pass2.length; i++) 
{
suma2 += (pass2.charCodeAt(i) * cont2);
cont2++
}
alert (suma1);
alert (suma2);

La solución a este reto es múltiple. Dos claves válidas son por ejemplo dfurqf y zwfabz.

Javascript 5

Este último reto es similar al anterior pero ya nos obliga a crearnos una pequeña herramienta que nos busque el serial válido.

function Verify(pass)
{
var suma=0
var cadena = "abcdefghijklmnopqrstuvwxyz"
for (var i = 0; i < pass.length; i++) 
	{
	var letra = pass.charAt(i)
	var valor = (cadena.indexOf(letra))
	valor++
	suma *= 26
	suma += valor
	}
if (suma==6030912063)
	{
	window.location=pass+".htm";
	}
else
	{
	alert ("Algo no va bien...");
	}
}

Para esta ocasión utiliza una nueva función llamada indexOf() que lo que hace es devolver un número entero que representa la posición en la que se encuentra el parámetro pasado a la función. Por ejemplo, si tengo variable = deurus y realizo posición = variable.indexOf(«s»), obtengo como resultado 5 (se empieza a contar desde cero).

Las operaciones que realiza el bucle son las siguientes:

Coge las letras del nombre una a una.
valor = posición de nuestra letra dentro de la variable de texto llamada cadena.
valor = valor + 1.
Multiplica la variable suma por 26.
Suma = suma + valor.

Aunque el proceso de recuperación de esta clave es algo más largo, podemos acortarlo introduciendo una clave de inicio de fuerza bruta próxima al objetivo. Al ser una función bastante lineal podemos rápidamente mediante pruebas con nuestro código de fuerza bruta o con un compilador online, establecer que la clave tendrá 7 caracteres e incluso que para ahorrar tiempo podemos aproximar la clave para que su valor suma esté cercano al valor suma buscado 6030912063.

Realizando pruebas obtenemos:

Clave = aaaaaaa -> suma = 321272407
Clave = zzzzzzz -> suma = 8353082582
Clave = smaaaaa -> suma = 6024332887
Clave = smkkkkk -> suma = 6029085437

Como vemos, la clave smkkkkk ya está bastante próxima al objetivo y será un buen punto para lanzar la fuerza bruta.

Os dejo el código de fuerza bruta en .Net

Module Module1
    Sub Main()
inicio:
        Console.WriteLine("-------------------------")
        Console.WriteLine("Modo [1] Prueba password")
        Console.WriteLine("Modo [2] Fuerza bruta")
        Console.WriteLine("-------------------------")
        Dim modo = Console.ReadLine()
        '
        If modo = 2 Then
            Console.WriteLine("¿Password para comenzar?")
            Dim pass = Console.ReadLine()
inicio2:
            Dim cadena As String = "abcdefghijklmnopqrstuvwxyz"
            Dim valor As Integer = 0
            Dim suma As Long = 0
            Dim letra As String
            For i = 0 To pass.Length - 1
                letra = Mid(pass, i + 1, 1)
                valor = cadena.IndexOf(letra)
                valor += 1
                suma *= 26
                suma += valor
            Next
            Console.WriteLine("Password: " & pass & " - Sum: " & suma.ToString)
            pass = IncrementString(pass)
            If suma = 6030912063 Then
                MsgBox("Password is " & pass)
            Else
                If pass = "aaaaaaaa" Then
                    Console.WriteLine("pass not found")
                    Console.ReadKey()
                Else
                    GoTo inicio2
                End If
            End If
        End If
        '------------------------------------------------
        If modo = 1 Then
            Console.WriteLine("Password:")
            Dim pass = Console.ReadLine()
            Dim cadena As String = "abcdefghijklmnopqrstuvwxyz"
            Dim valor As Integer = 0
            Dim suma As Long = 0
            Dim letra As String
            For i = 0 To pass.Length - 1
                letra = Mid(pass, i + 1, 1)
                valor = cadena.IndexOf(letra)
                valor += 1
                suma *= 26
                suma += valor
            Next
            Console.WriteLine("Password: " & pass & " - Sum: " & suma.ToString)
            Console.WriteLine(".......")
            Console.WriteLine("Good = 6030912063")
            Console.WriteLine("Suma = " & suma.ToString)
            Console.ReadKey()
            Console.Clear()
            GoTo inicio
        End If
    End Sub
    Function IncrementString(ByVal strString As String) As String
        '
        ' Increments a string counter
        ' e.g.  "a" -> "b"
        '       "az" -> "ba"
        '       "zzz" -> "aaaa"
        '
        ' strString is the string to increment, assumed to be lower-case alphabetic
        ' Return value is the incremented string
        '
        Dim lngLenString As Long
        Dim strChar As String
        Dim lngI As Long

        lngLenString = Len(strString)
        ' Start at far right
        For lngI = lngLenString To 0 Step -1
            ' If we reach the far left then add an A and exit
            If lngI = 0 Then
                strString = "a" & strString
                Exit For
            End If
            ' Consider next character
            strChar = Mid(strString, lngI, 1)
            If strChar = "z" Then
                ' If we find Z then increment this to A
                ' and increment the character after this (in next loop iteration)
                strString = Left$(strString, lngI - 1) & "a" & Mid(strString, lngI + 1, lngLenString)
            Else
                ' Increment this non-Z and exit
                strString = Left$(strString, lngI - 1) & Chr(Asc(strChar) + 1) & Mid(strString, lngI + 1, lngLenString)
                Exit For
            End If
        Next lngI
        IncrementString = strString
        Exit Function

    End Function
End Module

Enlaces

Web del reto
Jsfiddle (compilador online)

javascript

Keygen para el Crackme Sweeet Dream 1.0 de 2Sweeet

27 septiembre, 2014 por deurus·Sin comentarios

Intro

Hoy tenemos aquí un crackme del año 2000 empacado y con un algoritmo aunque no muy complicado largo de tracear. Está empacado varias veces, algo poco habitual pero recordemos que es un crackme antiguo. Tras el empacado se encuentra Delphi.

Herramientas

PEiD o similar.
OllyDbg con plugin OllyDumpEX.
Import REConstructor.
LordPE (Opcional).

Desempacado multicapa

VideoTutorial del desempacado disponible

Si lo pasamos por PEiD nos dice que Aspack 2.1, Exeinfo no está muy seguro y RDG packer detector en el escaneo avanzado nos encuentra Aspack, UPX y PE-Pack.

En principio nos enfrentamos a Aspack 2.1, abrimos el crackme con OllyDbg y vemos el típico PUSHAD.

Pulsamos F8 (Step Over) y a continuación click derecho sobre el registro ESP y Follow in DUMP.

Seleccionamos los primeros cuatro bytes útiles del dump y les ponemos un Breakpoint de Hardware, Access y Dword.

Pulsamos F9 y nos para aquí:

Ya tenemos a Aspack contra las cuerdas, pulsamos F8 hasta después del RETN para llegar al OEP (Original Entry Point).

Pero en el supuesto OEP vemos otro PUSHAD por lo que esto no ha terminado. Investigando un poco más vemos que la segunda capa se corresponde con PE-PACK 1.0. La estrategia a seguir es la misma, como ya tenemos el breakpoint puesto pulsamos F9 y nos para aquí:

Pulsamos F8 y nos llega a otro PUSHAD. Esta vez es UPX.

Pulsamos de nuevo F9 y paramos aquí:

Pulsamos F8 y esta vez si llegamos al OEP (4576EC).

A continuación vamos a dumpear el archivo en memoria. Vamos a plugins > OllyDumpEX, pulsamos sobre «Get EIP as OEP» y finalmente sobre «Dump«.

Minimizamos Olly (no cerrar), abrimos el programa ImportREC y seleccionamos el ejecutable «Sweeet1.exe».

Pegamos el OEP original (576EC), le damos a AutoSearch y a continuación a Get Imports.

Finalmente pulsamos Fix Dump y elegimos el ejecutable dumpeado anteriormente. Esto nos genera un ejecutable dumpeado que es el ejecutable válido.

Ahora PEiD nos dice que estamos tratando con un crackme hecho en Delphi.

Hemos pasado por tres capas de compresión casi idénticas, vamos a analizarlas.

El algoritmo

Cuando abrimos el crackme nos fijamos en que genera una key. Esta key se genera en función del disco duro desde el que se ejecuta.

Como la secuencia de generación del serial válido es larga os pongo lo más importante muy resumido y con ejemplos como siempre.

El serial es del siguiente tipo:

Serial = 1ªParte-2ªParte-3ªParte
Serial = 0000XXXXX-SerialCalculado-xxxx000Z8

Comprobación del tamaño del nombre
----------------------------------
........
00456EAA    E8 01CCFAFF     CALL sweeet1_Fix_dump_rebuilded.00403AB0
00456EAF    83F8 04         CMP EAX,4    ------------------------------------------------; Nombre >=4                    
00456EB2    7D 13           JGE SHORT sweeet1_Fix_dump_rebuilded.00456EC7
00456EB4    A1 08954500     MOV EAX,DWORD PTR DS:[sweeet1_Fix_dump_rebuilded.459508]
00456EB9    8B00            MOV EAX,DWORD PTR DS:[EAX]
00456EBB    E8 0869FEFF     CALL sweeet1_Fix_dump_rebuilded.0043D7C8
00456EC0    BB 01000000     MOV EBX,1
00456EC5    EB 15           JMP SHORT sweeet1_Fix_dump_rebuilded.00456EDC
00456EC7    83FB 25         CMP EBX,25                                                                                                
00456ECA    7D 0E           JGE SHORT sweeet1_Fix_dump_rebuilded.00456EDA
00456ECC    83C3 32         ADD EBX,32
00456ECF    83C3 1E         ADD EBX,1E
00456ED2    83EB 4F         SUB EBX,4F
00456ED5    83FB 25         CMP EBX,25 -----------------------------------------------; Nombre <=25
00456ED8  ^ 7C F2           JL SHORT sweeet1_Fix_dump_rebuilded.00456ECC
00456EDA    33DB            XOR EBX,EBX
00456EDC    33C0            XOR EAX,EAX
........

1ºBucle - Nuestro nombre (A)
----------------------------
........
00456F55    BE 1B000000     MOV ESI,1B -------------------------------; ESI = 1B
00456F5A    EB 21           JMP SHORT sweeet1_dump_.00456F7D
00456F5C    8D55 D4         LEA EDX,[EBP-2C]
00456F5F    A1 34A84500     MOV EAX,DWORD PTR DS:[sweeet1_dump_.45A8
00456F64    8B80 C4020000   MOV EAX,DWORD PTR DS:[EAX+2C4]
00456F6A    E8 B5DAFCFF     CALL sweeet1_dump_.00424A24
00456F6F    8B45 D4         MOV EAX,DWORD PTR SS:[EBP-2C]
00456F72    0FB64418 FF     MOVZX EAX,BYTE PTR DS:[EBX+EAX-1]---------; Coje digito
00456F77    03F0            ADD ESI,EAX ------------------------------; digito + ESI
00456F79    43              INC EBX
00456F7A    0FAFF3          IMUL ESI,EBX  ----------------------------; multiplica por i (bucle)
00456F7D    8D55 D4         LEA EDX,[EBP-2C]
........

2ºBucle - La key (B)
--------------------
........
00456F9C         |.  BF 1A000000            MOV EDI,1A -------------------------;EDI = 1A
00456FA1         |.  BB 01000000            MOV EBX,1
00456FA6         |.  EB 1E                  JMP SHORT sweeet1_.00456FC6
00456FA8         |>  8D55 D4                /LEA EDX,[LOCAL.11]
00456FAB         |.  A1 34A84500            |MOV EAX,DWORD PTR DS:[45A834]
00456FB0         |.  8B80 D0020000          |MOV EAX,DWORD PTR DS:[EAX+2D0]
00456FB6         |.  E8 69DAFCFF            |CALL sweeet1_.00424A24
00456FBB         |.  8B45 D4                |MOV EAX,[LOCAL.11]
00456FBE         |.  0FB64418 FF            |MOVZX EAX,BYTE PTR DS:[EAX+EBX-1]--;Coje dígito
00456FC3         |.  03F8                   |ADD EDI,EAX -----------------------;Suma dígito a dígito
00456FC5         |.  43                     |INC EBX
00456FC6         |>  8D55 D4                 LEA EDX,[LOCAL.11]
00456FC9         |.  A1 34A84500            |MOV EAX,DWORD PTR DS:[45A834]
00456FCE         |.  8B80 D0020000          |MOV EAX,DWORD PTR DS:[EAX+2D0]
00456FD4         |.  E8 4BDAFCFF            |CALL sweeet1_.00424A24
00456FD9         |.  8B45 D4                |MOV EAX,[LOCAL.11]
00456FDC         |.  E8 CFCAFAFF            |CALL sweeet1_.00403AB0
00456FE1         |.  3BD8                   |CMP EBX,EAX
00456FE3         |.^ 7C C3                  \JL SHORT sweeet1_.00456FA8
........

Generación del serial central
-----------------------------
........
00456FE5         |.  B9 01000000            MOV ECX,1
00456FEA         |.  BB 01000000            MOV EBX,1
00456FEF         |.  8BC7                   MOV EAX,EDI
00456FF1         |.  F7EE                   IMUL ESI ----------; C = A * B
00456FF3         |.  99                     CDQ
........
00456FFD         |.  2345 E8                AND EAX,[LOCAL.6]--; D = A and C
00457000         |.  2355 EC                AND EDX,[LOCAL.5]
00457003         |.  8945 E8                MOV [LOCAL.6],EAX
00457006         |.  8955 EC                MOV [LOCAL.5],EDX
........
00457032         |.  8BC7                   MOV EAX,EDI
00457034         |.  99                     CDQ
00457035         |.  0345 E8                ADD EAX,[LOCAL.6]--; E = D + B
00457038         |.  1355 EC                ADC EDX,[LOCAL.5]
0045703B         |.  8945 E0                MOV [LOCAL.8],EAX
0045703E         |.  8955 E4                MOV [LOCAL.7],EDX
........
00405732           8B4424 10                MOV EAX,DWORD PTR SS:[ESP+10]
00405736           F72424                   MUL DWORD PTR SS:[ESP]
00405739           8BC8                     MOV ECX,EAX
0040573B           8B4424 04                MOV EAX,DWORD PTR SS:[ESP+4]
0040573F           F76424 0C                MUL DWORD PTR SS:[ESP+C]------; F = B * D
00405743           03C8                     ADD ECX,EAX
00405745           8B0424                   MOV EAX,DWORD PTR SS:[ESP]
00405748           F76424 0C                MUL DWORD PTR SS:[ESP+C]------; G = A * F
........
0045705E         |.  0B0424                 OR EAX,DWORD PTR SS:[ESP]-----; Serial central = G or A
........
00457077         |.  E8 FC07FBFF            CALL sweeet1_.00407878
0045707C         |.  8B45 F8                MOV EAX,[LOCAL.2]-------------; EAX = Serial central
........
004570D1         |.  E8 A207FBFF            CALL sweeet1_.00407878
004570D6         |.  8B45 D0                MOV EAX,[LOCAL.12]
004570D9         |.  E8 D2C9FAFF            CALL sweeet1_.00403AB0--------; Obtiene longitud del serial central en hexa
004570DE         |.  8BD8                   MOV EBX,EAX
........
004570D1         |.  E8 A207FBFF            CALL sweeet1_.00407878--------;*Nota

*Nota:
A partir de aquí genera la primera y tercera parte del serial de la siguiente manera:

Serial = 1ªParte-2ªParte-3ªParte
Serial = 0000XXXXX-SerialCalculado-xxxx000Z8

1ºParte = 3ºdigSerial+1ºdigSerial+2ºdigSerial+3ºdigSerial+4ºdigNombreMayu+2ºdigNombreMayu+5ºdigNombreMayu+1ºdigNombreMayu+3ºdigNombreMayu
3ºParte = 3ºdigNombreMin+1ºdigNombreMin+4ºdigNombreMin+2ºdigNombreMin+Tamaño Serial_2ªParte en Hex y de tres dígitos+Z8

Ejemplo:

Nombre: deurus
Key:    C0C0A000
Serial: 6906REUDU-906297047918-udre00CZ8

1) A = 23A2A (Con nuestro nombre empezando por 1B se lo suma a ESI y se lo multiplica por i (la que toque cada vez))
2) B = 1A1 (Con nuestra Key empezando por 1A va sumando los digitos)
3) C = B * A = 3A0BE6A
4) D = A and C = 3A2A
5) E = D + B = 3BCB (Offset 457035)
6) F = B * D = 5EBE6A (Offset 48704A)
7) G = A * F = D303834164
8) Serial = G or A (Serial = D303834164 or 23A2A = D303837B6E (906297047918))

A tener en cuenta:

1ªParte del serial siempre mayúsculas.
2ªParte siempre numérico. Usa el registro de 64 bits (Qword) con signo.**Nota
3ªParte siempre minúsculas.

**Nota:

Nombre: deurus.info
Key:    E09FF000
Serial: 9169REUDU-16918236-udre008Z8

Fíjate que: -16918236 = FFFFFFFFFEFDD924

Nombre: deurus
Key:    C0C0A000
Serial: 6906REUDU-906297047918-udre00CZ8

906297047918 = 000000D303837B6E

Links

Andy's Keygenme Keygen (AutoIt)

Introducción Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro

Reto forense "Find the cat" de Root-Me.org

Intro President’s cat was kidnapped by separatists. A suspect carrying a USB key has been arrested. Berthier, once again, up

ThisIsLegal.com - Realistic Challenge 4

Warning: This challenge is still active and therefore should not be resolved using this information. Aviso: Este reto sigue en

Crypto - Vodka

Hemos interceptado un mensaje secreto, pero ninguno de nuestros traductores lo sabe interpretar, ¿sabrías interpretarlo tú? Lo único que hemos

1 2 3 … 30 Next »

crackme Crackmes.de deurus Keygen

Andy’s Keygenme Keygen (AutoIt)

2 septiembre, 2014 por deurus·Sin comentarios

Introducción

Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro keygen. Como comprobareis si no se ofusca o se toman otro tipo de medidas recuperar información sensible es muy sencillo.

AutoIt es un lenguaje freeware multiproposito y de automatización para Microsoft Windows. Es un Visual Basic Killer, ya que mejora las características de los ejecutables (entre otras portabilidad, velocidad y peso, no fat-coding), y facilitan la programación con un buen repertorio de funciones «pre-diseñadas», y usando un Basic de fácil aprendizaje. Se ha expandido desde sus comienzos de automatización incluyendo muchas mejoras en el diseño del lenguaje de programación y sobre todo en nuevas funcionalidades.

El Script

Func CHECKKEY($USER, $PASS)
Local $OPKEY = "", $SIG = ""
Local $USER_LEN = StringLen($USER)
Local $PASS_LEN = StringLen($PASS)
If $USER_LEN < $PASS_LEN Then
MsgBox(0, "ERROR", "Invalid username or key.")
Exit
ElseIf $USER_LEN < 4 Then
MsgBox(0, "ERROR", "Invalid username or key.")
Exit
EndIf
$PASS_INT = Int($USER_LEN / $PASS_LEN)
$PASS_MOD = Mod($USER_LEN, $PASS_LEN)
$OPKEY = _STRINGREPEAT($PASS, $PASS_INT) & StringLeft($PASS, $PASS_MOD)
For $INDEX = 1 To $USER_LEN
$SIG &= Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), Asc(StringMid($OPKEY, $USER_LEN - $INDEX + 1, 1))))
Next
If $SIG = _STRINGREPEAT(Chr(32), $USER_LEN) Then
MsgBox(0, "INFO", "Your key was registered.")
Exit
Else
MsgBox(0, "INFO", "Your key is invalid.")
EndIf
EndFunc

El Algoritmo

El algoritmo es tremendamente sencillo ya que es nuestro nombre al revés y en mayúsculas.

Modificando el script para generar nuestro propio keygen

El decompilador se llama myAut2exe y tiene este aspecto.

Programar en AutoIt es muy sencillo e intuitivo. Nuestro keygen quedaría así.

$MAIN = GUICreate("Another keygen by deurus", 300, 80, -1, -1, 382205952, 385)
$NAME_LBL = GUICtrlCreateLabel("Username", 5, 5, 60, 20, BitOR(4096, 1))
$NAME_INP = GUICtrlCreateInput("", 70, 5, 225, 20, 1)
$PASS_LBL = GUICtrlCreateLabel("Key", 5, 30, 60, 20, BitOR(4096, 1))
$PASS_INP = GUICtrlCreateInput("", 70, 30, 225, 20, 1)
$REGISTER = GUICtrlCreateButton("Register", 5, 55, 60, 20)
$GIVE_UP = GUICtrlCreateButton("Generate", 70, 55, 60, 20)    <- Change name of button, Give Up by Generate
$TASK = GUICtrlCreateButton("?", 140, 55, 20, 20)
$AUTHOR = GUICtrlCreateLabel("keygen by deurus", 165, 55, 130, 20, BitOR(4096, 1))
GUISetState(@SW_SHOW, $MAIN)
While True
    $MSG = GUIGetMsg()
    Switch $MSG
        Case $REGISTER
            Call("CHECKKEY", GUICtrlRead($NAME_INP), GUICtrlRead($PASS_INP))
        Case $GIVE_UP
            Call("GETKEY", GUICtrlRead($NAME_INP), GUICtrlRead($PASS_INP))    <- Add the function to the button
        Case $TASK
            MsgBox(0, "Info", "keygen by deurus")
        Case - 3
            Exit
    EndSwitch
    Sleep(15)
WEnd

Func GETKEY($USER, $PASS)        <- this is our keygen function
    Local $OPKEY = "", $SIG = ""
    Local $USER_LEN = StringLen($USER)
    Local $PASS_LEN = StringLen($USER)
    If $USER_LEN < 4 Then
        GUICtrlSetData($PASS_INP  ,"min 4 chars");
    Else
    For $INDEX = 1 To $USER_LEN
        $SIG = Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), 32)) & $SIG
    Next
        GUICtrlSetData($PASS_INP  ,$SIG);
    EndIf
EndFunc

Func CHECKKEY($USER, $PASS)        <- check function, the original
    Local $OPKEY = "", $SIG = ""
    Local $USER_LEN = StringLen($USER)
    Local $PASS_LEN = StringLen($PASS)
    If $USER_LEN < $PASS_LEN Then
        MsgBox(0, "ERROR", "Invalid username or key.")
    ElseIf $USER_LEN < 4 Then
        MsgBox(0, "ERROR", "Invalid username or key.")
        Exit
    EndIf
    $PASS_INT = Int($USER_LEN / $PASS_LEN)
    $PASS_MOD = Mod($USER_LEN, $PASS_LEN)
    $OPKEY = _STRINGREPEAT($PASS, $PASS_INT) & StringLeft($PASS, $PASS_MOD)
    For $INDEX = 1 To $USER_LEN
        $SIG &= Chr(BitXOR(Asc(StringMid($USER, $INDEX, 1)), Asc(StringMid($OPKEY, $USER_LEN - $INDEX + 1, 1))))
    Next
    If $SIG = _STRINGREPEAT(Chr(32), $USER_LEN) Then
        MsgBox(0, "INFO", "Your key was registered.")
    Else
        MsgBox(0, "INFO", "Your key is invalid.")
    EndIf
EndFunc

Este es el resultado.

Links

Retos reversing de Challengeland.co

Introducción Recién rescatados del inframundo que es mi disco duro, os traigo un paquete de seis crackmes facilones para vuestro

Stego Ph0n3

Un error que habitualmente cometo cuando me enfrento a todo tipo de retos (especialmente en CTFs) es empezar a procesar

Migas de pan

Se nos entrega el siguiente ELF: Extracción de la Flag Si nos fijamos en las líneas 41 a la 45

Andy's Keygenme Keygen (AutoIt)

Introducción Hoy vamos a ver como extraer el script de un ejecutable compilado por Autoit, modificarlo y recompilarlo como nuestro

1 2 3 … 30 Next »

challenge challengeland challengeland.co crackme Ollydbg reto

Retos reversing de Challengeland.co

3 noviembre, 2022 por deurus·Sin comentarios

Table of Contents

Introducción

Recién rescatados del inframundo que es mi disco duro, os traigo un paquete de seis crackmes facilones para vuestro uso y disfrute. Desgraciadamente ya no está en activo la web de retos de donde los saqué así que os los dejo en descargas.

Los cuatro primero están realizados en Dev-C++ 4.9.9.2 siendo de estilo consola de comandos. Los dos restantes compilados con MingWin32 GCC 3.x carecen de GUI y vamos, que no se han esmerado mucho en darles forma.

Level 1

No cuesta mucho dar con el código interesante mediante las referencias de texto. En Ollydbg clic derecho sobre el código y Search for > All referenced text strings.

004012E1   |.  8845 E8         MOV BYTE PTR SS:[EBP-18],AL                                    ; ||||
004012E4   |.  C70424 11304000 MOV DWORD PTR SS:[ESP],level1.00403011                         ; ||||ASCII "Input Serial: "
004012EB   |.  E8 C0050000     CALL <JMP.&msvcrt.printf>                                      ; |||\printf
004012F0   |.  8D45 C8         LEA EAX,[LOCAL.14]                                             ; |||
004012F3   |.  894424 04       MOV DWORD PTR SS:[ESP+4],EAX                                   ; |||
004012F7   |.  C70424 20304000 MOV DWORD PTR SS:[ESP],level1.00403020                         ; |||ASCII "%s"
004012FE   |.  E8 9D050000     CALL <JMP.&msvcrt.scanf>                                       ; ||\scanf
00401303   |.  8D45 D8         LEA EAX,[LOCAL.10]                                             ; ||
00401306   |.  8D55 C8         LEA EDX,[LOCAL.14]                                             ; ||
00401309   |.  894424 04       MOV DWORD PTR SS:[ESP+4],EAX                                   ; ||
0040130D   |.  891424          MOV DWORD PTR SS:[ESP],EDX                                     ; ||level1.00403022
00401310   |.  E8 7B050000     CALL <JMP.&msvcrt.strcmp>                                      ; |\strcmp
00401315   |.  8945 C4         MOV [LOCAL.15],EAX                                             ; |
00401318   |.  837D C4 00      CMP [LOCAL.15],0                                               ; |
0040131C   |.  75 0E           JNZ SHORT level1.0040132C                                      ; |
0040131E   |.  C70424 23304000 MOV DWORD PTR SS:[ESP],level1.00403023                         ; |ASCII "Well done. \n"
00401325   |.  E8 86050000     CALL <JMP.&msvcrt.printf>                                      ; \printf
0040132A   |.  EB 0C           JMP SHORT level1.00401338
0040132C   |>  C70424 30304000 MOV DWORD PTR SS:[ESP],level1.00403030                         ; |ASCII "Wrong. \n"
00401333   |.  E8 78050000     CALL <JMP.&msvcrt.printf>                                      ; \printf
00401338   |>  C70424 39304000 MOV DWORD PTR SS:[ESP],level1.00403039                         ; |ASCII "PAUSE"
0040133F   |.  E8 3C050000     CALL <JMP.&msvcrt.system>                                      ; \system
00401344   |.  B8 00000000     MOV EAX,0
00401349   |.  C9              LEAVE
0040134A   \.  C3              RETN

La madre del cordero está en la dirección 401310 que es donde se lleva a cabo la función de comparación strcmp.

756296A0 msvcrt.strcmp     8B5424 04         MOV EDX,DWORD PTR SS:[ESP+4]
756296A4                   8B4C24 08         MOV ECX,DWORD PTR SS:[ESP+8] 
756296A8                   F7C2 03000000     TEST EDX,3				; 0-3 = 4 bucles. Divide la comprobación en 4 bloques
756296AE                   75 3C             JNZ SHORT msvcrt.756296EC		; salta si hemos terminado los 4 bucles
756296B0                 > 8B02              MOV EAX,DWORD PTR DS:[EDX]		; coge 4 caracteres del serial (INICIO BUCLE)
756296B2                   3A01              CMP AL,BYTE PTR DS:[ECX]		; compara el 1º/5º/9º/13º dígito en función del bucle
756296B4                   75 2E             JNZ SHORT msvcrt.756296E4		; salto a zona mala
756296B6                   0AC0              OR AL,AL
756296B8                   74 26             JE SHORT msvcrt.756296E0
756296BA                   3A61 01           CMP AH,BYTE PTR DS:[ECX+1]		; compara el 2º/6º/10º/14º dígito en función del bucle
756296BD                   75 25             JNZ SHORT msvcrt.756296E4		; salto a zona mala
756296BF                   0AE4              OR AH,AH
756296C1                   74 1D             JE SHORT msvcrt.756296E0
756296C3                   C1E8 10           SHR EAX,10
756296C6                   3A41 02           CMP AL,BYTE PTR DS:[ECX+2]		; compara el 3º/7º/11º/15º dígito en función del bucle
756296C9                   75 19             JNZ SHORT msvcrt.756296E4		; salto a zona mala
756296CB                   0AC0              OR AL,AL
756296CD                   74 11             JE SHORT msvcrt.756296E0
756296CF                   3A61 03           CMP AH,BYTE PTR DS:[ECX+3]		; compara el 4º/8º/12º/16º dígito en función del bucle
756296D2                   75 10             JNZ SHORT msvcrt.756296E4		; salto a zona mala
756296D4                   83C1 04           ADD ECX,4
756296D7                   83C2 04           ADD EDX,4
756296DA                   0AE4              OR AH,AH
756296DC                 ^ 75 D2             JNZ SHORT msvcrt.756296B0		; Si no hemos terminado... 
756296DE                   8BFF              MOV EDI,EDI                         
756296E0                   33C0              XOR EAX,EAX			; EAX = 0 que es lo deseado
756296E2                   C3                RETN				; salimos de la función superando la comprobación
756296E3                   90                NOP							
756296E4                   1BC0              SBB EAX,EAX			; Zona mala
756296E6                   D1E0              SHL EAX,1
756296E8                   83C0 01           ADD EAX,1				; EAX = 1 implica bad boy
756296EB                   C3                RETN				; salimos de la función

Si atendemos al volcado vemos el serial bueno Kcgcv8LsmV3nizfJ.

0060FEF0  31 32 33 34 35 36 37 38 39 30 00 75 40 19 18 00  1234567890.u@.
0060FF00  4B 63 67 63 76 38 4C 73 6D 56 33 6E 69 7A 66 4A  Kcgcv8LsmV3nizfJ

Curiosamente, si introducimos el serial bueno el crackme no lo acepta. Fijándome en la comprobación veo que al introducir un serial de 16 caracteres inserta un carácter nulo (0x00) alterando el serial correcto y falseando la comprobación.

0060FEF0  4B 63 67 63 76 38 4C 73 6D 56 33 6E 69 7A 66 4A  Kcgcv8LsmV3nizfJ
0060FF00  00 63 67 63 76 38 4C 73 6D 56 33 6E 69 7A 66 4A  .cgcv8LsmV3nizfJ

Ahora ya no podemos comprobarlo pero recuerdo que la web consideraba válido el serial Kcgcv8LsmV3nizfJ, por lo que considero lo anteriormente citado un bug o un intento de despiste del autor.

Level 2

Es exactamente igual que el anterior cambiando el serial por 6LPw3vDYja9KrT2V.

Level 3

La comprobación del serial es igual a las dos anteriores pero añade una función intermedia que suma 0xD a cada carácter de nuestro serial

00401355                 |.  A1 03304000     MOV EAX,DWORD PTR DS:[403003]                  ; ||
0040135A                 |.  8945 E8         MOV [LOCAL.6],EAX                              ; ||
0040135D                 |.  A1 07304000     MOV EAX,DWORD PTR DS:[403007]                  ; ||
00401362                 |.  8945 EC         MOV [LOCAL.5],EAX                              ; ||
00401365                 |.  A1 0B304000     MOV EAX,DWORD PTR DS:[40300B]                  ; ||
0040136A                 |.  8945 F0         MOV [LOCAL.4],EAX                              ; ||
0040136D                 |.  A1 0F304000     MOV EAX,DWORD PTR DS:[40300F]                  ; ||
00401372                 |.  8945 F4         MOV [LOCAL.3],EAX                              ; ||
00401375                 |.  C70424 13304000 MOV DWORD PTR SS:[ESP],level3.00403013         ; ||ASCII "Input Serial: "
0040137C                 |.  E8 CF050000     CALL <JMP.&msvcrt.printf>                      ; |\printf
00401381                 |.  8D45 D8         LEA EAX,[LOCAL.10]                             ; |
00401384                 |.  894424 04       MOV DWORD PTR SS:[ESP+4],EAX                   ; |
00401388                 |.  C70424 00304000 MOV DWORD PTR SS:[ESP],level3.00403000         ; |ASCII "%s"
0040138F                 |.  E8 AC050000     CALL <JMP.&msvcrt.scanf>                       ; \scanf
00401394                 |.  8D5D E8         LEA EBX,[LOCAL.6]
00401397                 |.  8D45 D8         LEA EAX,[LOCAL.10]
0040139A                 |.  890424          MOV DWORD PTR SS:[ESP],EAX
0040139D                 |.  E8 EEFEFFFF     CALL level3.00401290			    ; NUEVA FUNCIÓN SUMA
004013A2                 |.  895C24 04       MOV DWORD PTR SS:[ESP+4],EBX                   ; ||
004013A6                 |.  890424          MOV DWORD PTR SS:[ESP],EAX                     ; ||
004013A9                 |.  E8 82050000     CALL <JMP.&msvcrt.strcmp>                      ; |\strcmp
004013AE                 |.  8945 D4         MOV [LOCAL.11],EAX                             ; |
004013B1                 |.  837D D4 00      CMP [LOCAL.11],0                               ; |
004013B5                 |.  75 0E           JNZ SHORT level3.004013C5                      ; |
004013B7                 |.  C70424 22304000 MOV DWORD PTR SS:[ESP],level3.00403022         ; |ASCII "Well done."
004013BE                 |.  E8 8D050000     CALL <JMP.&msvcrt.printf>                      ; \printf
004013C3                 |.  EB 0C           JMP SHORT level3.004013D1
004013C5                 |>  C70424 2D304000 MOV DWORD PTR SS:[ESP],level3.0040302D         ; |ASCII "Wrong. \n"
004013CC                 |.  E8 7F050000     CALL <JMP.&msvcrt.printf>                      ; \printf
004013D1                 |>  C70424 36304000 MOV DWORD PTR SS:[ESP],level3.00403036         ; |ASCII "PAUSE"
004013D8                 |.  E8 43050000     CALL <JMP.&msvcrt.system>                      ; \system
004013DD                 |.  B8 00000000     MOV EAX,0
004013E2                 |.  8B5D FC         MOV EBX,[LOCAL.1]                              
004013E5                 |.  C9              LEAVE
004013E6                 \.  C3              RETN
--------
004012A4                 |> /8B45 08         /MOV EAX,[ARG.1]                               ; |
004012A7                 |. |890424          |MOV DWORD PTR SS:[ESP],EAX                    ; |
004012AA                 |. |E8 B1060000     |CALL <JMP.&msvcrt.strlen>                     ; \strlen
004012AF                 |. |3945 FC         |CMP [LOCAL.1],EAX
004012B2                 |. |73 1C           |JNB SHORT level3.004012D0
004012B4                 |. |8B45 08         |MOV EAX,[ARG.1]
004012B7                 |. |8B55 FC         |MOV EDX,[LOCAL.1]
004012BA                 |. |01C2            |ADD EDX,EAX
004012BC                 |. |8B45 08         |MOV EAX,[ARG.1]
004012BF                 |. |0345 FC         |ADD EAX,[LOCAL.1]
004012C2                 |. |0FB600          |MOVZX EAX,BYTE PTR DS:[EAX]
004012C5                 |. |04 0D           |ADD AL,0D					    ; char + 0xD
004012C7                 |. |8802            |MOV BYTE PTR DS:[EDX],AL
004012C9                 |. |8D45 FC         |LEA EAX,[LOCAL.1]
004012CC                 |. |FF00            |INC DWORD PTR DS:[EAX]
004012CE                 |.^\EB D4           \JMP SHORT level3.004012A4
--------
756296A0 msvcrt.strcmp     8B5424 04         MOV EDX,DWORD PTR SS:[ESP+4]
756296A4                   8B4C24 08         MOV ECX,DWORD PTR SS:[ESP+8]
756296A8                   F7C2 03000000     TEST EDX,3
756296AE                   75 3C             JNZ SHORT msvcrt.756296EC
756296B0                   8B02              MOV EAX,DWORD PTR DS:[EDX]
756296B2                   3A01              CMP AL,BYTE PTR DS:[ECX]
756296B4                   75 2E             JNZ SHORT msvcrt.756296E4
756296B6                   0AC0              OR AL,AL
756296B8                   74 26             JE SHORT msvcrt.756296E0
756296BA                   3A61 01           CMP AH,BYTE PTR DS:[ECX+1]
756296BD                   75 25             JNZ SHORT msvcrt.756296E4
756296BF                   0AE4              OR AH,AH
756296C1                   74 1D             JE SHORT msvcrt.756296E0
756296C3                   C1E8 10           SHR EAX,10
756296C6                   3A41 02           CMP AL,BYTE PTR DS:[ECX+2]
756296C9                   75 19             JNZ SHORT msvcrt.756296E4
756296CB                   0AC0              OR AL,AL
756296CD                   74 11             JE SHORT msvcrt.756296E0
756296CF                   3A61 03           CMP AH,BYTE PTR DS:[ECX+3]
756296D2                   75 10             JNZ SHORT msvcrt.756296E4
756296D4                   83C1 04           ADD ECX,4
756296D7                   83C2 04           ADD EDX,4
756296DA                   0AE4              OR AH,AH
756296DC                 ^ 75 D2             JNZ SHORT msvcrt.756296B0
756296DE                   8BFF              MOV EDI,EDI
756296E0                   33C0              XOR EAX,EAX
756296E2                   C3                RETN
756296E3                   90                NOP
756296E4                   1BC0              SBB EAX,EAX
756296E6                   D1E0              SHL EAX,1
756296E8                   83C0 01           ADD EAX,1
756296EB                   C3                RETN

En la comparación vemos que el serial bueno es AvrQQsXjDk25Jrh por lo que si restamos 0xD (13 en decimal) a cada carácter obtendremos el serial bueno.

0060FF10  41 76 72 51 51 73 58 6A 44 6B 32 35 4A 72 68 00  AvrQQsXjDk25Jrh.

		  41 76 72 51 51 73 58 6A 44 6B 32 35 4A 72 68
	                                                      - D
		  34 69 65 44 44 66 4B 5D 37 5E 25 28 3D 65 5B
		  4  i  e  D  D  f  K  ]  7  ^  %  (  =  e  [
		  
		  Serial bueno: 4ieDDfK]7^%(=e[

Level 4

La comprobación del serial es igual que la anterior pero sustituyendo la función que sumaba un valor a cada dígito del serial por una que genera un hash con nuestro serial y después lo compara con otro hash almacenado en memoria. Si no nos viene a la mente el tipo de hash que puede ser PEiD ya nos avisaba de que efectivamente el crackme incorpora la función MD5.

La función MD5 hace tiempo que no se considera segura debido a la existencia de numerosos «diccionarios» de hashes que hacen que encontremos la solución en segundos. Yo he utilizado la web MD5 online pero existen muchas más.

0060FE5C   004013BF  RETURN to level4.004013BF from <JMP.&msvcrt.strcmp>
0060FE60   0060FEA0  ASCII "e807f1fcf82d132f9bb018ca6738a19f"
0060FE64   0060FEE0  ASCII "fe01d67a002dfa0f3ac084298142eccd"


e807f1fcf82d132f9bb018ca6738a19f == 1234567890
fe01d67a002dfa0f3ac084298142eccd == orange

Level 5

La carta de presentación de este crackme es la imagen que veis arriba. Al explorarlo unos minutos enseguida nos damos cuenta de que no realiza ninguna comprobación y que nos está haciendo perder el tiempo. Ahí es cuando empezamos a revisar el ejecutable más a fondo y enseguida encontramos la solución con nuestro amigo el editor hexadecimal.

Level 6

Misma carta de presentación que el anterior y misma ausencia de comprobación del serial. En esta ocasión echando un vistazo a los recursos encontramos la solución rápidamente.

Enlaces

challenge challengeland challengeland.co crackme Ollydbg reto

Stego Ph0n3

27 abril, 2023 por deurus·Sin comentarios

Un error que habitualmente cometo cuando me enfrento a todo tipo de retos (especialmente en CTFs) es empezar a procesar el fichero proporcionado con todo tipo de herramientas como pollo sin cabeza. En el caso que nos ocupa se proporcionaba un fichero de audio WAV que procesé hasta con 4 herramientas diferentes antes de tomar aire y decidir simplemente escuchar el audio. Al escucharlo me di cuenta de que se trataba de una marcación por tonos comúnmente conocido como DTMF (Dual-Tone Multi-Frequency).

Decodificar DTMF

Con una rápida búsqueda por la web encontré una sencilla herramienta realizada en python llamada dtmf-decoder con la que enseguida obtenemos resultados. La herramienta es bastante sencilla, simplemente parte la señal en trozos, calcula la FFT (Fast Fourier Transform) para obtener las amplitudes y las compara con las de los tonos DTMF. Hay que tener en cuenta que el audio entregado es muy limpio y eso facilita mucho las cosas.

El siguiente comando nos devuelve los números marcados.

Como era de esperar, los números obtenidos no son la solución final aunque en este caso enseguida damos con que el tipo de codificación es simple y llanamente ASCII.

DTMF = 837283123119104521169510048951214811795119521101166363125
HEX  = 53 48 53 7B 77 68 34 74 5F 64 30 5F 79 30 75 5F 77 34 6E 74 3F 3F 7D
Solución: SHS{wh4t_d0_y0u_w4nt??}

challenge dtmf marcación por tonos reto

Migas de pan

4 agosto, 2024 por deurus·Sin comentarios

Se nos entrega el siguiente ELF:

/* This file was generated by the Hex-Rays decompiler version 8.4.0.240320.
   Copyright (c) 2007-2021 Hex-Rays <info@hex-rays.com>

   Detected compiler: GNU C++
*/

#include <defs.h>


//-------------------------------------------------------------------------
// Function declarations

__int64 (**init_proc())(void);
void sub_1020();
// int printf(const char *format, ...);
// int getchar(void);
// int fflush(FILE *stream);
// __int64 __isoc99_scanf(const char *, ...); weak
// void __noreturn exit(int status);
// int __fastcall _cxa_finalize(void *);
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void));
FILE **deregister_tm_clones();
__int64 register_tm_clones(); // weak
FILE **_do_global_dtors_aux();
__int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD); // weak
int __fastcall main(int argc, const char **argv, const char **envp);
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3);
void _libc_csu_fini(void); // idb
void term_proc();
// int __fastcall _libc_start_main(int (__fastcall *main)(int, char **, char **), int argc, char **ubp_av, void (*init)(void), void (*fini)(void), void (*rtld_fini)(void), void *stack_end);
// int __fastcall __cxa_finalize(void *);
// __int64 _gmon_start__(void); weak

//-------------------------------------------------------------------------
// Data declarations

_UNKNOWN _libc_csu_init;
__int64 (__fastcall *_frame_dummy_init_array_entry)() = &frame_dummy; // weak
__int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)() = &_do_global_dtors_aux; // weak
void *_dso_handle = &_dso_handle; // idb
char *a = "MdfnJk"; // weak
char *b = "jYx}"; // weak
char *c = "gWmfk"; // weak
char *d = "mlvpc"; // weak
char *f = "neU++w"; // weak
FILE *_bss_start; // idb
char completed_0; // weak


//----- (0000000000001000) ----------------------------------------------------
__int64 (**init_proc())(void)
{
  __int64 (**result)(void); // rax

  result = &_gmon_start__;
  if ( &_gmon_start__ )
    return (__int64 (**)(void))_gmon_start__();
  return result;
}
// 40D0: using guessed type __int64 _gmon_start__(void);

//----- (0000000000001020) ----------------------------------------------------
void sub_1020()
{
  JUMPOUT(0LL);
}
// 1026: control flows out of bounds to 0

//----- (0000000000001090) ----------------------------------------------------
// positive sp value has been detected, the output may be wrong!
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
  __int64 v3; // rax
  int v4; // esi
  __int64 v5; // [rsp-8h] [rbp-8h] BYREF
  char *retaddr; // [rsp+0h] [rbp+0h] BYREF

  v4 = v5;
  v5 = v3;
  _libc_start_main(
    (int (__fastcall *)(int, char **, char **))main,
    v4,
    &retaddr,
    (void (*)(void))_libc_csu_init,
    _libc_csu_fini,
    a3,
    &v5);
  __halt();
}
// 1096: positive sp value 8 has been found
// 109D: variable 'v3' is possibly undefined

//----- (00000000000010C0) ----------------------------------------------------
FILE **deregister_tm_clones()
{
  return &_bss_start;
}

//----- (00000000000010F0) ----------------------------------------------------
__int64 register_tm_clones()
{
  return 0LL;
}
// 10F0: using guessed type __int64 register_tm_clones();

//----- (0000000000001130) ----------------------------------------------------
FILE **_do_global_dtors_aux()
{
  FILE **result; // rax

  if ( !completed_0 )
  {
    if ( &__cxa_finalize )
      _cxa_finalize(_dso_handle);
    result = deregister_tm_clones();
    completed_0 = 1;
  }
  return result;
}
// 4080: using guessed type char completed_0;

//----- (0000000000001175) ----------------------------------------------------
int __fastcall main(int argc, const char **argv, const char **envp)
{
  char v4; // [rsp+7h] [rbp-9h] BYREF
  int v5; // [rsp+8h] [rbp-8h]
  bool v6; // [rsp+Fh] [rbp-1h]

  v6 = 1;
  v5 = 0;
  while ( v6 )
  {
    fflush(_bss_start);
    printf("\nIntroduce la letra correcta:\t");
    __isoc99_scanf("%c", &v4);
    getchar();
    if ( v5 > 5 )
    {
      if ( v5 > 9 )
      {
        if ( v5 > 14 )
        {
          if ( v5 > 19 )
            v6 = comprobacion(v4, f[v5 - 20], 10);
          else
            v6 = comprobacion(v4, d[v5 - 15], 2);
        }
        else
        {
          v6 = comprobacion(v4, c[v5 - 10], 8);
        }
      }
      else
      {
        v6 = comprobacion(v4, b[v5 - 6], 17);
      }
    }
    else
    {
      v6 = comprobacion(v4, a[v5], 5);
    }
    if ( !v6 )
    {
      printf("Incorrecta");
      exit(1);
    }
    printf("\n%c\n", (unsigned int)v4);
    if ( v5 == 25 )
    {
      printf("Ya tienes la flag!!");
      exit(1);
    }
    ++v5;
  }
  return 0;
}
// 1060: using guessed type __int64 __isoc99_scanf(const char *, ...);
// 4050: using guessed type char *a;
// 4058: using guessed type char *b;
// 4060: using guessed type char *c;
// 4068: using guessed type char *d;
// 4070: using guessed type char *f;

//----- (0000000000001352) ----------------------------------------------------
_BOOL8 __fastcall comprobacion(char a1, char a2, int a3)
{
  return a1 == (a3 ^ a2);
}

//----- (0000000000001390) ----------------------------------------------------
void __fastcall _libc_csu_init(unsigned int a1, __int64 a2, __int64 a3)
{
  signed __int64 v4; // rbp
  __int64 i; // rbx

  init_proc();
  v4 = &_do_global_dtors_aux_fini_array_entry - &_frame_dummy_init_array_entry;
  if ( v4 )
  {
    for ( i = 0LL; i != v4; ++i )
      ((void (__fastcall *)(_QWORD, __int64, __int64))*(&_frame_dummy_init_array_entry + i))(a1, a2, a3);
  }
}
// 1170: using guessed type __int64 __fastcall frame_dummy(_QWORD, _QWORD, _QWORD);
// 3DE8: using guessed type __int64 (__fastcall *_frame_dummy_init_array_entry)();
// 3DF0: using guessed type __int64 (__fastcall *_do_global_dtors_aux_fini_array_entry)();

//----- (00000000000013F4) ----------------------------------------------------
void term_proc()
{
  ;
}