Introducción
Aquí tenemos un crackme hecho en Java, lo que como comprobareis a continuación no es muy buena idea ya que conseguir el código fuente e incluso modificarlo no es muy dificil.
Decompilado
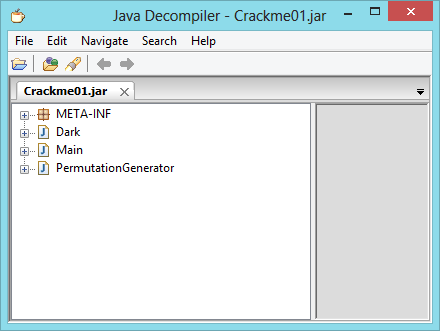
Abrimos la víctima con nuestro decompilador favorito y nos fijamos en su contenido.
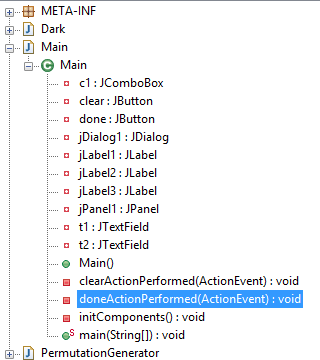
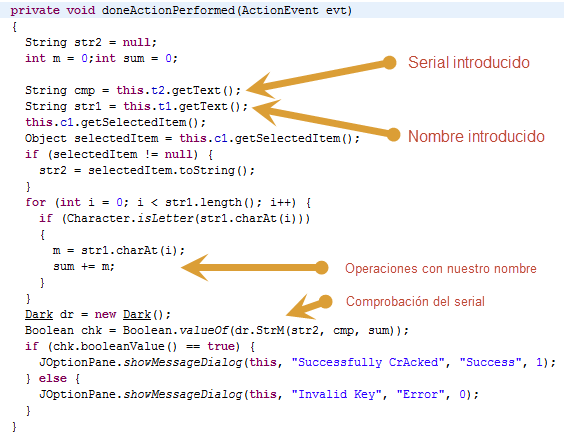
Lo interesante está en la clase Main > doneActionPerformed(ActionEvent), ya que contiene el código al ejecutar el botón que chequea el serial.
Llegados a este punto podríamos hacer cualquier cosa, parchear, que el serial válido nos lo mostrara una MessageBox etc. Pero vamos a hacer algo mejor, vamos a modificar la victima para crear nuestro keygen personalizado.
Creando un Keygen a partir de la víctima
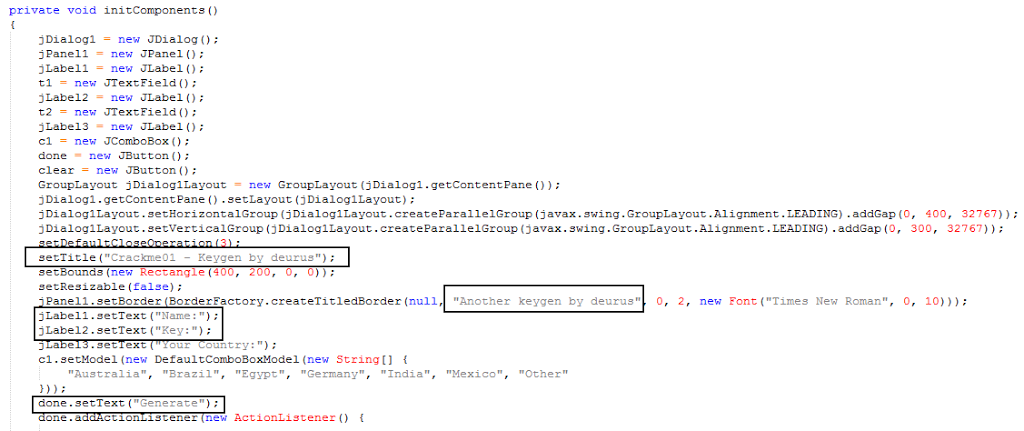
Solamente tendremos que modificar un poco la apariencia y modificar la rutina de comprobación del serial para que lo muestre en la caja de texto del serial. Finalmente abrá que recompilar.
Aquí resalto el texto a modificar para el aspecto.
Así queda la modificación para mostrar el serial correcto en la caja de texto.
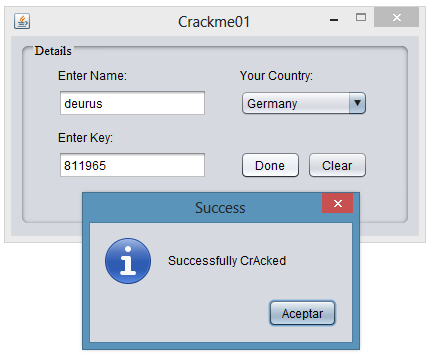
El aspecto del keygen finalmente es así.
Y como podeis apreciar funciona correctamente.