Introducción
Hoy tenemos aquí un crackme hecho en Visual Basic 6 (pcode), pero lo vamos a abordar de una manera diferente, ya que, vamos a conseguir el código fuente mediante VB Decompiler, le vamos a hacer una serie de modificaciones para hacerlo funcional con la ayuda de ExDec, y a partir de eso vamos a generar nuestro propio keygen.
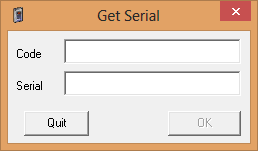
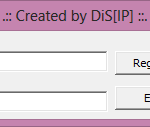
El funcionamiento del crackme es simple, tenemos una primera caja de texto «Code» que en función de lo que introduzcamos nos activa el botón «OK». Al pulsar el botón comprueba lo que tengamos en la caja de texto «Serial» para haber si está todo correcto.
Obteniendo el código fuente
Abrimos el crackme con VB Decompiler y vemos sus fauces.
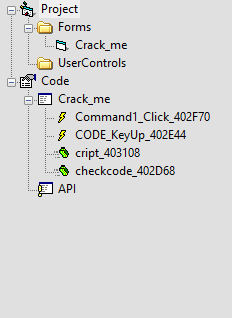
Pinchando en cada parte obtenemos su respectivo código fuente.
El botón OK
Private Sub Command1_Click() '402F70 'Data Table: 402724 Dim ourserial As Variant ourserial = CVar(Me.SERIAL.Text) 'String If (ourserial = cript(Left$(Me.CODE.Text, &HA))) Then MsgBox "Great", 0, ourserial End End If Dim x As String x = cript(Left$(Me.CODE.Text, &HA)) MsgBox "Not Completed - " & x, 0, ourserial Me.CODE.Text = "" Me.SERIAL.Text = "" Exit Sub End Sub
El evento KeyUp
Private Sub CODE_KeyUp(KeyCode As Integer, Shift As Integer) 'Data Table: 402724 If (Len(Me.CODE.Text) > 4) Then ourserialsum = checkcode(Me.CODE.Text) If CBool((ourserialsum > 70) And (ourserialsum < 90)) Then Me.Command1.Enabled = True End If End If Exit Sub End Sub
La función cript
Public Function cript(a) 'Data Table: 402724 Dim var_9C As Long var_98 = CStr(UCase(a)) For var_10C = 1 To CVar(Len(var_98)): var_CC = var_10C 'Variant var_9C = CLng((CVar(var_9C) + (CVar((Asc(Mid$(var_98, CLng(var_CC), 1)) - 9) Xor &H58) + var_CC) ^ 2)) Next var_10C 'Variant For var_160 = 1 To 100: var_140 = var_160 If (Mid$(CVar(Me.CODE.Text), CLng(var_140), 1) = vbNullString) Then GoTo loc_4030C0 End If Next var_160 loc_4030C0: var_9C = CLng(((CVar(var_9C) * Int((var_140 / 2))) * 16)) var_94 = Hex(var_9C) 'Variant cript = var_94 End Function
La función checkcode
Public Function checkcode(a) For var_F4 = 1 To CVar(Len(a)): var_A4 = var_F4 var_128 = var_128 + (CVar(Asc(Mid$(a, CLng(var_A4), 1)))) Next var_F4 var_94 = Int(((var_128 / CVar(Len(a) / CVar(Len(a))))) checkcode = var_94 End Function
La rutina de comprobación del serial
Se compone de dos partes, el código y el serial.
El código
Si el resultado de la función checkcode está entre 70 y 90 nos activa el botón OK.
El serial
Lo genera la función cript en función del código anterior.
Arreglando el código fuente
Con lo obtenido anteriormente podemos entender perfectamente el comportamiento de la comprobación del serial pero si los cargamos en Visual Basic 6 y lo intentamos ejecutar tal cual nos dará una serie de errores. Es aquí cuando entra ExDec, ya que, nos proporciona el desensamblado del programa en forma de Opcode para poder comparar con el código obtenido.
En este caso el único problema se encuentra en la función checkcode en concreto en ésta línea:
var_94 = Int(((var_128 / CVar(Len(a) / CVar(Len(a)))))
El problema está en que divide dos veces entre el número de dígitos de a, si lo analizamos vemos que es imposible ya que nunca nos daría un código entre 70 y 90. La corrección queda así:
var_94 = Int(((var_128 / CVar(Len(a)))))
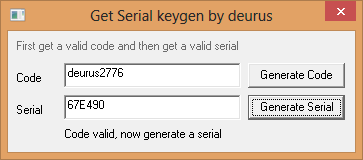
El KeyGen
Finalmente el código fuente de nuestro keygen quedaría así:
Private Sub Command1_Click() 'Generate CODE
Dim CODE As String
Dim var As Integer
Randomize
var = CLng((0 - 9999) * Rnd + 9999)
Me.CODE.Text = "deurus" & var
codesum = checkcode(Me.CODE.Text)
If CBool((codesum > 70) And (codesum < 90)) Then
lbl.Caption = "Code valid, now generate a serial"
Command2.Enabled = True
Else
Command2.Enabled = False
Command1_Click
End If
End Sub
Private Sub Command2_Click() 'Generate SERIAL
If (Len(Me.CODE.Text) > 4) Then
codesum = checkcode(Me.CODE.Text)
If CBool((codesum > 70) And (codesum < 90)) Then
SERIAL.Text = cript(Left$(Me.CODE.Text, 10))
Else
lbl.Caption = "Code not valid, first gen code"
End If
End If
End Sub
Private Sub CODE_KeyUp(KeyCode As Integer, Shift As Integer)
If (Len(Me.CODE.Text) > 4) Then
var_B0 = checkcode(Me.CODE.Text)
lbl.Caption = "Value must be between 70 - 90. Yours: " & var_B0
If CBool((var_B0 > 70) And (var_B0 < 90)) Then
lbl.Caption = "Code valid, now generate a serial"
Command2.Enabled = True
Else
Command2.Enabled = False
End If
End If
Exit Sub
End Sub
Public Function cript(a)
Dim var_9C As Long
var_98 = CStr(UCase(a))
For var_10C = 1 To CVar(Len(var_98)): var_CC = var_10C
var_9C = CLng((CVar(var_9C) + (CVar((Asc(Mid$(var_98, CLng(var_CC), 1)) - 9) Xor &H58) + var_CC) ^ 2))
Next var_10C
For var_160 = 1 To 100: var_140 = var_160
If (Mid$(CVar(Me.CODE.Text), CLng(var_140), 1) = vbNullString) Then
GoTo loc_4030C0
End If
Next var_160
loc_4030C0:
var_9C = CLng(((CVar(var_9C) * Int((var_140 / 2))) * 16))
var_94 = Hex(var_9C)
cript = var_94
End Function
Public Function checkcode(a)
For var_F4 = 1 To CVar(Len(a)): var_A4 = var_F4
'Suma el valor ascii de todos los caracteres / Add the ascii value of our code
var_128 = var_128 + (CVar(Asc(Mid$(a, CLng(var_A4), 1))))
Next var_F4
'Lo divide entre la longitud del code / Divide our codesum by code lenght
var_94 = Int(((var_128 / CVar(Len(a))))) 'corrección
checkcode = var_94
End Function
En crackmes.de podéis conseguir el crackme y el keygen.